Comparative Analysis of Enzyme Inhibition Constants: Methods, Applications, and Best Practices in Drug Discovery

Abstract

This article provides a comprehensive comparative analysis of enzyme inhibition constants (Ki, IC50), which are critical parameters in enzymology and drug development. Tailored for researchers, scientists, and drug development professionals, it covers the foundational principles of enzyme inhibition, evaluates traditional and modern methodological approaches for constant determination, addresses common troubleshooting and optimization challenges, and offers a validated comparative framework for selecting appropriate analysis techniques. By synthesizing current research and established practices, this review serves as a strategic guide for the accurate and efficient characterization of enzyme inhibitors, ultimately facilitating more robust drug discovery pipelines.

Understanding Inhibition Constants: The Bedrock of Enzymology and Therapeutic Intervention

In the fields of enzymology, drug discovery, and pharmacology, accurately quantifying the potency of inhibitory substances is fundamental for comparing compounds, predicting in vivo behavior, and guiding the development of new therapeutics. Two parameters, the inhibition constant (Ki) and the half-maximal inhibitory concentration (IC50), are cornerstone metrics used for this purpose. Although sometimes used interchangeably by those less familiar with enzyme kinetics, they represent distinct concepts with different theoretical foundations and practical implications. Ki is defined as the dissociation constant describing the binding affinity between the inhibitor and the enzyme, an intrinsic value that reflects the strength of the enzyme-inhibitor interaction independent of assay conditions. In contrast, IC50 is defined as the total concentration of inhibitor required to reduce the enzymatic activity to half of the uninhibited value in a specific assay, an operational parameter whose value is highly dependent on the experimental setup. This guide provides a comparative analysis of Ki and IC50, detailing their definitions, mathematical relationships, appropriate usage, and methodologies for estimation to support researchers in making informed decisions in their experimental design and data interpretation.

Theoretical Foundations and Definitions

Ki: The Inhibition Constant

The inhibition constant, Ki, is a thermodynamic parameter that represents the intrinsic binding affinity of an inhibitor for its enzyme target.

• Fundamental Nature: It is an equilibrium dissociation constant. For a simple competitive inhibition scenario, the equilibrium is represented as Enzyme + Inhibitor ⇌ Enzyme-Inhibitor Complex, and Ki is defined as Ki = [E][I] / [EI], where [E] is the free enzyme concentration, [I] is the free inhibitor concentration, and [EI] is the concentration of the enzyme-inhibitor complex. A lower Ki value indicates a tighter binding interaction and greater inhibitor potency.
• Mechanistic Insight: The specific interpretation of Ki can depend on the mechanism of inhibition (e.g., competitive, uncompetitive, non-competitive, mixed). For instance, in mixed inhibition, two constants, Kic and Kiu, describe the dissociation of the inhibitor from the free enzyme and the enzyme-substrate complex, respectively. The relative magnitude of these constants reveals the inhibition mechanism.
• Independence: As an intrinsic measure of affinity, Ki is, in theory, independent of enzyme concentration and, for a given inhibition mechanism, is also independent of substrate concentration.

IC50: The Half-Maximal Inhibitory Concentration

The IC50 is a functional measure of inhibitor potency derived directly from dose-response experiments.

• Fundamental Nature: It is an operational parameter indicating the total concentration of inhibitor ([I]T) required to reduce the enzymatic activity to 50% of its uninhibited value under a specific set of assay conditions. It is always measured relative to a defined system and baseline.
• Context Dependence: Unlike Ki, the IC50 value is highly dependent on the experimental conditions, including the substrate concentration, the enzyme concentration, and the incubation time. Consequently, an IC50 value is only directly comparable to other values obtained under identical conditions.
• Empirical Utility: Its key advantage is the simplicity of its determination. It does not require prior knowledge of the inhibition mechanism and can be obtained from a single dose-response curve at a fixed substrate concentration, making it a convenient first-pass metric for comparing compound potency in high-throughput screening campaigns.

Comparative Analysis: Ki vs. IC50

The following table summarizes the core differences between Ki and IC50 to facilitate a clear, objective comparison.

Table 1: Fundamental differences between Ki and IC50

Feature	Ki (Inhibition Constant)	IC50 (Half-Maximal Inhibitory Concentration)
Definition	Dissociation constant for enzyme-inhibitor binding [1]	Functional concentration for 50% activity reduction [1]
Fundamental Nature	Intrinsic measure of binding affinity [1]	Empirical, operational measure of potency [2]
Dependence on [Enzyme]	Independent (theoretically) [1]	Dependent; IC50 always larger than Ki and increases with [Enzyme] [1]
Dependence on [Substrate]	Independent for a given mechanism (but value signifies mechanism) [3]	Highly dependent; varies with [Substrate] and inhibition mechanism [2] [4]
Quantitative Relationship	Ki = IC50 / (1 + [S]/Km) for competitive inhibition (Cheng-Prusoff) [4]	IC50 = Ki (1 + [S]/Km) for competitive inhibition [2]
Theoretical Basis	Derived from enzyme kinetic theory and fitting to kinetic models [3]	Directly read from a dose-response curve [2]
Reported Value	"Free" inhibitor concentration at half-saturation [1]	"Total" inhibitor concentration for half-maximal effect [1]
Primary Application	Mechanistic studies, in vitro-in vivo extrapolation (IVIVE) [3]	Initial compound screening, functional potency ranking [2]

The relationship IC50 = E/2 + Ki, as noted in the search results, explicitly shows the dependency of IC50 on total enzyme concentration ([E]T), explaining why IC50 is always larger than Ki. This is a critical consideration when enzyme concentrations are high, particularly for tight-binding inhibitors where Ki is less than the total enzyme concentration.

Mathematical Relationships and Conversion

The most renowned framework for connecting IC50 and Ki is the Cheng-Prusoff equation. This set of relationships allows for the estimation of the intrinsic Ki from an experimentally determined IC50, provided the assay conditions and inhibition mechanism are known.

Table 2: IC50 to Ki conversion equations for major inhibition types

Inhibition Mechanism	Relationship (Ki =)	Key Dependence
Competitive	IC50 / (1 + [S]/Km) [4] [5]	Increases with higher [S]
Non-Competitive	IC50 [6]	Independent of [S]
Uncompetitive	IC50 / (1 + [S]/Km)	Decreases with higher [S]

A large-scale retrospective analysis of 343 experiments found that under specific, optimized conditions ([S] = Km, low enzyme concentration, short incubation), the Ki for competitive inhibitors could be reliably estimated as IC50/2, with 92% of predicted values falling within a 2-fold range of the experimentally determined Ki. However, for non-competitive inhibitors, this simple relationship overestimated Ki by a factor of nearly two, consistent with the theoretical expectation that Ki = IC50 for this mechanism.

Workflow for Estimation and Conversion

The following diagram illustrates the key experimental and computational pathways for determining Ki and IC50, highlighting both traditional and modern approaches.

Figure 1. A workflow comparing experimental pathways for determining IC50, traditional Ki, and the modern 50-BOA method for Ki estimation.

Experimental Protocols and Methodologies

Canonical Protocol for Ki Determination

The traditional method for determining Ki involves a comprehensive set of initial reaction velocity measurements across a matrix of substrate and inhibitor concentrations.

• Preliminary IC50 Estimation: First, a dose-response curve is generated by measuring enzyme activity over a range of inhibitor concentrations at a single substrate concentration, typically the Km value. This curve is fit to a logistic function to determine an approximate IC50 value [3].
• Establishing Experimental Matrix: Based on the estimated IC50, a full experimental design is established. This typically uses substrate concentrations at 0.2Km, Km, and 5Km, and inhibitor concentrations at 0, (1/3)IC50, IC50, and 3IC50 [3].
• Initial Velocity Measurements: The initial velocity (V0) of the enzyme-catalyzed reaction is measured for every combination of substrate and inhibitor concentrations in the matrix.
• Model Fitting and Constant Estimation: The collective velocity data is fitted to the appropriate inhibition model (e.g., the mixed inhibition model defined in the introduction, which is a general case) using non-linear regression analysis. The fitting procedure directly yields estimates for the kinetic constants, including Vmax, Km, and the inhibition constants Ki (and Kiu for mixed inhibition).

The IC50-Based Optimal Approach (50-BOA)

Recent research has demonstrated a more efficient methodology that substantially reduces the number of required experiments while maintaining precision.

• Determine IC50: As in the canonical protocol, first determine the IC50 value using a dose-response curve at a single substrate concentration (e.g., [S] = Km) [3].
• Single Inhibitor Concentration Experiment: Instead of a full matrix, perform initial velocity measurements varying the substrate concentration, but using only a single inhibitor concentration that is greater than the determined IC50.
• Integrated Fitting: Incorporate the known relationship between IC50 and the inhibition constants (Ki and Kiu) directly into the fitting process of the kinetic model to the data. This integration dramatically improves the precision of the estimation even with the drastically reduced dataset.
• Output: This approach, termed the 50-BOA (IC50-Based Optimal Approach), has been shown to reduce the number of required experiments by over 75% while ensuring accuracy and precision comparable to or better than the canonical approach [3].

Table 3: Key research reagent solutions for enzyme inhibition studies

Reagent / Solution	Function in Inhibition Assays
Recombinant Enzyme / Cell Lysate	The primary catalytic target whose activity is being measured and inhibited.
Inhibitor Compound(s)	The molecules being tested for their ability to reduce enzyme activity.
Enzyme-Specific Substrate	The molecule converted by the enzyme to product; its concentration is a key variable.
Detection Reagents (e.g., NADPH, Chromogenic Probes)	Enable quantification of reaction velocity by measuring product formation or substrate depletion.
IC50-to-Ki Converter Tools	Web servers and software that estimate Ki from IC50 using the Cheng-Prusoff equation and its derivatives, accounting for mechanism and concentrations [7].

Ki and IC50 are complementary yet distinct parameters, each with its own strategic value in the drug development pipeline. IC50 is an invaluable tool for the high-throughput screening of compound libraries, providing a rapid, mechanism-agnostic ranking of functional potency under standardized assay conditions. Its condition-dependence, however, limits its use for predictive biology. Ki, as an intrinsic binding constant, is the superior parameter for mechanistic studies, understanding the nature of enzyme-inhibitor interactions, and for in vitro-in vivo extrapolation (IVIVE) in pharmacokinetic and toxicokinetic modeling, as its value is more transferable across systems.

The choice between focusing on Ki or IC50 should be guided by the research objective: use IC50 for rapid potency ranking and Ki for deep mechanistic understanding and predictive modeling. Furthermore, the adoption of modern efficient methods like the 50-BOA can significantly accelerate the drug discovery process by providing precise Ki estimates with a fraction of the experimental effort traditionally required.

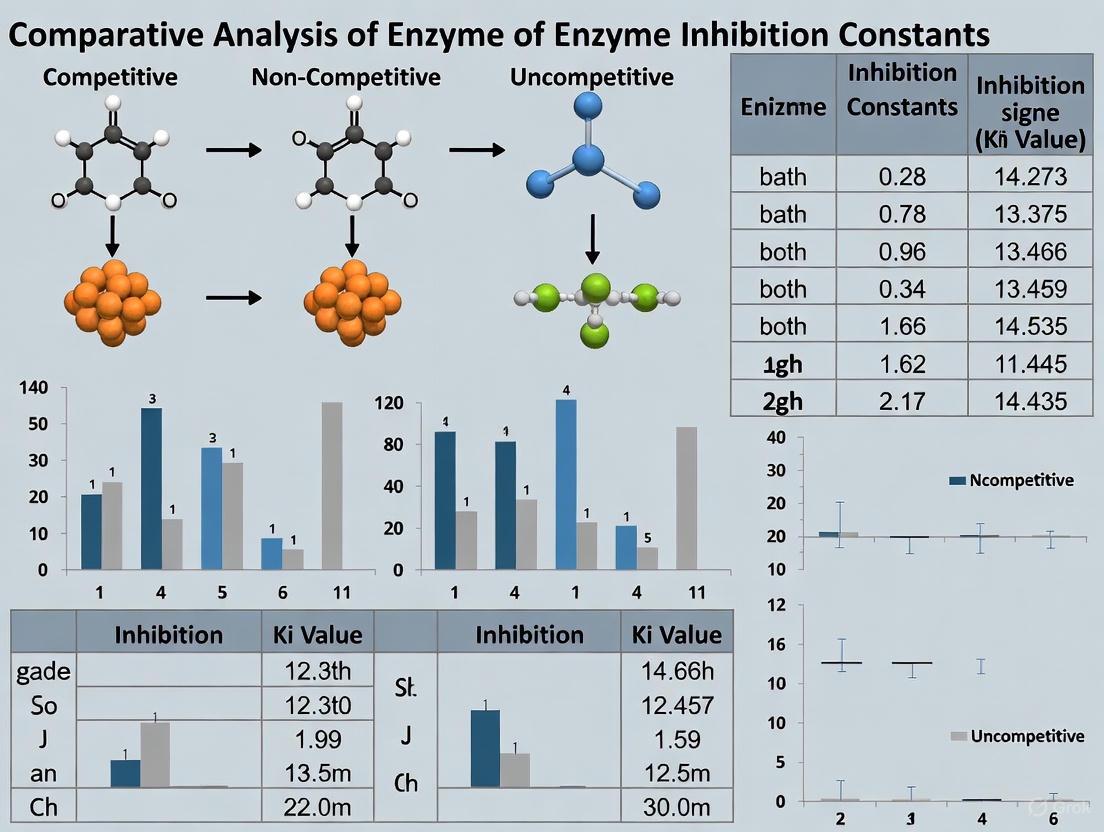
Enzyme inhibition analysis is a cornerstone of drug development and metabolic research, providing critical insights for predicting drug-drug interactions and designing therapeutic agents. The classification of reversible inhibition mechanisms—competitive, non-competitive, uncompetitive, and mixed—relies on distinct kinetic parameters that describe the interaction between an enzyme, its substrate, and an inhibitor. These parameters, specifically the inhibition constants, define the potency and mechanism of inhibition, guiding researchers in understanding biological regulation and developing targeted pharmaceuticals. This guide provides a comparative analysis of these mechanisms, supported by experimental data and methodologies relevant to researchers and drug development professionals.

Comparative Analysis of Inhibition Mechanisms

The table below summarizes the core characteristics, kinetic effects, and biological examples of the four primary reversible enzyme inhibition mechanisms.

Inhibition Type	Binding Site of Inhibitor	Effect on Km	Effect on Vmax	Inhibition Constant	Biological/Clinical Example
Competitive	Binds to the free enzyme (E) at the active site, competing with the substrate [8] [9].	Increases (Kmapp = Km(1+[I]/Kic)) [8] [9].	No change [8] [10].	Kic (slope inhibition constant) [8].	Methotrexate binds to dihydrofolate reductase, competing with folate; used in chemotherapy [10] [9].
Non-competitive	Binds to both the free enzyme (E) and the enzyme-substrate complex (ES) at an allosteric site with equal affinity [11] [12].	No change [11] [12].	Decreases (Vmaxapp = Vmax/(1+[I]/Ki)) [11] [13].	Ki (Kic = Kiu) [11] [12].	Cyanide inhibits cytochrome c oxidase; heavy metals like lead and cadmium inhibit various vital enzymes [11].
Uncompetitive	Binds exclusively to the enzyme-substrate complex (ES) [3] [14].	Decreases [3].	Decreases [3].	Kiu (intercept inhibition constant) [3].	ECSI#6 inhibits the serotonin transporter (SERT) by preferentially binding to its inward-facing, potassium-bound conformation [14].
Mixed	Binds to both the free enzyme (E) and the enzyme-substrate complex (ES), but with different affinities [15] [3].	Increases or decreases [15].	Decreases [15].	Kic and Kiu (Kic ≠ Kiu) [15] [3].	Often a result of active-site binding in multi-substrate reactions or tight-binding inhibitors, rather than binding to two distinct sites [15].

Experimental Protocols for Inhibition Studies

Accurate determination of inhibition mechanisms relies on well-established kinetic experiments. The following protocol details the canonical method for characterizing inhibition.

Canonical Enzyme Inhibition Assay

This protocol is used to determine the type of inhibition and calculate the inhibition constants (Kic and Kiu) by measuring initial reaction velocities under varying conditions [3].

1. Reagent Preparation:

• Enzyme Solution: Prepare a stock solution of the purified enzyme in an appropriate buffer. Keep on ice to maintain stability.
• Substrate Stock Solution: Prepare a concentrated stock solution of the substrate.
• Inhibitor Stock Solutions: Prepare serial dilutions of the inhibitor to achieve a range of concentrations, typically centered around the IC50 value.
• Reaction Buffer: Use a buffer that maintains optimal pH and ionic strength for the enzyme, and includes any necessary cofactors.

2. IC50 Determination (Initial Scoping):

• Measure the initial velocity of the enzyme reaction at a single substrate concentration (often near the Km) across a broad range of inhibitor concentrations [3].
• Plot the percentage of control activity (without inhibitor) versus the logarithm of inhibitor concentration ([I]).
• Fit a dose-response curve to the data to determine the IC50 value—the concentration of inhibitor that reduces enzyme activity by 50% under these specific conditions [3].

3. Comprehensive Kinetic Data Collection:

• Design an experiment that measures initial reaction rates using a matrix of substrate and inhibitor concentrations.
• Substrate Concentrations: Use a range that brackets the Km (e.g., 0.2Km, Km, and 5Km) [3].
• Inhibitor Concentrations: Use a range based on the estimated IC50 (e.g., 0, â…“ IC50, IC50, and 3 IC50) [3].
• For each combination, initiate the reaction by adding the enzyme, allow it to proceed for a set time within the linear range, and then stop it.
• Quantify the product formed or substrate consumed using spectroscopic, chromatographic, or other suitable methods.

4. Data Analysis and Model Fitting:

• Plot the data on a Lineweaver-Burk (double-reciprocal) plot (1/v vs. 1/[S]) for each inhibitor concentration.
• The pattern of lines indicates the inhibition type: competitive lines intersect on the y-axis; non-competitive lines intersect on the x-axis; uncompetitive lines are parallel; and mixed inhibition lines intersect in the second quadrant [8] [11].
• Fit the initial velocity data directly to the general mixed inhibition equation using nonlinear regression software to obtain the most accurate estimates for Vmax, Km, Kic, and Kiu [3]: Vâ‚€ = (Vmax × [S]) / ( Km × (1 + [I]/Kic) + [S] × (1 + [I]/Kiu) )

Note on Advanced Methods: Recent studies suggest that precise estimation of inhibition constants, even for the mixed model, can be achieved with a drastically reduced dataset. The 50-BOA (IC50-Based Optimal Approach) uses a single inhibitor concentration greater than the IC50, incorporated into the fitting process, to reliably estimate Kic and Kiu with >75% fewer experiments [3].

Visualization of Inhibition Mechanisms and Workflows

The following diagrams illustrate the molecular mechanisms and experimental workflows for enzyme inhibition analysis.

Mechanism of Reversible Enzyme Inhibition

Enzyme Inhibition Assay Workflow

The Scientist's Toolkit: Research Reagent Solutions

The table below lists key reagents and materials essential for conducting enzyme inhibition experiments.

Research Reagent/Material	Function in Inhibition Studies
Purified Target Enzyme	The protein whose activity is being measured and inhibited. Purity is critical for accurate kinetic analysis.
Enzyme Substrate	The molecule converted to product by the enzyme. Used at varying concentrations to determine kinetic parameters.
Inhibitor Compounds	Molecules tested for their ability to reduce enzyme activity. Stock solutions are prepared at high concentration for serial dilution.
Reaction Buffer	Aqueous solution that maintains optimal pH, ionic strength, and provides necessary cofactors (e.g., Mg²⁺, NADPH) for enzyme function.
Microplate Reader / Spectrophotometer	Instrument for high-throughput measurement of product formation or substrate consumption, often via absorbance or fluorescence.
Analytical Software	Non-linear regression tools (e.g., GraphPad Prism, R, MATLAB) for fitting data to kinetic models and estimating parameters like Ki and IC50 [3] [13].
Parasin I	Parasin I, MF:C82H154N34O24, MW:2000.3 g/mol
Pirimicarb-d6	Pirimicarb-d6, CAS:1015854-66-6, MF:C11H18N4O2, MW:244.32 g/mol

The classification of enzyme inhibition mechanisms through kinetic analysis remains a fundamental practice in biochemical research and pharmaceutical development. Competitive inhibition is characterized by an increased apparent Km without affecting Vmax, while non-competitive inhibition reduces Vmax leaving Km unchanged. Uncompetitive inhibition, which is relatively rare, uniquely decreases both Km and Vmax. Mixed inhibition presents a more complex picture, often involving alterations to both parameters. Emerging methodologies, such as the 50-BOA, are refining the efficiency of these studies, enabling precise estimation of inhibition constants with reduced experimental burden. A clear understanding of these principles and techniques is indispensable for researchers aiming to elucidate metabolic pathways, design effective drugs, and anticipate clinical drug interactions.

In drug discovery and biochemical research, accurately quantifying a molecule's ability to inhibit an enzyme is fundamental. Two parameters stand as critical metrics for this assessment: the half-maximal inhibitory concentration (IC50) and the inhibition constant (Ki). While often discussed interchangeably, they represent fundamentally different concepts. The IC50 is an experimentally derived concentration that depends heavily on specific assay conditions, whereas the Ki is an absolute thermodynamic constant representing the true binding affinity between an inhibitor and its enzyme target [16]. This guide provides a comparative analysis of these two key parameters, focusing on the theoretical and practical application of the Cheng-Prusoff equation, which serves as the crucial link between empirical measurement (IC50) and fundamental biochemical property (Ki).

The central challenge in comparing inhibitor potency arises from the condition-dependent nature of IC50 values. As a direct consequence of this relationship, IC50 values obtained under different substrate concentrations cannot be directly compared, whereas Ki values, being intrinsic properties, provide a standardized basis for comparison across different experimental setups and studies [16]. This distinction is not merely academic; it has profound implications for the reliability of data interpretation in drug development pipelines.

Theoretical Foundation: Ki vs. IC50

Comparative Definitions and Properties

The following table summarizes the core characteristics of Ki and IC50, highlighting their comparative differences.

Table 1: Fundamental Comparison between IC50 and Ki

Feature	IC50	Ki
Definition	Concentration of inhibitor that reduces enzyme activity by 50% under a specific set of assay conditions [16]	Equilibrium dissociation constant for the enzyme-inhibitor complex; concentration at which 50% of enzyme sites are occupied in the absence of substrate [16]
Dependence on Substrate Concentration	Yes, significantly affected by [S] and Km [16] [10]	No, an intrinsic property of the enzyme-inhibitor interaction [16]
Nature	Empirical measurement	Fundamental thermodynamic constant
Comparability	Can only be compared when measured under identical conditions [16]	Can be compared across different studies and experimental setups [16]
Primary Use	Initial, experimental readout of inhibitor potency	Gold-standard metric for reporting binding affinity and inhibitor potency

The Cheng-Prusoff Relationship

The mathematical relationship that connects IC50 to Ki for competitive inhibition is defined by the Cheng-Prusoff equation [16] [5] [17]:

Ki = IC50 / (1 + [S]/Km)

In this equation:

• Ki is the inhibition constant.
• IC50 is the half-maximal inhibitory concentration measured experimentally.
• [S] is the concentration of the substrate used in the assay.
• Km is the Michaelis-Menten constant of the substrate for the enzyme [16].

This equation illustrates a critical concept: the measured IC50 is always greater than the true Ki, and the difference is a function of how closely the substrate concentration [S] approaches the enzyme's Km. When [S] is much lower than Km, the IC50 approaches the Ki value. Conversely, as [S] increases, the IC50 value becomes progressively larger than the Ki [16] [10]. The equation can be rearranged to predict an IC50 from a known Ki: IC50 = Ki × (1 + [S]/Km) [17].

Figure 1: The workflow for converting the empirical IC50 value into the fundamental Ki constant using the Cheng-Prusoff equation, which requires knowledge of the assay's substrate concentration ([S]) and the enzyme's Km for the substrate.

Experimental Protocols for Determination

Accurate determination of Ki via the Cheng-Prusoff equation relies on robust experimental protocols for obtaining its components: IC50, Km, and [S].

The Canonical IC50 Determination Protocol

The traditional method for estimating inhibition constants is a multi-step process that ensures reliable data collection [3].

• Preliminary IC50 Estimation:

  • The % control activity of the enzyme is measured over a range of inhibitor concentrations ([I]).
  • A single substrate concentration is used, typically set at or near the Km value for that substrate [3].
  • A dose-response curve is fitted to the data to determine the preliminary IC50 value.

• Establishing the Experimental Design:

  • A matrix of experimental conditions is established based on the preliminary IC50.
  • Substrate Concentrations ([S]): Typically tested at 0.2 Km, Km, and 5 Km to characterize the inhibition mechanism and potency across different saturation levels [3].
  • Inhibitor Concentrations ([I]): Typically tested at 0, (1/3) IC50, IC50, and 3 × IC50 to adequately define the inhibition curve [3].
  • For each combination of [S] and [I], the initial velocity (V0) of the enzyme reaction is measured.

• Data Fitting and Constant Estimation:

  • The initial velocity data is fitted to the appropriate inhibition model (e.g., competitive, mixed) to estimate the inhibition constants Kic and Kiu [3].
  • The general equation for mixed inhibition is: V0 = (Vmax * [S]) / ( Km * (1 + [I]/Kic ) + [S] * (1 + [I]/Kiu) ) [3].

Advanced and Rapid Methodologies

Recent methodological advances are streamlining the process of inhibition constant determination.

• The 50-BOA (IC50-Based Optimal Approach): A 2025 study demonstrates that precise and accurate estimation of inhibition constants is possible using a single inhibitor concentration greater than the IC50, a significant reduction from traditional methods. This approach incorporates the relationship between IC50 and the inhibition constants directly into the fitting process, reducing the number of required experiments by over 75% while maintaining precision [3].

• One-Step Capillary Electrophoresis (CE): An improved capillary electrophoresis method allows for the rapid, one-step determination of both enzyme kinetic constants (Km, Vmax) and inhibition constants. This technique uniquely integrates reactant mixing, enzymatic reaction, and product separation within a single capillary. A key feature is "zero-volume change mixing," which allows for the analysis of the dynamic enzymatic reaction process and subsequent extraction of kinetic parameters from the product peak profile on the electropherogram [18].

The Scientist's Toolkit: Essential Research Reagents and Materials

Successful execution of enzyme inhibition assays requires specific, high-quality reagents and materials. The following table details key solutions and their critical functions in the experimental workflow.

Table 2: Essential Research Reagents and Materials for Enzyme Inhibition Assays

Reagent/Material	Function in Inhibition Assays
Pooled Human Liver Microsomes (HLM)	A common enzyme source for studying the inhibition of human drug-metabolizing enzymes, particularly Cytochrome P450s (CYPs) [19].
Recombinant Enzymes	Provide a pure system for studying inhibition against a specific enzyme target without interference from other enzymatic activities.
Cytochrome P450 Probe Substrates (e.g., Midazolam for CYP3A4)	Specific substrates metabolized by a single CYP enzyme, allowing for targeted inhibition studies [19].
β-Nicotinamide Adenine Dinucleotide Phosphate (NADPH)	Essential cofactor for CYP-mediated and other oxidative metabolism; required as an electron donor in reaction mixtures [19].
Inactivation Co-factors (e.g., Glutathione, GSH)	Used as trapping agents in time-dependent inhibition (TDI) assays to bind reactive intermediate metabolites and provide a more physiologically relevant assessment [19].
Capillary Electrophoresis (CE) System	Used in advanced methods for integrated on-line enzymatic reaction, separation, and detection, minimizing sample consumption and analysis time [18].
Sulfaguanidine	Sulfaguanidine, CAS:6190-55-2, MF:C7H10N4O2S, MW:214.25 g/mol
Rhamnose monohydrate	Rhamnose monohydrate, CAS:6155-35-7, MF:C6H12O5.H2O, MW:182.17 g/mol

Critical Considerations and Modern Perspectives

Limitations and Appropriate Use of the Cheng-Prusoff Equation

The Cheng-Prusoff equation is a powerful tool but has specific limitations that researchers must acknowledge.

• Valid for Reversible Inhibition: The relationship assumes a reversible, equilibrium-based interaction between the enzyme and inhibitor [16].
• Assumes No Cooperativity: The model assumes simple bimolecular interaction kinetics without cooperativity between binding sites [16] [5].
• Inhibition Mechanism Specificity: The standard equation Ki = IC50 / (1 + [S]/Km) is explicitly derived for competitive inhibition [16] [17] [10]. Different forms of the equation apply to other mechanisms:
  • For non-competitive inhibition, Ki = IC50, as the IC50 is theoretically independent of substrate concentration [10].
  • For uncompetitive inhibition, the relationship is Ki = IC50 / (1 - [S]/Km), which is less commonly encountered [3].
• Power Equations for Complex Systems: In functional assays (e.g., cellular or tissue responses), agonist-receptor interactions may not follow simple kinetics. A more general power equation has been derived to account for cooperativity: KB = IC50 / (1 + (A/EC50)^K ), where K is a slope function representing overall cooperativity influences [5].

Impact of Experimental Design on Data Quality

The precision of estimated inhibition constants is highly sensitive to experimental design choices. A 2025 analysis of the "error landscape" for estimation revealed that nearly half of the data points collected in conventional experimental designs may be dispensable and can even introduce bias [3]. The study found that data obtained using low total inhibitor concentrations ([I]T) provides little information for the precise estimation of inhibition constants, especially for the Kiu parameter in mixed inhibition models. This insight directly challenges traditional protocols and underscores the superiority of modern, optimized approaches like the 50-BOA, which uses a single, well-chosen inhibitor concentration to achieve higher precision with far fewer experiments [3].

Figure 2: The logical relationship between substrate concentration [S], the measured IC50, and the true Ki. High [S] leads to a large overestimation of the inhibitor's true affinity (higher IC50), while low [S] yields an IC50 closer to the Ki, which the Cheng-Prusoff equation corrects for in both cases.

The Role of Inhibition Constants in Target Validation and Druggability Assessment

In the disciplined world of drug development, the journey from a theoretical target to a viable therapeutic candidate is paved with quantitative rigor. At the heart of this process lies the critical evaluation of enzyme inhibitors, where the inhibition constant (Ki) serves as a fundamental metric for assessing both the potency of a drug candidate and the druggability of its intended target. This guide provides a comparative analysis of the key experimental methodologies used to determine these essential parameters, offering researchers a framework for robust target validation.

Fundamental Concepts of Enzyme Inhibition

Enzyme-catalyzed reactions can be suppressed by an inhibitor (I) that binds to either the free enzyme (E) or the enzyme-substrate complex (C), forming reversible complexes with dissociation constants of Kic or Kiu, respectively [3]. These inhibition constants characterize not only the potency of the inhibition—with lower constants indicating higher binding affinity—but also the mechanism of action.

The relative magnitude of these two constants determines the inhibition type: competitive (Kic << Kiu), uncompetitive (Kiu << Kic), or mixed (Kic ≈ Kiu) [3]. The initial velocity of the enzyme-catalyzed reaction (V₀) is described by a general equation that can describe all these inhibition types [3]: $$V₀ = \frac{V{max} ST}{KM (1 + \frac{IT}{K{ic}}) + ST (1 + \frac{IT}{K{iu}})}$$

Comparative Analysis of Methodologies for Determining Inhibition Constants

The following table summarizes the core characteristics, advantages, and limitations of major methodological approaches for inhibitor characterization.

Method	Key Principle	Data Output	Throughput	Key Applications	Major Strengths	Key Limitations
Classical Multi-Concentration Analysis [3]	Fitting velocity data from multiple substrate and inhibitor concentrations to kinetic models.	Ki, Vmax, KM	Low	Basic enzyme characterization; mechanistic studies.	Well-established; provides comprehensive kinetic parameters.	High reagent consumption; time-intensive; can introduce bias.
50-BOA (IC50-Based Optimal Approach) [3]	Uses relationship between IC50 and Ki with a single inhibitor concentration >IC50 for fitting.	Kic, Kiu	High (>75% reduction in experiments)	Efficient drug screening; target validation.	Dramatically reduces experimental load; maintains precision/accuracy.	Requires initial IC50 determination.
Dixon Plot [20]	Plots reciprocal velocity (1/v) against inhibitor concentration [I] at different substrate levels.	Ki (from intersection point)	Medium	Visual determination of Ki and inhibition mechanism.	Simple graphical method; clear visualization of inhibition type.	Less precise than comprehensive fitting; interpretation sensitive.
Capillary Electrophoresis (One-Step) [18]	Monitors substrate depletion/product formation as zones migrate and interact within a capillary.	Ki, KM	High	Rapid screening of inhibitors; enzyme kinetics with minimal sample.	Very low reagent consumption; automated and rapid.	Specialized equipment required; method development can be complex.
Kitz & Wilson (Continuous Progress Curves) [21]	Fits progress curves of product formation in the presence of inhibitor to a decay model.	KI, kinact	Medium	Characterization of irreversible covalent inhibitors.	Directly measures time-dependent inhibition; provides kinetic constants.	Requires continuous assay; complex fitting; prone to error with substrate depletion [22].
Time-Dependent IC50 (Reversible Covalent) [22]	Models shift in IC50 values with varying pre-incubation or incubation times.	Ki, k₅, k₆	Medium	Evaluating reversible covalent inhibitors with time-dependent effects.	Deconvolutes binding and covalent modification kinetics.	Complex modeling; requires multiple time-point experiments.

Classical Multi-Concentration Analysis

• Experimental Workflow:
  • IC50 Determination: Initially estimate the half-maximal inhibitory concentration (IC50) using a range of inhibitor concentrations at a single substrate concentration (typically at KM) [3].
  • Experimental Design: Establish a matrix of substrate concentrations (e.g., 0.2KM, KM, and 5KM) and inhibitor concentrations (e.g., 0, â…“IC50, IC50, and 3IC50) [3].
  • Data Collection: Measure the initial velocity (Vâ‚€) of the enzymatic reaction for each concentration combination.
  • Parameter Estimation: Fit the collected velocity data to the appropriate inhibition model (e.g., the general equation for mixed inhibition) using non-linear regression to estimate the inhibition constants (Kic and Kiu) [3].

50-BOA (IC50-Based Optimal Approach)

• Experimental Workflow:
  • IC50 Determination: As in the classical method, first determine the IC50 value of the inhibitor [3].
  • Optimized Experimental Design: For a single substrate concentration (e.g., at KM), use only a single inhibitor concentration that is greater than the determined IC50 value. Research indicates this single point can suffice for precise estimation [3].
  • Data Collection & Fitting: Measure the initial velocity at this condition. Crucially, incorporate the established harmonic mean relationship between the IC50 and the inhibition constants (Kic and Kiu) directly into the fitting process to estimate their values [3].

Characterization of Time-Dependent Covalent Inhibitors

• Experimental Workflow for Reversible Covalent Inhibitors [22]:
  • Time-Dependent IC50 Assay: Perform a series of IC50 determinations where the pre-incubation time (enzyme with inhibitor) or the incubation time (enzyme, inhibitor, and substrate) is systematically varied.
  • Data Analysis: Fit the resulting time-dependent IC50 data using specialized methods, such as an implicit equation or numerical modelling (e.g., EPIC-CoRe), to derive the initial non-covalent inhibition constant (Ki), the covalent modification rate constants (kâ‚… and k₆), and the overall inhibition constant (K_i^{app}) [22].

The Scientist's Toolkit: Essential Reagents and Materials

The table below outlines key reagents and materials essential for conducting robust enzyme inhibition assays.

Reagent/Material	Function in Inhibition Assays	Example Applications	Key Considerations
Purified Enzyme Target	The biological macromolecule whose function is being inhibited.	Alkaline Phosphatase, α-Glucosidase, Xanthine Oxidase [18] [23]	Purity, stability, and source (recombinant vs. native) are critical for reproducible kinetics.
Chemical Inhibitors	Compounds screened or characterized for inhibitory activity.	Saxagliptin (reversible covalent DPPIV inhibitor) [22]	Solubility (may require DMSO stocks), stability in assay buffer, and potential for non-specific binding.
Enzyme Substrate	The molecule converted by the enzyme to a detectable product.	p-Nitrophenyl-disodium phosphate for Alkaline Phosphatase [18]	Must be specific to the enzyme; product should be distinguishable from substrate for detection.
Capillary Electrophoresis System	Instrumentation for separation-based kinetic analysis [18].	One-step determination of Ki and KM [18]	Enables minimal reagent use and automated, rapid analysis.
Detection Reagents/Sensors	Enable quantification of reaction progress.	Absorbance/fluorescence probes, LC-MS detectors [21]	Compatibility with enzyme activity, sensitivity, and dynamic range must be validated.
Cetrorelix Acetate	Cetrorelix Acetate, CAS:1631741-31-5, MF:C72H96ClN17O16, MW:1491.1 g/mol	Chemical Reagent	Bench Chemicals
Diperodon Hydrochloride	Diperodon Hydrochloride, CAS:537-12-2, MF:C22H28ClN3O4, MW:433.9 g/mol	Chemical Reagent	Bench Chemicals

Experimental Workflow Visualization

The following diagram illustrates the core decision-making workflow for selecting and applying the key methodologies discussed in this guide.

Discussion and Strategic Application

The choice of methodology is not merely a technical decision but a strategic one that directly impacts the reliability and efficiency of target validation. The emerging 50-BOA method challenges the canonical requirement for extensive data collection, demonstrating that precise and accurate estimation of inhibition constants is possible with a single, well-chosen inhibitor concentration, thereby streamlining early-stage screening [3].

For covalent inhibitors, the kinetic characterization must be more nuanced. Methods that deconvolute the initial binding affinity (KI) from the rate of covalent modification (kinact for irreversible; k₅/k₆ for reversible) are essential for a true structure-activity relationship, guiding the optimization of warhead reactivity and binding scaffold selectivity [22] [21].

Ultimately, a well-determined inhibition constant (Ki) provides a foundational metric for druggability assessment. A potent Ki suggests strong target engagement potential, while the mechanism of inhibition informs on the likely pharmacological profile and potential clinical management strategies [3] [24]. Integrating these precise kinetic parameters into broader pharmacological and toxicological profiles enables researchers to make data-driven decisions on which targets and inhibitor chemotypes to advance through the costly drug development pipeline.

Methodologies for Determining Ki: From Classical Analyses to Cutting-Edge Approaches

The accurate determination of enzyme kinetics and inhibition constants is a cornerstone of biochemical research and pharmaceutical development. Classical linearization methods provide accessible graphical approaches to estimate key parameters such as the Michaelis constant (Kₘ), maximum velocity (Vₘₐₓ), and inhibition constant (Kᵢ). Among these, the Lineweaver-Burk, Eadie-Hofstee, and Dixon plots have been widely utilized for decades to transform the hyperbolic Michaelis-Menten equation into linear forms, enabling researchers to extract kinetic parameters through linear regression [25] [26].

Despite their historical significance and continued use in educational settings, these linear transformation methods exhibit significant limitations in accuracy and precision compared to modern nonlinear regression techniques [27] [25]. This comparative analysis examines the underlying principles, applications, and methodological constraints of these three classical linearization approaches, providing researchers with a framework for selecting appropriate analytical methods based on their experimental requirements and precision needs.

Theoretical Foundations and Mathematical Formulations

The Michaelis-Menten Equation

Enzyme-catalyzed reactions follow a hyperbolic relationship between substrate concentration ([S]) and initial reaction velocity (Vâ‚€), described by the Michaelis-Menten equation:

[ V0 = \frac{V{max} [S]}{K_m + [S]} ]

where Vₘₐₓ represents the maximum reaction velocity attained at infinite substrate concentration, and Kₘ is the Michaelis constant, defined as the substrate concentration at half Vₘₐₓ [28]. The Kₘ value provides insight into the enzyme's affinity for its substrate, with lower values indicating higher affinity [28].

Principles of Linear Transformation

Linear transformation methods convert this hyperbolic relationship into a linear form by applying algebraic manipulations, allowing kinetic parameters to be determined from the slopes and intercepts of straight-line plots [26]. This approach gained historical significance due to the simplicity of linear regression calculations before the widespread availability of computers capable of performing nonlinear regression [25].

Methodological Comparison of Linearization Approaches

Lineweaver-Burk Plot

The Lineweaver-Burk plot, also known as the double-reciprocal plot, transforms the Michaelis-Menten equation by taking reciprocals of both sides [25]:

[ \frac{1}{V0} = \frac{Km}{V{max}} \cdot \frac{1}{[S]} + \frac{1}{V{max}} ]

This creates a linear relationship where 1/V₀ is plotted against 1/[S], yielding a straight line with slope of Kₘ/Vₘₐₓ, y-intercept of 1/Vₘₐₓ, and x-intercept of -1/Kₘ [25] [26].

Applications and Limitations: The Lineweaver-Burk plot is particularly useful for distinguishing different types of enzyme inhibition. Competitive inhibitors increase the apparent Kₘ without affecting Vₘₐₓ, resulting in plots with different slopes that intersect on the y-axis. Uncompetitive inhibitors decrease both Kₘ and Vₘₐₓ, producing parallel lines. Non-competitive and mixed inhibitors affect both parameters, causing intersections typically in the second quadrant [25] [29].

The primary limitation of this method stems from the reciprocal transformation, which disproportionately compresses data points at high substrate concentrations while expanding those at low concentrations where measurement errors are typically larger [25]. This distortion amplifies experimental errors and can yield biased parameter estimates, making it the least accurate among linearization methods [27] [25] [26].

Eadie-Hofstee Plot

The Eadie-Hofstee plot employs an alternative linearization of the Michaelis-Menten equation:

[ V0 = V{max} - Km \cdot \frac{V0}{[S]} ]

In this approach, V₀ is plotted against V₀/[S], generating a straight line with slope of -Kₘ, y-intercept of Vₘₐₓ, and x-intercept of Vₘₐₓ/Kₘ [26].

Applications and Limitations: The Eadie-Hofstee plot offers a significant advantage over the Lineweaver-Burk method by avoiding reciprocal transformation of the measured reaction velocities, giving equal weight to all data points [26]. This provides a more reliable estimate of kinetic parameters, particularly Vₘₐₓ [26]. The plot directly displays both fundamental kinetic parameters: Vₘₐₓ (krelease) as the y-intercept and Vₘₐₓ/Kₘ (kcapture) as the x-intercept [26].

A potential limitation is that both axes contain Vâ‚€, so any experimental error in measuring velocity will affect both coordinates [26]. Nevertheless, the Eadie-Hofstee plot is generally recommended over Lineweaver-Burk for determining kinetic parameters from experimental data [26].

Dixon Plot

The Dixon plot specializes in analyzing enzyme inhibition kinetics, plotting 1/Vâ‚€ against inhibitor concentration [I] at varying substrate concentrations [30]:

[ \frac{1}{V0} = \frac{Km}{V{max}[S]}(1 + \frac{[I]}{Ki}) + \frac{1}{V_{max}} ]

The intersection point of lines obtained at different substrate concentrations provides an estimate of the inhibition constant Káµ¢, with the lines crossing at [I] = -Káµ¢ [30].

Applications and Limitations: This method is particularly valuable for distinguishing between competitive, non-competitive, and uncompetitive inhibition mechanisms and determining inhibitor potency [30] [29]. It provides a visual assessment of inhibitor strength and is foundational for pharmacological assays in drug discovery [30].

The Dixon plot shares similar limitations with other reciprocal plots regarding error distortion. Additionally, accurate determination requires testing multiple substrate concentrations to generate the intersecting lines necessary for Káµ¢ estimation [30].

Table 1: Comparative Characteristics of Classical Linearization Methods

Feature	Lineweaver-Burk	Eadie-Hofstee	Dixon
Variables Plotted	1/Vâ‚€ vs 1/[S]	Vâ‚€ vs Vâ‚€/[S]	1/Vâ‚€ vs [I]
Y-Intercept	1/Vₘₐₓ	Vₘₐₓ	Complex function of parameters
Slope	Kₘ/Vₘₐₓ	-Kₘ	Varies with inhibition type
X-Intercept	-1/Kₘ	Vₘₐₓ/Kₘ	Varies with inhibition type
Primary Application	Determining Kₘ and Vₘₐₓ	Determining Kₘ and Vₘₐₓ	Determining Kᵢ
Error Distribution	Unequal weighting, amplifies errors	Equal weighting of Vâ‚€ measurements	Unequal weighting, amplifies errors
Recommended Use	Educational demonstration, inhibition typing	Parameter estimation from experimental data	Inhibition constant determination

Experimental Protocols and Data Analysis

General Experimental Workflow for Enzyme Kinetics

Detailed Protocol for Michaelis-Menten Parameter Determination

• Enzyme Preparation: Prepare purified enzyme solution with standardized activity units. Maintain constant enzyme concentration across all assays while varying substrate concentrations [26].

• Substrate Dilution Series: Create minimum of 6-8 substrate concentrations spanning a range from below to above the expected Kₘ value (typically 0.2Kₘ to 5Kₘ) [26]. Ideally, include 3-4 concentrations below Kₘ and 3-4 above Kₘ for optimal parameter estimation [26].

• Initial Velocity Measurement: For each substrate concentration, measure the initial rate of product formation (Vâ‚€) by monitoring the linear phase of the reaction. Ensure less than 10% substrate depletion during the measurement period to maintain steady-state conditions [31] [26].

• Data Transformation and Plotting:

  • Lineweaver-Burk: Calculate 1/Vâ‚€ and 1/[S] for each data point [25] [26].
  • Eadie-Hofstee: Calculate Vâ‚€/[S] for each data point [26].
  • Direct Linear Plot: Plot each [S] on the negative x-axis and corresponding Vâ‚€ on the y-axis, drawing lines between them; the intersection point estimates (Kₘ, Vₘₐₓ) [26].

• Parameter Estimation: Perform linear regression on transformed data. For Lineweaver-Burk: Vₘₐₓ = 1/y-intercept, Kₘ = slope/y-intercept. For Eadie-Hofstee: Vₘₐₓ = y-intercept, Kₘ = -slope [26].

Protocol for Inhibition Constant Determination Using Dixon Plot

• Experimental Design: Select 3-4 substrate concentrations (typically 0.5Kₘ, 1Kₘ, and 2Kₘ) and 5-6 inhibitor concentrations including 0 (uninhibited control) [30].

• Velocity Measurements: Measure initial reaction velocities (Vâ‚€) for all combinations of substrate and inhibitor concentrations [30].

• Data Transformation: Calculate 1/Vâ‚€ for each measurement [30].

• Plot Generation: Create Dixon plot with [I] on x-axis and 1/Vâ‚€ on y-axis. Plot separate lines for each substrate concentration [30].

• Káµ¢ Determination: Identify the intersection point of the lines. The x-coordinate of this intersection provides -Káµ¢ [30].

• Inhibition Mechanism Identification: Competitive inhibition produces lines intersecting above the x-axis; non-competitive inhibition shows intersection on the x-axis; uncompetitive inhibition results in parallel lines [29].

Performance Assessment: Accuracy and Precision Analysis

Comparative Statistical Performance

A comprehensive simulation study comparing various estimation methods for Michaelis-Menten parameters revealed significant differences in accuracy and precision between linearization approaches [27]. The study employed Monte-Carlo simulation with 1,000 replicates of substrate concentration-time data, incorporating both additive and combined error models to assess methodological robustness [27].

Table 2: Performance Comparison of Enzyme Kinetic Parameter Estimation Methods

Estimation Method	Relative Accuracy	Relative Precision	Error Model Sensitivity	Remarks
Nonlinear Regression	Highest	Highest	Low	Gold standard; direct fitting without data transformation
Eadie-Hofstee	Moderate	Moderate	Moderate	Recommended linear method for parameter estimation
Lineweaver-Burk	Lowest	Lowest	High	Severe error distortion; educational use only
Dixon Plot	Variable	Variable	High	Specialized for inhibition studies; requires multiple [S]

The simulation results demonstrated that nonlinear regression methods provided the most accurate and precise parameter estimates, with superiority becoming more pronounced when data incorporated combined error models [27]. Among linearization methods, the Eadie-Hofstee approach generally outperformed the Lineweaver-Burk method due to its more balanced error distribution [27] [26].

Error Propagation and Methodological Limitations

All linear transformation methods distort experimental error structures, but to varying degrees [25] [26]. The Lineweaver-Burk plot is particularly problematic because it applies reciprocal transformation to both variables, dramatically amplifying errors at low substrate concentrations where measurements are typically least accurate [25]. For example, if V = 1±0.1, then 1/V = 1±0.1 (10% error), but if V = 10±0.1, then 1/V = 0.1±0.001 (1% error) [25]. This unequal error weighting biases parameter estimates and reduces reliability [25].

The Eadie-Hofstee plot partially mitigates this issue by avoiding reciprocal transformation of the measured velocity values, though it still incorporates V₀ in both coordinates, resulting in correlated errors [26]. All linearization methods assume that true initial velocities are measured, and deviations from this assumption – such as progressive enzyme inactivation during assay – can produce misleading linear plots with erroneous kinetic parameters [31].

The Researcher's Toolkit: Essential Reagents and Materials

Table 3: Essential Research Reagents for Enzyme Kinetic Studies

Reagent/Material	Specification	Functional Role	Quality Considerations
Purified Enzyme	High specific activity, known concentration	Biological catalyst	Stability, purity >95%, absence of contaminants
Substrate	High purity, solubility in buffer	Reactant molecule	Purity >99%, stability under assay conditions
Inhibitor Compounds	Known molecular weight, solubility	Inhibition studies	Purity >98%, stock solution stability
Buffer Components	Appropriate pKₐ, non-interfering	pH maintenance	Temperature consistency, ionic strength effects
Cofactors	As required by specific enzyme	Catalytic assistance	Stability, appropriate concentration
Detection Reagents	Spectrophotometric, fluorometric	Product quantification	Sensitivity, linear range, minimal background
Reference Standards	Authentic product compounds	Calibration	Certified purity, solution stability
4-Ethylresorcinol	4-Ethylresorcinol, CAS:2896-60-8, MF:C8H10O2, MW:138.16 g/mol	Chemical Reagent	Bench Chemicals
Rho-Kinase-IN-1	Rho-Kinase-IN-1, MF:C20H24N4S, MW:352.5 g/mol	Chemical Reagent	Bench Chemicals

Classical linearization methods have played a significant historical role in enzyme kinetics, providing accessible approaches for estimating kinetic parameters through graphical analysis. Among these methods, the Eadie-Hofstee plot generally offers superior performance for determining Kₘ and Vₘₐₓ due to its more balanced error weighting, while Dixon plots remain valuable for initial inhibition studies and Kᵢ estimation [26] [30].

However, contemporary research demands higher standards of accuracy and precision than these classical methods typically provide. Modern nonlinear regression techniques, implemented in software packages such as GraphPad Prism, MATLAB, and specialized tools like DynaFit and NONMEM, offer significantly improved parameter estimation by directly fitting the untransformed data to the Michaelis-Menten equation without distorting error structures [27] [25] [26]. These approaches have become the gold standard in rigorous enzyme kinetics research [27].

For researchers conducting inhibition studies, emerging methodologies like the 50-BOA (IC₅₀-Based Optimal Approach) demonstrate that precise estimation of inhibition constants is possible with dramatically reduced experimental requirements – potentially using just a single inhibitor concentration greater than the IC₅₀ value [32]. This represents a promising direction for increasing efficiency in enzyme inhibition analysis while maintaining accuracy.

While classical linearization methods retain value for educational purposes and initial data exploration, researchers engaged in drug development and precise biochemical characterization should prioritize nonlinear regression approaches for definitive parameter estimation, reserving linear transformations for preliminary analysis and visualization purposes.

In the field of enzyme kinetics, accurately determining inhibition constants (Ki) is crucial for understanding drug-drug interactions and chemical bioaccumulation. Researchers commonly employ various analytical methods to estimate these parameters from experimental data. This guide provides a comparative analysis of three predominant methods for analyzing enzyme inhibition data: Simultaneous Nonlinear Regression (SNLR), the KM,app method, and the Dixon linearization approach. Evaluation of quantitative performance data reveals that SNLR demonstrates superior robustness, accuracy, and efficiency, establishing it as the preferred methodology for reliable Ki determination in both pharmacological and environmental research contexts.

Enzyme inhibition occurs when a molecule (inhibitor) interferes with an enzyme's activity, reducing the rate of a metabolic reaction. This phenomenon is fundamental to drug action, toxicology, and cellular regulation. Competitive inhibition, a common mechanism, arises when an inhibitor competes with the substrate for binding to the enzyme's active site. The reaction scheme can be represented as a reversible equilibrium where the enzyme (E) binds either the substrate (S) to form a complex (ES) that yields product (P), or the inhibitor (I) to form an inactive complex (EI) [33].

The fundamental equation describing competitive inhibition is:

v = Vmax * [S] / [KM * (1 + [I]/Ki) + [S]]

Where:

• v is the initial reaction velocity
• Vmax is the maximum reaction velocity
• [S] is the substrate concentration
• KM is the Michaelis-Menten constant (substrate concentration at half Vmax)
• [I] is the inhibitor concentration
• Ki is the inhibition constant (dissociation constant for the enzyme-inhibitor complex)

The Ki value quantitatively represents the inhibitor's potency; a lower Ki indicates stronger binding and more effective inhibition. Accurate determination of Ki is therefore critical for predicting metabolic interactions, such as those occurring when multiple drugs are administered concurrently [33] [34].

Methodologies for Determining Inhibition Constants

Simultaneous Nonlinear Regression (SNLR)

Experimental Protocol: SNLR requires initial velocity measurements at multiple substrate concentrations across a range of inhibitor concentrations, including a control with no inhibitor. The entire dataset is fitted simultaneously to the competitive inhibition equation using nonlinear regression algorithms. This method directly estimates all parameters (Vmax, KM, and Ki) by minimizing the sum of squared residuals between observed and predicted reaction velocities [35].

KM,app Method

Experimental Protocol: This two-step approach first involves separately fitting the Michaelis-Menten equation to velocity data at each inhibitor concentration, obtaining an apparent KM (KM,app) for each. In the second step, these KM,app values are plotted against the corresponding inhibitor concentrations. The Ki is then determined from the x-intercept of this linear plot, where KM,app = -Ki [35].

Dixon Plot (Linearization)

Experimental Protocol: The Dixon method uses a linear transformation of the Michaelis-Menten equation. Researchers measure reaction rates at one or two substrate concentrations across varying inhibitor levels. They then plot the reciprocal of velocity (1/v) against inhibitor concentration ([I]). For competitive inhibition, these lines intersect at a point where [I] = -Ki, providing an estimate of the inhibition constant [35].

Comparative Performance Analysis

A comprehensive simulation study directly compared the performance of these three methods for estimating Ki values across a wide range of KM/Ki ratios (from <0.1 to >600). The results demonstrate clear differences in method performance [35].

Table 1: Quantitative Comparison of Ki Estimation Methods

Method	Parameter Recovery	Computational Efficiency	Implementation Complexity	Robustness to Error
SNLR	Excellent (Accurate KM, VMAX, and Ki)	Highest	Fastest and easiest	Most robust
KM,app Method	Good Ki estimates	Moderate	More time-consuming	Moderately robust
Dixon Plot	Inaccurate and widely ranging Ki	N/A	Simple but unreliable	Least robust

The superiority of SNLR is particularly evident in its handling of experimental error. When metabolic formation rates were simulated with random error (10% coefficient of variation), SNLR provided significantly more accurate and precise Ki estimates compared to the other methods. The Dixon method, despite its historical popularity and simplicity, produced "widely ranging and inaccurate estimates of Ki" according to the controlled simulations [35].

Experimental Protocols for Robust Enzyme Inhibition Studies

Sample Preparation and Characterization

Liver S9 Fraction Protocol:

• Tissue Homogenization: Clear liver tissue of blood and homogenize in 2-4 volumes of ice-cold buffer (e.g., 150 mM KCl, 50 mM Tris, 1 mM dithiothreitol, 2 mM EDTA, 250 mM sucrose, pH 7.8) using a Potter-Elvehjem mortar and pestle with 4-5 strokes.
• Centrifugation: Centrifuge the homogenate at 13,000 × g for 20 minutes at 4°C.
• Aliquoting and Storage: Collect the supernatant (S9 fraction), aliquot into small volumes (e.g., 0.5 mL), flash-freeze in liquid nitrogen, and store at -80°C until use [33].

Enzyme Activity Characterization:

• CYP450 Activity: Measure via ethoxyresorufin O-dealkylation (EROD) assay.
• GST Activity: Assess by monitoring glutathione conjugation of 1-chloro-2,4-dinitrobenzene (CDNB).
• UGT Activity: Determine using p-nitrophenol (p-NP) glucuronidation assays.
• Perform all assays in quadruplicate at physiologically relevant temperature and pH [33].

Data Collection for SNLR Analysis

Substrate Depletion Approach:

• Incubation Conditions: Use environmentally/pharmacologically relevant substrate and inhibitor concentrations. For PAH studies, examples include phenanthrene, pyrene, and benzo[a]pyrene as binary mixtures.
• Time Course Measurements: Monitor substrate depletion over time to determine initial rates.
• Replicate Design: Include adequate replication (minimum n=3-4) for statistical power.
• Control Experiments: Always include control incubations without inhibitor and without enzyme to account for non-enzymatic degradation [33].

Optimal Experimental Design: Recent research suggests that informative data for precise Ki estimation can be obtained using a single inhibitor concentration greater than the IC50 value, substantially reducing experimental requirements while maintaining accuracy. This model-informed approach allows for a more than 75% reduction in required data points while achieving equal or improved precision compared to conventional designs [34].

SNLR Data Analysis Workflow

The Scientist's Toolkit: Essential Research Reagents

Table 2: Key Research Reagents for Enzyme Inhibition Studies

Reagent/Chemical	Function/Application	Example Use in Inhibition Studies
Liver S9 Fractions	Source of metabolic enzymes	Provide complete phase I and II enzyme systems for substrate depletion studies [33]
β-NADPH	Cofactor for CYP450 enzymes	Essential for cytochrome P450-mediated reactions; required in incubation mixtures [33]
Substrate Compounds	Molecules whose metabolism is studied	PAHs (phenanthrene, pyrene, benzo[a]pyrene) or specific drug substrates [33]
Inhibitor Compounds	Molecules that reduce enzyme activity	Test compounds for inhibition potential; included at varying concentrations [33]
UDPGA	Cofactor for UGT enzymes	Required for glucuronidation reactions in phase II metabolism [33]
Reduced Glutathione (GSH)	Cofactor for GST enzymes	Essential for glutathione conjugation reactions [33]
Alamethicin	Pore-forming peptide	Activates UDP-glucuronosyltransferase activity in membrane preparations [33]
Model Substrates	Probe compounds for specific enzymes	7-ethoxyresorufin (CYP1A), CDNB (GST), p-nitrophenol (UGT) [33]
Papain Inhibitor	Papain Inhibitor, MF:C19H29N7O6, MW:451.5 g/mol	Chemical Reagent
pnu-176798	pnu-176798, MF:C16H13FN4O3S, MW:360.4 g/mol	Chemical Reagent

Methodological Comparison Visualization

The comparative analysis of methods for determining enzyme inhibition constants demonstrates the clear superiority of Simultaneous Nonlinear Regression (SNLR). This approach outperforms both the KM,app method and traditional Dixon linearization in accuracy, precision, and efficiency. SNLR's robustness to experimental error and its ability to provide reliable parameter estimates with realistic confidence intervals make it particularly valuable for modern pharmacological research and environmental risk assessment.

For researchers designing enzyme inhibition studies, implementing SNLR with optimal experimental designs—potentially incorporating model-informed approaches that reduce data requirements—represents the current gold standard for generating reliable, reproducible Ki values that accurately reflect inhibitor potency and inform critical decisions in drug development and chemical safety assessment.

Enzyme inhibition analysis is a cornerstone of drug development, essential for predicting drug-drug interactions and evaluating inhibitor potency as recommended by the U.S. Food and Drug Administration [32] [3]. Traditionally, estimating inhibition constants (Kic and Kiu) has required extensive experimental data involving multiple substrate and inhibitor concentrations—an approach utilized in over 68,000 studies since its introduction in 1930 [32]. However, inconsistencies across studies highlight the need for more systematic experimental designs, particularly when prior knowledge of inhibition type is unavailable [3].

This comparison guide examines a groundbreaking methodological framework—the IC50-Based Optimal Approach (50-BOA)—that challenges conventional paradigms by enabling precise estimation of inhibition constants using a single inhibitor concentration. We objectively evaluate its performance against traditional methods, supported by experimental data and implementation protocols.

Understanding Enzyme Inhibition Constants

Fundamental Concepts and Significance

Enzyme inhibition occurs when a substance (inhibitor) reversibly binds to an enzyme (competitive), enzyme-substrate complex (uncompetitive), or both (mixed) [3]. The key parameters characterizing these interactions are the inhibition constants:

• Kic: Dissociation constant between inhibitor and free enzyme
• Kiu: Dissociation constant between inhibitor and enzyme-substrate complex

These constants represent both inhibitor potency and mechanism, with lower values indicating higher binding affinity [32] [3]. Their accurate estimation is crucial for predicting in vivo enzyme inhibition through mathematical models derived from in vitro experiments [32].

The Traditional Approach to Estimation

The canonical method for estimating inhibition constants follows a well-established protocol [32] [3]:

• IC50 Determination: Estimate half-maximal inhibitory concentration using various inhibitor concentrations with a single substrate concentration (typically KM)
• Experimental Design: Establish conditions with ST at 0.2KM, KM, and 5KM and IT at 0, 1/3 IC50, IC50, and 3IC50
• Velocity Measurement: Measure initial reaction velocity for each concentration combination
• Model Fitting: Fit the mixed inhibition model to the data to estimate constants

This approach generates 12 data points and relies on the general equation for mixed inhibition [32]:

The 50-BOA Method: A Paradigm Shift

Theoretical Foundation and Innovation

The 50-BOA method emerged from analyzing error landscapes of estimations across various experimental designs [32] [3]. Researchers discovered that nearly half of conventional data is dispensable and potentially bias-inducing [3]. The key insight was that precise estimation becomes possible when using a single inhibitor concentration greater than IC50 while incorporating the harmonic mean relationship between IC50 and inhibition constants into the fitting process [32].

The method specifically addresses the challenge of estimating two inhibition constants for mixed inhibition without prior knowledge of inhibition type—a significant limitation of previous single-concentration methods [32] [3].

Experimental Design and Workflow

The 50-BOA workflow represents a substantial simplification compared to traditional approaches:

Computational Implementation

The researchers provide user-friendly MATLAB and R packages that automate the estimation process [36]. The core implementation involves:

• Data Formatting: Organizing initial velocity data in a defined Excel format with Vmax, KM, IC50, and experimental setups
• Condition Checking: The 'BOA_Condition' function verifies data sufficiency (presence of IT ≥ IC50 and distinct ST values within 0.2KM to 5KM)
• Cross-Validation: The 'CV_Inhibition' function selects appropriate regularization constants
• Error Landscape Analysis: The main function estimates inhibition constants with confidence intervals and generates diagnostic heatmaps [36]

The package also extends to specialized systems including bi-substrate mechanisms, substrate cooperativity, and inhibitor cooperativity [36].

Comparative Performance Analysis

Experimental Requirements and Efficiency

The 50-BOA method demonstrates remarkable efficiency improvements over traditional approaches:

Table 1: Method Efficiency Comparison

Parameter	Traditional Method	50-BOA Method	Improvement
Number of inhibitor concentrations required	4	1	75% reduction
Minimum total data points	12	3	75% reduction
Prior knowledge of inhibition type	Required	Not required	More versatile
Experimental time and resources	High	Minimal	Substantial savings
Applicability to mixed inhibition	Limited	Excellent	Broader application

Precision and Accuracy in Experimental Applications

The method has been validated through multiple experimental applications:

Table 2: Experimental Validation Data

Enzyme-Inhibitor Pair	Method	Kic (μM)	Kiu (μM)	Confidence Interval	Reference
Triazolam-Ketoconazole (CYP3A4)	Traditional	Varied reported values	Inconsistent across studies	[32]
Triazolam-Ketoconazole (CYP3A4)	50-BOA	Precise estimation	Narrow CI	[3]
Chlorzoxazone-Ethambutol	Traditional	0.0367	0.0766	Extremely wide (0.0244-1.59×10^12)	[36]
Chlorzoxazone-Ethambutol	50-BOA	0.0398	0.0403	Narrow (0.0358-0.0460, 0.0337-0.0482)	[36]

The 50-BOA method consistently produces narrower confidence intervals, indicating superior precision. In test cases, the traditional method generated implausibly wide confidence intervals (e.g., 0.0244-1.59×10^12 for Kic), while 50-BOA provided biologically meaningful ranges [36].

Error Landscape Analysis

The theoretical foundation of 50-BOA involves analyzing error landscapes to identify optimal experimental designs [32] [3]. Key findings include:

• Low IT Limitations: When IT is much lower than Kic and Kiu, the error landscape shows broadly distributed dark regions, indicating poor identifiability of inhibition constants
• Optimal Conditions: Precise estimation requires IT > IC50, which creates well-defined minima in the error landscape
• Regularization Benefits: Incorporating the IC50-inhibition constant relationship acts as effective regularization, constraining the parameter space and improving identifiability [32]

Practical Implementation Guide

Research Reagent Solutions

Table 3: Essential Research Materials for 50-BOA Implementation

Reagent/Resource	Function/Role	Specification Notes
50-BOA Software Package	Computational implementation of the method	Available for MATLAB and R; includes auxiliary functions for condition checking and cross-validation [36]
Enzyme Inhibition Data	Experimental input for analysis	Formatted Excel files with Vmax, KM, IC50, and initial velocity measurements [36]
IC50 Estimation Assay	Preliminary inhibitor potency assessment	Standard enzyme activity measurements with varying inhibitor concentrations [32]
Multi-substrate Velocity Assay	Core experimental data generation	Initial velocity measurements with single IT > IC50 and varying ST values [3]

Step-by-Step Experimental Protocol

• Preliminary IC50 Determination

  • Perform standard enzyme activity assays with a range of inhibitor concentrations (0-3×IC50)
  • Use a single substrate concentration (typically KM)
  • Fit dose-response curve to calculate IC50 value

• Experimental Design for 50-BOA

  • Select a single inhibitor concentration > IC50
  • Choose at least two different substrate concentrations within 0.2KM to 5KM
  • Measure initial reaction velocities for these conditions

• Computational Analysis

  • Format data according to package requirements
  • Run Error_Landscape function with appropriate parameters
  • Verify data adequacy using BOA_Condition output
  • Extract inhibition constants with confidence intervals

• Validation and Interpretation

  • Check confidence interval width for precision assessment
  • Compare Kic and Kiu values to determine inhibition type
  • Utilize error landscape visualization for diagnostic purposes

The 50-BOA method represents a significant advancement in enzyme inhibition analysis, addressing critical limitations of traditional approaches while maintaining—and often enhancing—estimation precision. By reducing experimental requirements by over 75% and eliminating the need for prior knowledge of inhibition type, this approach offers substantial practical benefits for drug development pipelines and biochemical research.

The incorporation of error landscape analysis and IC50-based regularization provides a robust theoretical foundation, while user-friendly computational packages ensure accessibility for researchers across disciplines. As the field continues to prioritize efficiency and reproducibility, methodologies like 50-BOA establish new standards for biochemical characterization in pharmaceutical and academic settings.

The quantitative assessment of enzyme inhibition is a cornerstone of modern drug discovery. The inhibition constant (Ki), a direct measure of an inhibitor's binding affinity for its target enzyme, serves as a crucial parameter for ranking compound potency, defining selectivity, and predicting in vivo efficacy. This guide provides a comparative analysis of experimental approaches for determining inhibition constants, framed through case studies from three therapeutically significant enzyme families: monoamine oxidases (MAOs), cholinesterases, and HIV-1 protease. The accurate determination of these constants is not merely an academic exercise; it directly impacts the reliability of drug candidate selection and the understanding of therapeutic mechanisms. However, as we will explore, the experimental conditions under which Ki values are determined can profoundly influence the results, necessitating rigorous and well-optimized protocols [37].

Monoamine Oxidase Inhibitors: From Natural Products to Selective Therapeutics

Background and Therapeutic Significance

Monoamine oxidases (MAO-A and MAO-B) are flavin-dependent enzymes bound to the outer mitochondrial membrane. They catalyze the oxidative deamination of neurotransmitters such as serotonin, dopamine, and norepinephrine. Although they share 70% sequence identity, they exhibit distinct substrate and inhibitor specificities. Selective MAO-A inhibitors are effective in the treatment of depression, while MAO-B inhibitors are useful for Parkinson's disease, Alzheimer's disease, and also depression [38]. This therapeutic importance makes the accurate characterization of MAO inhibitors a vital activity in neuropharmacology.

Case Study: Kinetics of MAO Inhibition by Propolis Flavonoids

Dichloromethane extracts of propolis show potent, dose-dependent inhibition of both human MAO-A and MAO-B. Bioassay-guided fractionation identified the flavonoids galangin and apigenin as the principal inhibitory constituents. The kinetics of inhibition were characterized using recombinant human MAO enzymes, revealing that the binding of both flavonoids is reversible and time-independent [38].

The experimental protocol typically involves:

• Enzyme Source: Recombinant human MAO-A and MAO-B.
• Assay Conditions: A standard reaction mixture containing the enzyme, a buffer (e.g., phosphate buffer, pH 7.4), and a fluorogenic or chromogenic substrate (e.g., kynuramine for MAO-A, benzylamine for MAO-B).
• Inhibition Measurement: The test compound (e.g., galangin or apigenin) is incubated with the enzyme, and the reaction is initiated by adding the substrate. The initial velocity of the reaction is measured, often by detecting a fluorescent or colored product.
• Data Analysis: The mechanism of inhibition is determined by analyzing the initial velocity data at varying substrate and inhibitor concentrations. For galangin and apigenin, Lineweaver-Burk plots indicated a competitive mechanism, meaning the inhibitors bind directly to the enzyme's active site, competing with the substrate. The inhibition constant (Ki) is then calculated from this data [38].

Table 1: Inhibition of Recombinant Human MAO-A and MAO-B by Propolis Extract and its Constituents

Sample Name	Monoamine Oxidase-A (ICâ‚…â‚€)	Monoamine Oxidase-B (ICâ‚…â‚€)	Selectivity (A/B)
Propolis Extract	0.60 ± 0.12 μg/mL	6.99 ± 0.09 μg/mL	~10-fold (A)
Galangin	0.13 ± 0.01 μM	3.65 ± 0.15 μM	~28-fold (A)
Apigenin	0.64 ± 0.11 μM	1.12 ± 0.27 μM	~1.7-fold (A)
Quercetin	2.44 ± 0.12 μM	38.66 ± 1.20 μM	~16-fold (A)
Clorgyline (Ref.)	0.0065 ± 0.0003 μM	-	-
Deprenyl (Ref.)	-	0.036 ± 0.0012 μM	-

Data adapted from [38]. IC₅₀ values are Mean ± S.D. Ref.: Reference inhibitor.

Cholinesterase Inhibitors: Stopped-Flow Kinetics and Pesticide Detection

Background and Significance

Cholinesterases (ChEs), including acetylcholinesterase (AChE), are key enzymes in the nervous system, responsible for hydrolyzing the neurotransmitter acetylcholine. Inhibitors of cholinesterases have applications ranging from the treatment of neurodegenerative diseases like Alzheimer's (e.g., donepezil) to use as pesticides (carbamates and organophosphates). The analysis of ChE inhibition is therefore critical in both neuroscience and environmental safety.

Case Study: Stopped-Flow Instrumentation for Kinetic Analysis

Stopped-flow instrumentation is a rapid-kinetics technique used to study fast enzymatic reactions, including the inhibition of cholinesterases. This method allows for the efficient and simultaneous determination of inhibitory potency for compounds like carbaryl and phoxim [39].

A generalized experimental protocol involves:

• Instrumentation: A stopped-flow apparatus, which rapidly mixes small volumes of enzyme and substrate/inhibitor solutions and monitors the reaction in real-time.
• Reaction Monitoring: The enzymatic reaction is typically followed by a change in absorbance or fluorescence. For AChE, a common assay uses acetylthiocholine as a substrate, which is hydrolyzed to thiocholine. Thiocholine then reacts with DTNB (Ellman's reagent) to produce a yellow-colored product that can be measured spectrophotometrically.
• Data Collection: The instrument records the initial velocity of the reaction over a very short time (milliseconds), which is essential for accurately determining kinetics before significant substrate depletion or product accumulation occurs.
• Kinetic Analysis: The initial velocity data, collected at different inhibitor concentrations, is fitted to an appropriate inhibition model (e.g., competitive, non-competitive) to determine the Ki value. This approach is particularly useful for characterizing the rapid, reversible inhibition caused by many carbamate pesticides [39].

HIV-1 Protease Inhibitors: Combating Resistance with Ultra-Potent Inhibitors

Background and Therapeutic Challenge

HIV-1 protease (PR) is an aspartic protease that is essential for viral maturation, making it a prime target for antiretroviral therapy. The emergence of drug-resistant HIV strains has driven the development of increasingly potent inhibitors, such as darunavir (DRV). Characterizing these high-affinity inhibitors, which have Ki values in the picomolar range, presents unique experimental challenges, as traditional enzyme kinetics assays are often insufficient [40] [41].

Case Study 1: Mixed-Type Inhibition of HIV-1 Protease by Darunavir

Kinetic analysis of darunavir revealed an unusual mixed-type competitive-uncompetitive inhibition mechanism for both wild-type HIV-1 PR and the V32I mutant. This is consistent with structural data showing that, in addition to the primary binding site in the active-site cavity, DRV can bind to a second, allosteric site on the protease dimer surface [40].

The experimental protocol for this finding included:

• Enzyme Preparation: Wild-type and mutant (V32I) HIV-1 protease.
• Fluorescence Assay: Using a specific anthranylyl/p-NO2-Phe containing substrate that mimics a natural viral cleavage site. The increase in fluorescence upon substrate cleavage is measured.
• Kinetic Measurements: Initial velocities are measured at a range of substrate and inhibitor concentrations.
• Data Fitting: The data for DRV and the chemically related amprenavir (APV) fitted a parabolic mixed-type mechanism. The velocity equation accounted for inhibitor binding at two non-mutually exclusive sites, forming a ternary complex (PR-DRVâ‚‚). In contrast, saquinavir (SQV), which lacks the structural motifs for the second site, displayed purely competitive inhibition [40].

Table 2: Kinetic Parameters for Inhibition of HIV-1 Protease (PRWT and PRV32I)

Inhibitor	PR Form	Ki (Competitive) nM	Ki (Uncompetitive) nM	Inhibition Mechanism
Darunavir (DRV)	PRWT	22	18	Mixed (Competitive-Uncompetitive)
Darunavir (DRV)	PRV32I	24	16	Mixed (Competitive-Uncompetitive)
Amprenavir (APV)	PRWT	4.5	20	Mixed (Competitive-Uncompetitive)
Saquinavir (SQV)	PRWT	0.4	-	Competitive

Data summarized from [40]. The mixed mechanism for DRV and APV suggests binding at two sites.

Case Study 2: A Hypersensitive Fluorogenic Assay for Picomolar Ki Determination

To accurately measure the sub-nanomolar Ki values of next-generation HIV-1 PR inhibitors like darunavir, a hypersensitive assay was developed using a novel fluorogenic substrate. This substrate (sequence: Arg-Arg-EDANS-GSGIFLETSL-Lys(sDABCYL)-Arg) exhibits an exceptional 104-fold increase in fluorescence upon cleavage and excellent kinetic parameters (kcat of 7.4 s⁻¹, KM of 15 μM) [41].

The key steps in this advanced protocol are:

• Substrate Design: The substrate incorporates the EDANS/DABCYL FRET pair, optimized for high sensitivity at the low pH optimal for HIV-1 PR activity.
• Ultra-Low Enzyme Concentration: The assay's sensitivity allows the enzyme concentration to be reduced to 25 pM, which is close to the Kd value of the protease dimer. This is critical for accurately characterizing tight-binding inhibitors.
• Inhibition Assay: Initial velocities are measured at a fixed, low enzyme concentration and varying inhibitor concentrations.
• Data Analysis with Morrison's Equation: Because the Ki values are far below the enzyme concentrations used in traditional assays, the data are fitted using Morrison's equation for tight-binding inhibitors. This method allowed for the determination of a Ki value of 10 pM for darunavir, 135 pM for amprenavir, and 82 pM for tipranavir. The authors note this assay is capable of measuring Ki values as low as 0.25 pM [41].

Comparative Analysis of Methodologies and Experimental Considerations

Optimizing Experimental Design: The 50-BOA Approach

A significant challenge in enzyme kinetics is the traditional requirement for extensive data collection across multiple substrate and inhibitor concentrations. A recent systematic analysis of error landscapes in estimation procedures revealed that nearly half of conventional data points are dispensable and can even introduce bias. The proposed solution, the ICâ‚…â‚€-Based Optimal Approach (50-BOA), incorporates the relationship between the half-maximal inhibitory concentration (ICâ‚…â‚€) and the inhibition constants into the fitting process. This allows for precise and accurate estimation of Ki values using data from a single inhibitor concentration that is greater than the ICâ‚…â‚€, reducing the number of required experiments by over 75% without sacrificing reliability [3]. This approach is applicable across inhibition types (competitive, uncompetitive, mixed), making it highly versatile for drug discovery workflows.

Critical Considerations for Ki Determination

The quantitative data derived from these studies are powerful, but their interpretation requires caution. The experimentally determined Ki is widely used to rank inhibitor affinity; however, it is not an absolute physical constant independent of assay conditions. For instance, adsorption of the bis(7)-tacrine inhibitor to the surface of glass containers dramatically increased its observed Ki against acetylcholinesterase from 2.9 pM (in plastic containers) to 3.2 nM. Furthermore, binding of the inhibitor to inactive enzyme also significantly altered the measured Ki. These findings caution against using Ki values to rank-order binding potencies or benchmark computational methods without a detailed understanding of the assay conditions used [37].

The Scientist's Toolkit: Key Research Reagent Solutions

Table 3: Essential Research Reagents for Enzyme Inhibition Studies

Reagent / Resource	Function and Application	Example/Case Study
Recombinant Human MAOs	Provides a consistent and pure enzyme source for high-throughput screening and kinetic studies of MAO inhibitors.	Inhibition kinetics of galangin and apigenin [38].
FRET-Based Substrates	Enable continuous, highly sensitive fluorescence-based activity assays. The signal is generated upon cleavage by the target enzyme.	Hypersensitive HIV-1 protease substrate (EDANS/DABCYL) [41].
Stopped-Flow Instrumentation	Allows for the rapid mixing of reagents and measurement of initial reaction velocities on a millisecond timescale for fast enzymatic reactions.	Kinetic analysis of cholinesterase inhibition by pesticides [39].
Tight-Binding Analysis Software	Implements algorithms (e.g., Morrison's equation) to fit kinetic data and accurately determine Ki values for inhibitors with very high affinity, where [I] ≈ [E].	Determination of picomolar Ki values for HIV-1 protease inhibitors [41].
ICâ‚…â‚€-Based Optimal Approach (50-BOA)	A computational package (available for MATLAB and R) that optimizes experimental design, enabling precise Ki estimation from a single, well-chosen inhibitor concentration.	Efficient estimation of inhibition constants for all inhibition types, reducing experimental burden [3].
Chymase-IN-1	Chymase-IN-1, MF:C20H15ClNO4PS, MW:431.8 g/mol	Chemical Reagent
Nhe3-IN-1	Nhe3-IN-1, MF:C12H10ClN3S, MW:263.75 g/mol	Chemical Reagent

The case studies presented here illustrate a clear continuum in the development of enzyme inhibition analysis. From the characterization of natural product inhibitors like galangin for MAO to the engineering of ultra-potent, multi-targeting drugs like darunavir for HIV-1, the accurate determination of inhibition constants remains paramount. The field is moving toward more efficient, precise, and sensitive methods, as evidenced by the development of hypersensitive assays and optimized experimental designs like the 50-BOA. For researchers, the key takeaway is that the choice of assay protocol, the quality of reagents, and a critical understanding of the underlying kinetics are not mere technical details—they are fundamental to generating reliable data that can drive successful drug discovery campaigns from the bench to the clinic.

Visual Workflows

HIV-1 Protease Mixed Inhibition Mechanism

50-BOA Optimal Experimental Workflow

Troubleshooting Experimental Pitfalls and Optimizing Assay Design for Reliable Ki Determination

The accurate determination of enzyme inhibition constants (Káµ¢) represents a cornerstone of drug development and biochemical research, providing critical insights into inhibitor potency and mechanism of action [3]. For decades, scientists have relied on linear transformation methods, such as Lineweaver-Burk plots, to estimate these parameters from experimental data. These approaches transform the hyperbolic Michaelis-Menten equation into a linear form, allowing graphical determination of Káµ¢ values [42]. While mathematically convenient, these linearization techniques introduce significant statistical biases and analytical limitations that can compromise the reliability of inhibition constant estimates [42].

The conventional enzyme inhibition analysis workflow typically involves measuring initial reaction velocities across multiple substrate and inhibitor concentrations, often requiring 12 or more experimental conditions to characterize a single inhibitor [3]. Researchers traditionally use a canonical approach with substrate concentrations at 0.2Kₘ, Kₘ, and 5Kₘ alongside inhibitor concentrations at 0, ¹/₃IC₅₀, IC₅₀, and 3IC₅₀ [3]. This resource-intensive process has been employed in more than 68,000 studies since its introduction in 1930, despite unresolved questions about its optimality and sufficiency for precise estimation [3] [34].

Within this context, this analysis provides a comparative evaluation of traditional linear transformation methods alongside emerging innovative approaches, with particular focus on experimental protocols, data requirements, and statistical robustness. By objectively examining the limitations of conventional practices and validating alternative methodologies with experimental data, this guide aims to support researchers in selecting optimal strategies for enzyme inhibition constant determination.

Limitations of Linear Transformation Methods

Statistical and Practical Drawbacks

Linear transformation methods, particularly the Lineweaver-Burk (double-reciprocal) plot, introduce significant statistical artifacts that compromise data interpretation. The mathematical process of reciprocaling reaction rate (1/v) and substrate concentration (1/[S]) disproportionately amplifies errors at low substrate concentrations, where measurement precision is typically lowest [42]. This error distortion creates systematic biases in parameter estimation, often leading researchers to underestimate Vmax by 10-20% when using hyperbolic plots [42]. Since Kₘ estimates derive from Vmax determination, this inaccuracy propagates through the entire kinetic analysis.

The limitations extend beyond statistical considerations to practical experimental challenges. Traditional inhibition analysis requires extensive data collection across multiple substrate and inhibitor concentrations, typically utilizing 12 distinct experimental conditions [3]. This resource-intensive approach demands substantial quantities of enzymes and inhibitors, particularly problematic when working with scarce or expensive compounds. Furthermore, the conventional method assumes prior knowledge of inhibition type for optimal experimental design, creating a circular dependency where researchers must understand the mechanism before they can properly characterize it [3].

Identification Challenges in Inhibition Typing

Linear plots provide characteristic patterns for different inhibition mechanisms, but these patterns become ambiguous with experimental error. Competitive inhibition displays lines converging on the y-axis, non-competitive inhibition shows lines converging on the x-axis, and uncompetitive inhibition produces parallel lines [42] [43]. In practice, however, mixed inhibition often occurs, presenting patterns that are kinetically indistinguishable from pure non-competitive inhibition in Lineweaver-Burk plots [42]. This ambiguity frequently leads to misclassification of inhibition mechanisms, as demonstrated by the conflicting reports for cytochrome P450 CYP3A4 inhibition by ketoconazole, variably classified as both mixed and competitive in different studies [3].

The problem is particularly pronounced for uncompetitive inhibition, which remains rare and difficult to distinguish experimentally [44]. Traditional decision systems often fail to identify uncompetitive inhibitors, with one study reporting 0% recovery using conventional methods compared to 38% using an improved system that quantifies the ratio between inhibition constants [45]. These classification errors have direct practical consequences, as clinical management strategies differ significantly based on inhibition type—dose adjustments effectively mitigate risks for competitive inhibitors but prove less effective for uncompetitive inhibition [3].

Table 1: Characteristic Patterns and Limitations in Linear Transformation Analysis

Inhibition Type	Lineweaver-Burk Pattern	Vmax Effect	Kₘ Effect	Common Identification Errors
Competitive	Lines converge on y-axis	Unchanged	Increases	Misclassification as mixed type
Non-competitive	Lines converge on x-axis	Decreases	Unchanged	Rare; often confused with mixed
Uncompetitive	Parallel lines	Decreases	Decreases	Frequent failure to identify
Mixed	Lines converge between axes	Decreases	Increases/Decreases	Misclassified as pure non-competitive

Innovative Approaches to Inhibition Constant Estimation

The 50-BOA Framework

A novel methodology termed the ICâ‚…â‚€-Based Optimal Approach (50-BOA) addresses fundamental limitations of traditional analysis by incorporating the harmonic mean relationship between ICâ‚…â‚€ and inhibition constants into the fitting process [3] [34]. This approach enables precise estimation of inhibition constants using data from a single inhibitor concentration greater than ICâ‚…â‚€, substantially reducing experimental requirements while improving accuracy [34]. The mathematical foundation of 50-BOA integrates the known weighted harmonic mean relationship:

[ \frac{1}{IC{50}} = \frac{\alpha}{K{ic}} + \frac{1-\alpha}{K{iu}} = \frac{1}{H(K{ic},K{iu})}, \quad \alpha = \frac{KM}{ST + KM} ]

This relationship ensures that selecting Iₜ ≥ IC₅₀ guarantees Iₜ ≥ Kᵢc or Iₜ ≥ Kᵢu, providing a practical criterion for collecting informative data while avoiding bias [34]. The 50-BOA incorporates this relationship as an IC₅₀-based regularization term in the error minimization function:

[ \text{Total error} = \text{fitting error} + \lambda \times \left( \frac{IC{50} - H(K{ic}, K{iu})}{IC{50}} \right)^2 ]

where λ is a regularization constant determined through cross-validation [34]. This approach achieves accuracy comparable to conventional methods while reducing required experimental data by more than 75% [3].

Diagram 1: 50-BOA Experimental Workflow - This optimized approach reduces experimental requirements by >75% compared to conventional methods.

Error Landscape Analysis for Experimental Design

The theoretical foundation for 50-BOA emerged from comprehensive error landscape analysis across various experimental conditions [3] [34]. This investigation revealed that estimation precision varies dramatically depending on the relationship between inhibitor concentration (Iₜ) and the inhibition constants Kᵢc and Kᵢu. When Iₜ is substantially lower than both inhibition constants (Iₜ << Kᵢc and Iₜ << Kᵢu), the error landscape shows a broadly distributed dark region across possible Kᵢc and Kᵢu values, indicating poor identifiability and imprecise estimation [3]. This explains why conventional multi-concentration approaches that include low inhibitor concentrations often yield inconsistent results across studies.

The analysis demonstrated that nearly half of conventional experimental data is dispensable and potentially introduces bias rather than improving estimation [3]. By focusing experimental efforts on informative data points where Iₜ exceeds at least one inhibition constant, researchers can achieve superior precision with dramatically reduced experimental burden. This principled approach to experimental design represents a significant advancement over traditional empirically-established conditions whose optimality remained unproven.

Table 2: Quantitative Comparison of Inhibition Analysis Methods

Methodological Aspect	Traditional Multi-Concentration Approach	50-BOA Framework	Improvement/Change
Required inhibitor concentrations	4 (0, ¹/₃IC₅₀, IC₅₀, 3IC₅₀)	1 ([I] ≥ IC₅₀)	75% reduction
Required substrate concentrations	3 (0.2Kₘ, Kₘ, 5Kₘ)	3 (0.2Kₘ, Kₘ, 5Kₘ)	No change
Total experimental conditions	12	3	75% reduction
Prior knowledge requirement	Inhibition type preferred	None required	Expanded applicability
Precision with mixed inhibitors	Highly variable between studies	Consistently high	Substantial improvement
Handling of low-affinity inhibitors	Problematic due to low [I] data	Robust via ICâ‚…â‚€ relationship	Major enhancement

Experimental Protocols and Validation

Protocol: Traditional Multi-Concentration Method

The canonical enzyme inhibition constant estimation protocol begins with determination of IC₅₀ values from percentage control activity data across various inhibitor concentrations at a single substrate concentration, typically equal to Kₘ [3]. Subsequently, researchers establish an experimental design using substrate concentrations at 0.2Kₘ, Kₘ, and 5Kₘ combined with inhibitor concentrations at 0, ¹/₃IC₅₀, IC₅₀, and 3IC₅₀ [3]. For each combination, measure initial velocity (V₀) by determining the slope of product formation progress curves at time zero or measuring reaction extent over very brief time intervals where linearity is maintained [42].

The mixed inhibition model is then fitted to the collected data:

[ V0 = \frac{V{\max} ST}{KM \left( 1 + \frac{IT}{K{ic}} \right) + ST \left( 1 + \frac{IT}{K_{iu}} \right)} ]

where Sₜ, Iₜ, and Eₜ denote total substrate, inhibitor, and enzyme concentrations, respectively; Vmax represents maximal velocity; and Kₘ is the Michaelis-Menten constant [3]. Inhibition constants Kᵢc and Kᵢu are estimated through nonlinear regression analysis of the dataset. Finally, inhibition type is identified based on the relative magnitudes of the estimated constants: competitive if Kᵢc << Kᵢu, uncompetitive if Kᵢu << Kᵢc, and mixed if the constants have comparable magnitudes [3].

Protocol: 50-BOA Implementation

The 50-BOA protocol modifies the traditional approach by leveraging the harmonic mean relationship between IC₅₀ and inhibition constants. Begin similarly with IC₅₀ determination from percentage control activity data at a substrate concentration equal to Kₘ [3]. Rather than implementing multiple inhibitor concentrations, design experiments using a single inhibitor concentration greater than the estimated IC₅₀ value, combined with multiple substrate concentrations (typically 0.2Kₘ, Kₘ, and 5Kₘ) [34]. Measure initial velocities (V₀) for each substrate concentration at this single inhibitor concentration using the same progress curve methodology as the traditional approach.

The key differentiator comes in the fitting process: implement a modified error function that incorporates ICâ‚…â‚€ as a regularization term:

[ \text{Total error} = \sum \left( \frac{V{0,\text{obs}} - V{0,\text{pred}}}{V{0,\text{obs}}} \right)^2 + \lambda \times \left( \frac{IC{50} - H(K{ic}, K{iu})}{IC_{50}} \right)^2 ]

where H(Kᵢc, Kᵢu) represents the harmonic mean of the inhibition constants, and λ is determined through cross-validation [34]. Estimate inhibition constants Kᵢc and Kᵢu by minimizing this total error function. Finally, identify inhibition type using the same constant magnitude relationships as the traditional approach [3].

Diagram 2: Method Comparison - The 50-BOA framework dramatically reduces experimental requirements while maintaining precision.

Experimental Validation and Performance

The 50-BOA methodology has been validated against experimental data for known inhibitor-enzyme pairs, including triazolam-ketoconazole and chlorzoxazone-ethambutol [3]. When applied to these systems, 50-BOA achieved accuracy comparable to conventional comprehensive approaches while demonstrating confidence intervals similar to or narrower than those obtained through traditional methods [34]. This performance confirms that the reduced experimental dataset, when properly selected and analyzed, provides sufficient information for precise parameter estimation without the noise introduced by less informative low-inhibitor concentration data.

The robustness of this approach stems from its theoretical foundation in error landscape analysis, which identified that data from inhibitor concentrations below both Kᵢc and Kᵢu contribute minimal information while introducing estimation sensitivity to measurement errors [34]. By focusing experimental efforts on the maximally informative region of the experimental design space (Iₜ ≥ IC₅₀), the 50-BOA framework achieves superior statistical efficiency. Implementation is supported by publicly available MATLAB and R packages that automate the estimation process, making the methodology accessible to researchers without specialized mathematical expertise [3].

Essential Research Reagent Solutions

Table 3: Key Research Reagents for Enzyme Inhibition Studies

Reagent/Category	Function in Inhibition Analysis	Considerations for Experimental Design
Purified Enzyme Preparations	Catalyzes substrate conversion; target of inhibition studies	Require homogeneity and activity validation; stability assessment critical
Enzyme Substrates	Converted to products; concentration varied to determine kinetics	Should have established Kₘ values; purity affects velocity measurements
Inhibitor Compounds	Bind enzyme to reduce activity; potency quantified by Káµ¢	Solubility limits achievable concentrations; stability in assay buffer
Cofactors (NADPH, etc.)	Enable catalytic activity for certain enzyme classes	Concentration optimization required; stability considerations
Buffer Systems	Maintain optimal pH for enzyme activity	Ionic strength effects on binding; compatibility with detection method
Detection Reagents	Enable quantification of reaction progress	Spectrophotometric, fluorometric, or luminescent detection options
Positive Control Inhibitors	Validate experimental system functionality	Should have well-characterized Káµ¢ values for the target enzyme

This comparative analysis demonstrates that while linear transformation methods provided an historically important tool for enzyme inhibition analysis, their statistical limitations and experimental inefficiencies render them suboptimal for contemporary drug development and biochemical research. The 50-BOA framework represents a paradigm shift in inhibition constant estimation, offering dramatic reductions in experimental requirements while improving estimation precision through principled experimental design and analysis. By leveraging the harmonic mean relationship between ICâ‚…â‚€ and inhibition constants, this approach addresses fundamental identifiability issues that plague traditional methods, particularly for mixed inhibition mechanisms.

The implications for drug discovery and development are substantial, as the 50-BOA methodology can accelerate inhibitor characterization while conserving precious compounds. Future methodological developments will likely build upon this foundation, potentially incorporating optimal experimental design principles for substrate concentration selection and expanding to more complex inhibition mechanisms. As the biochemical community increasingly adopts these efficient, model-informed approaches, the consistency and reliability of enzyme inhibition data across studies should improve significantly, advancing drug development and fundamental enzymology alike.

Optimizing Substrate and Inhibitor Concentration Ranges to Minimize Estimation Bias

Enzyme inhibition analysis serves as a cornerstone in drug development and food processing, providing critical data for predicting metabolic interactions and optimizing therapeutic interventions. The precision of inhibition constant estimation directly impacts the reliability of these predictions, yet traditional experimental approaches often yield inconsistent results across studies due to suboptimal concentration range selection. This comparative analysis examines three methodological frameworks for designing enzyme inhibition experiments: the Canonical Approach, D-Optimum Design, and the novel 50-BOA (IC50-Based Optimal Approach). Each methodology offers distinct strategies for selecting substrate and inhibitor concentration ranges to minimize estimation bias while maximizing experimental efficiency. By objectively comparing these approaches, this guide provides researchers with evidence-based recommendations for selecting appropriate methodologies based on their specific experimental constraints and precision requirements.

Methodological Comparison

Comparative Analysis of Experimental Designs

Table 1: Quantitative Comparison of Enzyme Inhibition Experimental Designs

Experimental Design	Minimum Required Inhibitor Concentrations	Typical Substrate Concentrations	Estimated Experiment Reduction	Key Statistical Advantage
Canonical Approach	4 (0, â…“ICâ‚…â‚€, ICâ‚…â‚€, 3ICâ‚…â‚€)	0.2KM, KM, 5KM	Baseline (0%)	Established empirical foundation
D-Optimum Design	Strategically selected based on parameter space	Optimized across parameter space	~82.5% (120→21 trials)	D-optimum criterion for parameter uncertainty reduction
50-BOA	1 (>ICâ‚…â‚€)	Multiple around KM	>75%	Harmonic mean relationship between ICâ‚…â‚€ and inhibition constants

Theoretical Foundations

Enzyme inhibition kinetics follows established mathematical models where the initial velocity of product formation (Vâ‚€) is described by the equation:

$$V0 = \frac{V{\text{max}}ST}{KM\left(1+\frac{IT}{K{ic}}\right)+ST\left(1+\frac{IT}{K_{iu}}\right)}$$

where S_T, I_T, and E_T denote total substrate, inhibitor, and enzyme concentrations, V_max represents maximal velocity, K_M is the Michaelis-Menten constant, and K_ic and K_iu are the inhibition constants [3]. The relative magnitude of these inhibition constants determines the mechanism: competitive (K_ic << K_iu), uncompetitive (K_iu << K_ic), or mixed inhibition (K_ic ≈ K_iu) [3] [10].

Traditional approaches employ multiple inhibitor concentrations based on estimated ICâ‚…â‚€ values (half-maximal inhibitory concentration) alongside varying substrate concentrations to characterize these parameters [3]. However, recent analyses of error landscapes reveal that nearly half of conventional data points contribute minimally to parameter estimation precision and may introduce bias [3].

Experimental Protocols

Canonical Enzyme Inhibition Protocol

The canonical approach represents the current standard practice in enzyme inhibition studies:

• ICâ‚…â‚€ Determination: Conduct preliminary experiments with a single substrate concentration (typically K_M) across a broad inhibitor concentration range (e.g., 0.001-1000 μM) to estimate ICâ‚…â‚€ [3].

• Experimental Matrix Setup: Establish a full factorial design with substrate concentrations at 0.2K_M, K_M, and 5K_M combined with inhibitor concentrations at 0, â…“ICâ‚…â‚€, ICâ‚…â‚€, and 3ICâ‚…â‚€ [3].

• Velocity Measurements: Measure initial reaction velocities for each concentration combination in appropriate buffer systems with controlled pH and temperature.

• Parameter Estimation: Fit collected velocity data to the appropriate inhibition model using nonlinear regression algorithms to estimate K_ic and K_iu [3].

This approach requires 12 distinct experimental conditions plus approximately 8-12 preliminary trials for ICâ‚…â‚€ determination, totaling 20-24 experimental measurements.

D-Optimum Design Protocol

D-optimum design employs statistical criteria to maximize information gain while minimizing experimental burden:

• Parameter Space Definition: Establish plausible ranges for K_ic, K_iu, and K_M based on literature or preliminary data [46].

• Design Optimization: Calculate D-optimum design points that minimize the determinant of the parameter covariance matrix across the defined parameter space [46].

• Experimental Execution: Conduct measurements at the optimized substrate and inhibitor concentration combinations.

• Iterative Refinement: Optionally refine parameter estimates and experimental design based on initial results.

This methodology demonstrated remarkable efficiency in a practical application, where a D-optimum design with only 21 trials provided comparable parameter estimation precision to a standard design with 120 trials, representing an 82.5% reduction in experimental burden [46].

50-BOA (ICâ‚…â‚€-Based Optimal Approach) Protocol

The 50-BOA method represents a paradigm shift in enzyme inhibition experimental design:

• ICâ‚…â‚€ Determination: Estimate ICâ‚…â‚€ as in the canonical approach using a substrate concentration equal to K_M [3].

• Single Inhibitor Concentration Selection: Choose one inhibitor concentration greater than the estimated ICâ‚…â‚€ value [3].

• Substrate Variation: Measure initial velocities across multiple substrate concentrations (spanning below and above K_M) at the single inhibitor concentration.

• Integrated Analysis: Simultaneously estimate inhibition constants by incorporating the harmonic mean relationship between ICâ‚…â‚€, K_ic, and K_iu during model fitting [3].

This approach reduces the required number of inhibitor concentrations to just one, cutting the total number of experiments by more than 75% compared to conventional methods while improving estimation precision [3] [47].

Figure 1: Experimental Design Workflow Comparison

Research Reagent Solutions

Table 2: Essential Research Reagents for Enzyme Inhibition Studies

Reagent/Category	Specific Examples	Functional Role in Experimentation
Enzyme Systems	Cytochrome P450 (CYP3A4), Acetylcholinesterase, Dihydrofolate reductase	Catalytic targets for inhibition studies; selection depends on research context (drug metabolism, neuroscience, cancer)
Inhibitor Compounds	Ketoconazole, Methotrexate, Ethambutol	Model inhibitors with documented mechanisms; enable experimental validation and method calibration
Substrate Compounds	Midazolam, Triazolam, Chlorzoxazone, Folate	Enzyme-specific substrates converted to measurable products; used at varying concentrations to characterize inhibition
Analytical Tools	Spectrophotometric assays, Fluorescence detection, HPLC-MS	Enable quantification of reaction velocities through product formation or substrate depletion monitoring
Computational Tools	MATLAB 50-BOA package, R statistical package, Nonlinear regression software	Facilitate experimental design optimization and parameter estimation from kinetic data

Results and Comparative Analysis

Estimation Performance Across Methodologies

Table 3: Experimental Data Requirements and Performance Metrics

Performance Metric	Canonical Approach	D-Optimum Design	50-BOA Approach
Minimum Experimental Trials	20-24	21	5-8
Precision (CI Width)	Baseline	Comparable to canonical with 82.5% fewer trials	Improved precision over canonical
Accuracy (Bias)	Potential bias from dispensable data points	Reduced bias through optimal spacing	Minimal bias through error landscape optimization
Prior Knowledge Requirements	ICâ‚…â‚€ estimate	Parameter value ranges	ICâ‚…â‚€ estimate
Inhibition Type Flexibility	All types	Model-dependent	All types without prior knowledge

Error structure analysis reveals that experimental variance in enzyme inhibition studies primarily stems from errors in determining substrate and inhibitor concentrations rather than velocity measurements [48]. This understanding informs the optimization of concentration ranges in the evaluated methodologies.

The 50-BOA approach leverages the insight that experimental data with low inhibitor concentrations (I_T) provides minimal information for estimating inhibition constants [3]. Analysis of error landscapes demonstrates that precise estimation requires I_T > K_ic and/or K_iu, conditions automatically satisfied when using a single inhibitor concentration > ICâ‚…â‚€ [3].

Figure 2: Concentration-Dependent Estimation Bias Relationships

Application Case Studies

Practical validation of the 50-BOA approach demonstrates its effectiveness in real experimental systems:

• Triazolam-Ketoconazole Inhibition: The 50-BOA method provided accurate and precise estimation of inhibition constants for CYP3A4 with substantially reduced experimental requirements compared to conventional approaches [3].

• Chlorzoxazone-Ethambutol Inhibition: Similarly, this system showed comparable parameter estimation performance with reduced experimental burden when applying the 50-BOA methodology [3].

These case studies confirm the practical utility of the optimized concentration range selection in producing reliable inhibition constant estimates while minimizing experimental effort.

This comparative analysis demonstrates that strategic optimization of substrate and inhibitor concentration ranges significantly impacts estimation bias and experimental efficiency in enzyme inhibition studies. The Canonical Approach, while familiar and widely implemented, incorporates nearly 50% dispensable data points that may introduce estimation bias. D-Optimum Design provides substantial efficiency improvements (82.5% reduction in experimental trials) through statistical optimization but requires preliminary parameter range specification. The novel 50-BOA methodology emerges as a superior approach for most scenarios, reducing experimental requirements by >75% while improving estimation precision through strategic use of a single inhibitor concentration >ICâ‚…â‚€ and incorporation of the harmonic relationship between ICâ‚…â‚€ and inhibition constants.

For researchers designing enzyme inhibition studies, the 50-BOA approach offers the most favorable balance of practical implementation, reduced resource requirements, and estimation precision. The availability of user-friendly MATLAB and R packages for implementing 50-BOA further lowers adoption barriers. Future methodological developments will likely build upon these principles of error landscape analysis and strategic concentration range selection to further enhance the efficiency and reliability of enzyme inhibition analysis across diverse application domains.

Enzyme kinetics traditionally focuses on single-substrate reactions following Michaelis-Menten principles. However, many physiological contexts involve multi-enzyme complexes and allosteric regulation that create sophisticated control networks far more complex than simple catalytic models suggest. These systems, where enzymes function as functional heterodimers with both catalytic and allosteric sites, represent a significant challenge for kinetic characterization and inhibitor development [49]. The interplay between multiple substrates competing for both active and allosteric sites, combined with differential allosteric effects, creates a sophisticated regulatory landscape that demands specialized methodological approaches for accurate analysis.

Understanding these complex interactions is particularly crucial in drug discovery, where approximately 47% of all current drugs target enzymes [50]. The limitations of half-maximal inhibitory concentration (IC50) values become particularly apparent in these systems, as they may obscure the true mechanism of inhibition and provide misleading information about compound potency [50]. This comparative analysis examines the experimental challenges, methodological innovations, and strategic approaches for investigating complex enzyme systems, with a focus on generating reliable kinetic parameters for drug development applications.

Multi-Substrate Kinetics and Allosteric Regulation: A Case Study with COX-2

Cyclooxygenase-2 (COX-2) exemplifies the challenges of multi-substrate enzyme kinetics with allosteric regulation. Although structurally a homodimer, COX-2 functions as a functional heterodimer, with one subunit containing the catalytic site and the other an allosteric site [49]. This architecture creates a complex kinetic behavior where substrates can bind to both sites and influence enzyme activity through multiple mechanisms.

Experimental Evidence of Complex Substrate Interactions

Research demonstrates that COX-2 oxygenates both arachidonic acid (AA) and the endocannabinoid 2-arachidonoylglycerol (2-AG) with similar in vitro efficiency, yet cellular biosynthesis of their respective prostaglandin products (PGs and PG-Gs) shows significant disparity [49]. This discrepancy between isolated enzyme kinetics and cellular behavior prompted investigation into more complex regulatory mechanisms.

Table 1: Cellular-Level Modulation of AA and 2-AG Oxygenation in RAW264.7 Cells

Experimental Condition	AA Release	2-AG Release	PG Production	PG-G Production
AA Enrichment	4.2-fold increase	2.4-fold increase	No change	~50% reduction
cPLA2α Inhibition	89% decrease	No change	93% decrease	1.6-fold increase

Cellular studies revealed an inverse correlation between AA levels and PG-G biosynthesis. AA enrichment in RAW264.7 macrophages substantially suppressed PG-G production despite increased 2-AG availability, while pharmacological inhibition of AA release enhanced PG-G biosynthesis [49]. These findings suggested that AA suppresses COX-2-dependent 2-AG oxygenation when both substrates are present.

In Vitro Kinetic Analysis and Mathematical Modeling

In vitro kinetic analysis using purified COX-2 protein demonstrated asymmetric inhibition between substrates. The inhibition of 2-AG oxygenation by high AA concentrations far exceeded the inhibition of AA oxygenation by high 2-AG concentrations [49]. To explain these observations, researchers developed a systems-based mechanistic model that revealed:

• Binding of either AA or 2-AG at the allosteric site decreases catalytic efficiency toward 2-AG
• 2-AG binding at the allosteric site increases catalytic efficiency toward AA
• Substrates interact with COX-2 via multiple potential complexes involving both catalytic and allosteric sites

This model demonstrates how competition combined with differential allosteric modulation creates a complex interplay that preferentially directs COX-2 activity toward AA oxygenation despite similar kinetic efficiency for both substrates in isolation [49].

Figure 1: COX-2 Allosteric Regulation Mechanism. The functional heterodimer architecture allows differential regulation of substrate processing through allosteric binding.

Methodological Innovations in Enzyme Inhibition Analysis

Traditional enzyme inhibition analysis involves experiments with multiple substrate and inhibitor concentrations, but recent advancements have challenged the efficiency and reliability of these conventional approaches.

Limitations of Conventional IC50 Determinations

The relationship between IC50 values and inhibition constants (Ki) varies significantly with inhibition mechanism, which can lead to misinterpretation of inhibitor potency [50]. For competitive inhibitors, IC50 increases with increasing substrate concentration, while for uncompetitive inhibitors, IC50 decreases with increasing substrate concentration. With mixed inhibition, the relationship becomes more complex and depends on the relative magnitudes of the two inhibition constants (Kic and Kiu) [3]. These dependencies mean that IC50 values obtained under limited substrate conditions provide incomplete information about true inhibitor potency and mechanism.

Advanced Approaches for Inhibition Constant Estimation

Recent methodological innovations have addressed these limitations through more efficient experimental designs:

• 50-BOA (IC50-Based Optimal Approach): This method enables precise estimation of inhibition constants using a single inhibitor concentration greater than IC50, substantially reducing the number of required experiments (>75% reduction) while maintaining precision and accuracy [3]. The approach incorporates the harmonic mean relationship between IC50 and inhibition constants into the fitting process.

• One-Step Capillary Electrophoresis Method: This technique enables rapid determination of enzyme kinetics and inhibition constants through improved capillary electrophoresis [18]. The method features a unique injection procedure where substrate and enzyme zones merge during migration, allowing monitoring of the enzymatic reaction in a continuously changing substrate concentration environment.

Table 2: Comparison of Methodological Approaches for Inhibition Constant Determination

Method	Experimental Requirements	Advantages	Limitations
Traditional Multi-Concentration	Multiple substrate and inhibitor concentrations	Comprehensive data set; Well-established	Resource-intensive; Potential for bias
50-BOA Approach	Single inhibitor concentration >IC50	Reduced experiments (>75%); Maintains precision	Requires prior IC50 estimation
One-Step Capillary Electrophoresis	Single CE run with specialized injection	Rapid determination; Minimal reagent use	Specialized equipment required
Multi-Temperature Serial Crystallography	Temperature-controlled SSX experiments	Direct structural insights; Physiological relevance	Technologically complex; Limited accessibility

Multi-Temperature Kinetic Analysis

The recent development of multi-temperature, time-resolved serial crystallography (5D-SSX) enables investigation of enzyme kinetics at physiologically relevant temperatures [51]. This approach addresses the significant limitation that most protein structures are determined at cryogenic temperatures far from physiological conditions, which may obscure crucial conformational states only visible at physiological temperatures.

Application of this methodology to mesophilic β-lactamase CTX-M-14 and thermophilic xylose isomerase demonstrated temperature-dependent modulation of turnover kinetics correlated with structural dynamics observed across a temperature range from below 10°C to above 70°C [51]. These findings highlight how environmental variables like temperature can significantly influence enzyme kinetics and conformational sampling, with important implications for inhibitor design.

Experimental Protocols for Complex Enzyme Systems

Protocol for Assessing Multi-Substrate Competition and Allostery

Based on investigations of COX-2 kinetics [49]:

• Cellular Substrate Modulation:

  • Incubate cells (e.g., RAW264.7 macrophages) with AA complexed to BSA overnight to increase cellular phospholipid AA content by approximately 100%
  • Alternatively, inhibit endogenous AA release using selective cPLA2α inhibitors (e.g., giripladib)
  • Stimulate cells with appropriate agonists (e.g., zymosan, ionomycin)
  • Quantify substrate release and oxygenation products using LC-MS/MS

• In Vitro Kinetic Analysis with Multiple Substrates:

  • Purify target enzyme (e.g., COX-2)
  • Conduct fixed-time point assays (e.g., 10-second incubations) with both substrates present
  • Include hydroperoxide activator (e.g., 1 μM PPHP) to maximize activation while minimizing enzyme self-inactivation
  • Quantify products using specific detection methods (e.g., LC-MS/MS for PG-Gs and PGs)
  • Vary relative concentrations of both substrates to observe competitive interactions

• Mathematical Modeling:

  • Develop unbiased systems-based mechanistic model incorporating all potential enzyme-substrate complexes
  • Use Bayesian parameter inference to determine probability distributions for kinetic constants
  • Validate model against experimental data for both individual and simultaneous substrate oxygenation

Protocol for 50-BOA Inhibition Constant Estimation

Based on the recently developed optimal approach [3]:

• IC50 Determination:

  • Measure % control activity over various inhibitor concentrations with a single substrate concentration (typically at KM)
  • Fit dose-response curve to determine IC50 value

• Experimental Design:

  • Set up reactions at three substrate concentrations: 0.2KM, KM, and 5KM
  • Use a single inhibitor concentration greater than the estimated IC50
  • Measure initial reaction velocities for each condition

• Parameter Estimation:

  • Fit the mixed inhibition equation to the data incorporating the harmonic mean relationship between IC50 and inhibition constants:

    V₀ = (Vₘₐₓ × Sₜ) / [Kₘ(1 + Iₜ/Kᵢ𝒸) + Sₜ(1 + Iₜ/Kᵢᵤ)]

  • Obtain inhibition constants Kᵢ𝒸 and Kᵢᵤ through nonlinear regression

  • Identify inhibition type based on relative magnitudes of Kᵢ𝒸 and Kᵢᵤ

Figure 2: 50-BOA Workflow for Efficient Inhibition Constant Estimation. This optimized approach reduces experimental requirements while maintaining precision.

The Scientist's Toolkit: Essential Research Reagents and Solutions

Table 3: Essential Research Reagents for Complex Enzyme Kinetics Studies

Reagent/Solution	Function/Application	Example Usage
cPLA2α Inhibitors (e.g., giripladib)	Selective inhibition of AA release	Cellular manipulation of AA levels to study substrate competition [49]
Hydroperoxide Activators (e.g., PPHP)	Maximize COX enzyme activation	Short-incubation in vitro assays to minimize enzyme self-inactivation [49]
BSA-Complexed Fatty Acids	Cellular substrate enrichment	Modulating cellular AA content to study impact on alternative substrate metabolism [49]
Stable Isotope-Labeled Standards (e.g., PGE2-G-d5)	Quantification of oxygenation products	LC-MS/MS analysis of prostaglandin and prostaglandin ester products [49]
Capillary Electrophoresis System with adjustable gravity mediation	One-step kinetic determination	Rapid analysis of enzyme kinetics and inhibition constants with minimal reagent use [18]

This comparative analysis demonstrates that navigating complex enzyme kinetics with multi-substrate enzymes and allosteric regulation requires moving beyond traditional kinetic assumptions and methodological approaches. The case of COX-2 illustrates how functional heterodimerism combined with differential allosteric regulation can create sophisticated substrate selectivity mechanisms that are not apparent in single-substrate kinetic analyses.

Methodological innovations such as the 50-BOA approach for efficient inhibition constant estimation and multi-temperature structural kinetics offer powerful tools for addressing these complexities with improved efficiency and physiological relevance. Furthermore, computational approaches that map allosteric networks and predict resistance mutations are increasingly guiding the design of smarter drugs and robust enzymes [52].

For researchers investigating complex enzyme systems, the integration of cellular manipulation, in vitro kinetics, and mathematical modeling provides a comprehensive strategy for elucidating sophisticated regulatory mechanisms. These advanced approaches enable more accurate prediction of cellular behavior from enzymatic parameters and support the development of more effective therapeutic interventions targeting complex enzyme systems.

Evaluating enzyme inhibition is a cornerstone of drug development and fundamental biochemical research. The inhibition constant (Ki), a quantitative measure of an inhibitor's potency, is a critical parameter for predicting drug-drug interactions and understanding enzymatic mechanisms [50]. For decades, the conventional approach to determining Ki has relied on extensive datasets collected from experiments utilizing multiple substrate and inhibitor concentrations. This method, used in over 68,000 studies, demands significant resources of time, materials, and specialized compounds [3]. A persistent challenge for researchers has been to balance the need for precise, reliable data with the practical constraints of experimental efficiency. This guide provides a comparative analysis of traditional and emerging experimental designs for estimating enzyme inhibition constants, offering an objective evaluation of their performance, data requirements, and practical implementation to inform scientific and drug development workflows.

Established Practice: The Conventional Multi-Concentration Approach

The canonical method for enzyme inhibition analysis is characterized by its comprehensive data collection strategy.

Core Protocol and Data Density

The standard protocol is systematic and multi-staged [3]:

• Initial IC50 Estimation: The half-maximal inhibitory concentration (IC50) is first determined by measuring percent control activity across a range of inhibitor concentrations, typically using a single substrate concentration set at the Michaelis constant (KM) [3].
• Matrix-Based Experimental Design: A full factorial experiment is then established using:
  • Substrate concentrations ([S]): Commonly 0.2 KM, KM, and 5 KM.
  • Inhibitor concentrations ([I]): 0, (1/3) IC50, IC50, and 3 IC50.
• Data Fitting: The initial velocity (V0) data collected from all these combinations is fitted to the appropriate inhibition model (e.g., competitive, mixed) to estimate the inhibition constants (Kic and Kiu) [3].

This conventional design generates 12 distinct data points for a single inhibitor, creating a dense dataset intended to fully characterize the inhibition landscape [3].

Performance and Limitations

This method is considered a robust gold standard and can yield accurate estimates when correctly executed. However, its main limitations are resource-related:

• High Experimental Burden: The requirement for multiple substrate and inhibitor concentrations consumes significant amounts of often precious inhibitors and reagents [53].
• Time and Cost Intensity: The numerous experimental conditions translate directly into longer assay times and higher costs.
• Potential for Inefficiency: Recent analyses suggest that nearly half of the conventionally collected data may be dispensable or even introduce bias into the estimation, questioning the efficiency of this data-dense approach [3].

Emerging Efficient Method: The Single High-Concentration Design

A novel methodology, termed the IC50-Based Optimal Approach (50-BOA), challenges the conventional paradigm by drastically reducing experimental workload while maintaining, and sometimes improving, estimation accuracy [3].

Core Protocol and Workflow Efficiency

The 50-BOA protocol integrates the IC50 value into the fitting process itself [3] [34]:

• IC50 Determination: As in the conventional method, the IC50 is first experimentally determined.
• Focused Data Collection: Initial velocity (V0) is measured using a single inhibitor concentration ([I]) that is greater than the determined IC50, across several substrate concentrations.
• Regularized Model Fitting: The data is fitted to the mixed inhibition model while incorporating a regularization term that enforces the known harmonic mean relationship between IC50 and the inhibition constants [3] [34]: Total error = fitting error + λ * ( (IC50 - H(Kic, Kiu)) / IC50 )^2 where H(Kic, Kiu) is the harmonic mean of Kic and Kiu, and λ is a regularization constant determined by cross-validation.

This streamlined design requires only 3 data points (V0 at three substrate concentrations with one [I] > IC50), a 75% reduction in the number of experiments compared to the conventional method [3].

Performance and Advantages

Validation studies indicate that 50-BOA delivers performance on par with or superior to the conventional approach [3] [34]:

• Precision and Accuracy: When applied to real experimental data (e.g., triazolam-ketoconazole and chlorzoxazone-ethambutol inhibition), 50-BOA achieved accuracy comparable to the conventional method, but with confidence intervals that were similar or narrower [3].
• Dramatic Efficiency Gain: The primary advantage is the massive reduction in required experiments (>75%), saving time, resources, and valuable chemical compounds [3] [34].
• Bias Reduction: The method avoids collecting data at low inhibitor concentrations ([I] < min{Kic, Kiu}), which error landscape analysis has shown to be highly sensitive to measurement errors and can introduce bias into the estimation [3] [34].

Table 1: Quantitative Comparison of Experimental Designs for Inhibition Constant (Ki) Estimation

Feature	Conventional Multi-Concentration Design	Single High-Concentration Design (50-BOA)
Typical Data Points Required	12 [3]	3 [3]
Experimental Reduction	Baseline	>75% [3]
Reported Accuracy	High (Gold Standard)	Comparable to Conventional [3] [34]
Reported Precision (CI Width)	Standard	Similar or Narrower than Conventional [3] [34]
Inhibitor Consumption	High	Low
Key Prerequisite	IC50 value	IC50 value & its harmonic mean relationship to Ki [3] [34]
Best Application Context	When substrate/inhibitor resources are abundant	For high-throughput screening or with scarce/expensive compounds

Comparative Analysis of Experimental Protocols

Direct Workflow Comparison

The following diagrams illustrate the fundamental differences in the workflow and data utilization between the two main approaches.

Diagram 1: A comparison of the experimental workflows for the conventional and efficient (50-BOA) approaches, highlighting the significant reduction in experimental steps.

Theoretical Basis for Efficiency: The Error Landscape

The efficiency of the 50-BOA method is rooted in a theoretical analysis of the error landscape for parameter estimation.

Diagram 2: The logical basis for the 50-BOA method. Data from a single high inhibitor concentration is inherently more informative, and its combination with the IC50 constraint allows for a precise fit with minimal data.

The Scientist's Toolkit: Essential Reagent Solutions

Successful execution of enzyme inhibition assays, regardless of the design, relies on key reagents and materials.

Table 2: Key Research Reagent Solutions for Enzyme Inhibition Studies

Reagent / Material	Function in Experiment	Key Considerations
Purified Enzyme Preparation	The biological catalyst whose activity is being measured and inhibited.	Source (recombinant vs. native), specific activity, and purity are critical for reproducible kinetics [54].
Test Inhibitor Compounds	The molecules being evaluated for their potency in reducing enzyme activity.	Solubility (aqueous vs. DMSO stock), stability, and purity are major concerns, especially for novel compounds [53].
Natural Substrate or Probe	The molecule converted by the enzyme to measure catalytic activity.	Should ideally be the natural substrate; probe substrates must be validated. The KM for the substrate must be predetermined [3] [42].
Activity Assay Buffer	Provides the optimal chemical environment (pH, ionic strength, cofactors) for enzyme function.	Must maintain enzyme stability and activity. The choice of container (plastic vs. glass) can affect results due to compound adsorption [54].
Stopped-Flow or Microplate Detection System	Enables rapid, sensitive measurement of initial velocity (Vâ‚€), often via spectrophotometry or fluorescence.	Throughput, sensitivity, and the ability to make rapid measurements are essential for accurate Vâ‚€ determination [42].

The comparative analysis presented in this guide reveals a significant evolution in the experimental design for enzyme inhibition constants. The conventional multi-concentration approach remains a robust, well-understood benchmark. However, the emerging 50-BOA method demonstrates that strategic, model-informed design can achieve comparable—and sometimes superior—precision and accuracy with a fraction of the experimental effort. This efficiency gain is not achieved by simply collecting less data, but by leveraging a deeper understanding of the system's mathematics to collect only the most informative data points.

For the modern researcher, the choice between these protocols depends on context. The conventional method may still be preferred for foundational characterization of a novel enzyme system without prior knowledge. In contrast, the 50-BOA and other efficient methods [53] are exceptionally well-suited for high-throughput screening environments, for working with scarce or expensive inhibitors, and for studies where rapid iteration is key. As the field moves forward, the principles of optimal experimental design are likely to be applied to an even broader range of biological systems, further enhancing the efficiency of drug discovery and biochemical research.

Comparative Validation of Analytical Methods: Selecting the Right Tool for Your Inhibitor

The accurate determination of enzyme inhibition constants (Káµ¢) is a cornerstone of enzymology, with profound implications for drug discovery, development, and safety assessment. Inhibition constants quantify the potency of an inhibitor by representing the dissociation constant for the enzyme-inhibitor complex. Precise and robust estimation of these parameters is essential for predicting drug-drug interactions, optimizing lead compounds, and understanding fundamental enzymatic mechanisms. The experimental landscape for estimating Káµ¢ is populated by several methodological approaches, each with distinct theoretical foundations and practical considerations.

This guide provides a systematic, head-to-head comparison of three methods: the Single Inhibitor Concentration approach based on IC₅₀ (referred to here as SNLR), the estimation of the apparent Michaelis constant (Kₘ,ₐₚₚ), and the Direct Linear Plot (Dixon) method. We objectively evaluate their performance in terms of accuracy, precision, robustness to experimental error, and operational efficiency, providing researchers with the data-driven insights needed to select the optimal method for their specific application.

SNLR (Single Inhibitor Concentration using ICâ‚…â‚€ Relationship)

The SNLR method is a modern, efficient approach that challenges the canonical requirement for multiple inhibitor concentrations. Its core principle is that a precise estimation of inhibition constants is possible using data from a single, optimally chosen inhibitor concentration.

Experimental Protocol [3]:

• ICâ‚…â‚€ Determination: First, the half-maximal inhibitory concentration (ICâ‚…â‚€) is determined from a dataset of percentage control activity versus inhibitor concentration ([I]) at a single substrate concentration, typically near the Kₘ.
• Optimal Single Concentration Selection: The key innovation is the selection of a single inhibitor concentration greater than the estimated ICâ‚…â‚€ for the main experiment. This ensures the data collected is in a high-information region of the error landscape.
• Initial Velocity Measurement: Initial reaction velocities (Vâ‚€) are measured across a range of substrate concentrations at this single, optimal inhibitor concentration.
• Model Fitting with ICâ‚…â‚€ Constraint: The mixed inhibition model (Eq. 1) is fitted to the data, but the relationship between ICâ‚…â‚€, Káµ¢c, and Káµ¢u is incorporated directly into the fitting process. This integration leverages the harmonic mean relationship (ICâ‚…â‚€ ≈ √(Káµ¢c × Káµ¢u)) to stabilize the estimation, allowing for the accurate determination of both inhibition constants from a reduced dataset.

Kₘ,ₐₚₚ (Apparent Michaelis Constant Analysis)

The Kₘ,ₐₚₚ method is a classical, two-stage graphical procedure that relies on analyzing the effect of an inhibitor on the apparent Michaelis-Menten constant.

Experimental Protocol:

• Multi-Concentration Assay: Initial reaction rates are measured across a range of substrate concentrations at several fixed inhibitor concentrations (e.g., 0, â…“ ICâ‚…â‚€, ICâ‚…â‚€, 3 ICâ‚…â‚€) [3].
• Primary Plot and Apparent Constant Estimation: For each inhibitor concentration, the data is plotted (e.g., Lineweaver-Burk, Eadie-Hofstee) and an apparent Kₘ (Kₘ,ₐₚₚ) and apparent Vₘₐₓ (Vₘₐₓ,ₐₚₚ) are determined from the linear fit.
• Secondary Plot for Káµ¢ Estimation: The estimated apparent constants are then re-plotted against the inhibitor concentration. For competitive inhibition, a plot of 1/Vₘₐₓ,ₐₚₚ versus [I] is constructed. The dissociation constant Káµ¢ is determined from the intercept of this secondary plot. A significant limitation is that this method traditionally identifies only a single inhibition constant (Káµ¢c or Káµ¢u) and requires prior knowledge of the inhibition mechanism to select the correct secondary plot.

Dixon (Direct Linear Plot Method)

The Dixon method is a robust, non-parametric graphical technique that uses geometric median statistics for parameter estimation. This guide explores its application to the product competitive inhibition equation in a single stage, avoiding secondary plots.

Experimental Protocol [55]:

• Dataset Creation: Initial reaction rates (vᵢⱼ) are measured for a matrix of substrate concentrations (Sâ±¼) and product/inhibitor concentrations (Páµ¢).
• Triplet Combination and Matrix Solving: The method involves taking all possible combinations of three data points (vᵢⱼ, Sâ±¼, Páµ¢) from the dataset, with the constraint that the three points must not share the same inhibitor concentration. For each triplet, the three parameters (Vₘₐₓ, Kₘ, Kâ‚š) are calculated by solving the corresponding system of three linear equations derived from the rearranged rate equation.
• Median Estimation: The process generates a large list of estimated values for each parameter (e.g., 6,370 estimates from one dataset). The final estimate for each kinetic constant is taken as the median of its respective list. This use of the median makes the method highly robust to outliers and experimental error.

Comparative Performance Analysis

Table 1: Head-to-Head Comparison of Key Characteristics

Feature	SNLR Method	Kₘ,ₐₚₚ Method	Dixon Method
Theoretical Basis	Incorporates ICâ‚…â‚€ relationship into model fitting	Analysis of shifts in apparent constants	Non-parametric geometric median statistics
Experimental Throughput	High (Uses a single inhibitor concentration)	Low (Requires multiple inhibitor concentrations)	Low (Requires a matrix of substrate/inhibitor concentrations)
Prior Knowledge of Mechanism	Not required (Simultaneously estimates Káµ¢c & Káµ¢u)	Required (to choose correct secondary plot)	Not required (Simultaneously estimates constants)
Robustness to Error	High (Optimal design minimizes bias)	Moderate (Error propagates to secondary plot)	Very High (Median is robust to outliers)
Primary Advantage	Drastic reduction in experiments without sacrificing accuracy	Intuitive graphical analysis	Exceptional reliability and resistance to erroneous data points

Quantitative Data on Accuracy and Robustness

The performance of these methods has been quantitatively evaluated through simulation studies and practical applications.

SNLR Performance: The ICâ‚…â‚€-Based Optimal Approach (50-BOA) demonstrates that using a single inhibitor concentration greater than ICâ‚…â‚€ can achieve precision and accuracy comparable to, or even superior than, the canonical multi-concentration approach. This method was successfully validated for estimating the inhibition constants of triazolam-ketoconazole and chlorzoxazone-ethambutol pairs, using substantially less data than conventional methods [3].

Dixon Performance: In a study estimating the product inhibition constant (Kâ‚š) for a competitive inhibition model, the Dixon method was directly compared to the non-linear least squares (LS) method. When error with a variance of 0.01 was introduced to simulated data, the Dixon method produced a lower Sum of Squared Residuals (SSR) in 78-80% of 1,000 experimental runs, demonstrating superior accuracy and robustness. The distribution of Dixon estimates, while broad, centers correctly on the true value, and its median estimator is largely unaffected by outliers [55].

Table 2: Summary of Quantitative Performance Metrics

Method	Statistical Estimator	Robustness to Outliers	Data Efficiency	Key Evidence from Literature
SNLR	Non-linear regression fit	High	>75% reduction in required experiments [3]	Accurate estimation of Káµ¢c and Káµ¢u for mixed inhibition with minimal data [3].
Kₘ,ₐₚₚ	Linear regression fit	Low-Moderate	Low (Requires full dataset)	Standard method; error propagation in secondary plots is a known limitation.
Dixon	Median	Very High	Low (Requires full dataset)	Lower SSR than LS methods under error; reliable Kâ‚š estimation from a single dataset [55].

Experimental Workflow and Signaling Pathways

The following diagram illustrates the core logical workflow and decision-making process for selecting and applying the three compared methods.

The Scientist's Toolkit: Essential Research Reagents and Materials

Table 3: Key Reagent Solutions for Enzyme Inhibition Studies

Item	Function in Analysis	Specific Example / Consideration
Purified Enzyme	The biological catalyst under investigation; source and purity are critical for reproducible kinetics.	Recombinant human Cytochrome P450 enzymes (e.g., CYP3A4) for drug metabolism studies.
Substrate	The molecule transformed by the enzyme; chosen based on known enzyme activity.	Midazolam or triazolam for CYP3A4 inhibition assays [3].
Inhibitor	The compound being evaluated for its ability to reduce enzymatic activity.	Ketoconazole (strong CYP3A4 inhibitor) for constant estimation [3].
Reaction Buffer	Provides the optimal chemical environment (pH, ionic strength) for enzyme activity.	Phosphate or Tris buffer at the enzyme's optimal pH.
Cofactor Systems	Supplies essential non-protein components for enzymatic reactions.	NADPH-regenerating system for oxidoreductases like P450s.
Detection Reagents	Enable quantification of the initial reaction rate (Vâ‚€).	Fluorescent or luminescent probes, or reagents for stopped-colorimetric assays.

The comparative analysis reveals a clear trade-off between experimental efficiency and inherent robustness, guiding method selection based on project goals.

For high-throughput environments, such as early-stage drug screening where rapid triage of compounds is essential, the SNLR method is transformative. Its ability to deliver accurate estimates of both competitive and uncompetitive inhibition constants with a drastic reduction in experimental workload offers a significant advantage. The Dixon method remains the gold standard for reliability when data quality is uncertain or when analyzing a critical compound where robustness is paramount. Its median-based estimation provides confidence that the result is not skewed by a few erroneous measurements. The traditional Kₘ,ₐₚₚ method, while intuitive and historically important, is outperformed in both efficiency and robustness by the modern alternatives discussed. Its requirement for prior mechanistic knowledge and susceptibility to error propagation are notable limitations.

In conclusion, there is no single "best" method for all scenarios. The choice between SNLR, Kₘ,ₐₚₚ, and Dixon should be guided by the specific context:

• Choose SNLR (50-BOA) for maximum efficiency and high-throughput needs.
• Choose the Dixon method for maximum robustness and reliability with limited dataset sizes.
• The Kₘ,ₐₚₚ method is best suited for educational purposes or when corroborating results from other methods.

Evaluating Computational and In Silico Methods for Ki Prediction in Early Drug Design

The precise prediction of enzyme inhibition constants, particularly the dissociation constant (Ki), is a cornerstone of early drug discovery. Accurate Ki values are critical for evaluating a compound's potency, understanding its mechanism of action, and predicting potential drug-drug interactions. Traditionally, Ki determination has relied on extensive in vitro experiments, which are resource-intensive and low-throughput. This guide provides a comparative analysis of computational and in silico methods for Ki prediction, examining their underlying principles, data requirements, and performance to inform their application in modern drug development pipelines.

Computational approaches for predicting drug-target interactions and inhibition constants have evolved significantly, ranging from classical techniques based on physical principles to modern data-driven models.

Table 1: Comparison of Key Ki Prediction Methodologies

Method Category	Representative Methods	Underlying Principle	Typical Data Requirements	Key Advantages	Major Limitations
Structure-Based	Molecular Docking (e.g., HADDOCK, IDOCK) [56] [57]	Simulates binding pose and affinity using 3D protein structures.	High-resolution protein structures (e.g., from X-ray, NMR, or AlphaFold).	Provides mechanistic insight into binding interactions.	Accuracy hinges on precise protein structures and force fields.
Ligand-Based	QSAR, Pharmacophore Models [56]	Infers activity from known bioactive compounds using chemical similarity.	Libraries of compounds with known activity values (e.g., Ki, IC50).	Effective when protein structure is unknown.	Cannot explore novel chemical spaces beyond training data.
Machine Learning (ML)	KronRLS, SimBoost, DGraphDTA [56]	Learns complex patterns from data on drug and target features.	Large, high-quality datasets of drug-target pairs and affinities.	Can model non-linear relationships; high potential accuracy.	Performance depends on data quality and volume; "black box" nature.
Hybrid/Network-Based	DTINet, BridgeDPI [56]	Integrates diverse biological data (e.g., genomics, side effects) using network theory.	Heterogeneous data from multiple sources (drugs, proteins, diseases).	Can leverage "guilt-by-association"; robust to sparse data.	Complex integration pipelines; potential for propagated noise.
Experiment-Informed Computation	50-BOA, Guided Docking, ENSEMBLE [3] [57]	Uses experimental data to constrain or validate computational models.	Initial experimental data (e.g., IC50, reaction velocity).	Increases reliability and interpretability of predictions.	Still requires some initial experimental effort.

A critical development in the field is the 50-BOA (IC50-Based Optimal Approach), a method that efficiently bridges experimental and computational work. This approach leverages the relationship between the half-maximal inhibitory concentration (IC50) and inhibition constants (Ki). By incorporating this relationship into the model fitting process, 50-BOA allows for precise estimation of Ki using data from a single inhibitor concentration greater than the IC50, substantially reducing the number of required experiments by over 75% compared to conventional methods [3].

Experimental Protocols and Workflows

Understanding the standard experimental protocols is essential for developing and validating computational models, as these assays generate the ground-truth data used for training and testing.

Conventional Enzyme Inhibition Assay

The canonical experimental method for determining Ki involves measuring the initial velocity of an enzyme-catalyzed reaction under various conditions [3]. The standard protocol is as follows:

• IC50 Estimation: The half-maximal inhibitory concentration (IC50) is first determined by measuring the percentage of control enzyme activity across a range of inhibitor concentrations, typically using a single substrate concentration at the Michaelis-Menten constant (KM) [3].
• Experimental Design: A matrix of experiments is established using substrate concentrations (ST) at 0.2KM, KM, and 5KM, and inhibitor concentrations (IT) at 0, (1/3)IC50, IC50, and 3IC50 [3].
• Velocity Measurement: For each combination of ST and IT, the initial reaction velocity (V0) is measured.
• Model Fitting and Ki Estimation: The general mixed inhibition model (Equation 1) is fitted to the velocity data to estimate the inhibition constants Kic and Kiu, which characterize the inhibitor's binding affinity to the enzyme and the enzyme-substrate complex, respectively [3].

Equation 1: General Mixed Inhibition Model

The following workflow diagram illustrates the key decision points in selecting a Ki prediction strategy, highlighting the role of the modern 50-BOA method:

Benchmarking and Validation Frameworks

Rigorous benchmarking is vital for assessing the real-world performance of computational models. The CARA (Compound Activity benchmark for Real-world Applications) benchmark addresses this need by distinguishing between two primary drug discovery tasks [58]:

• Virtual Screening (VS) Assays: Simulate the hit identification stage, containing compounds with low pairwise similarities from diverse chemical libraries.
• Lead Optimization (LO) Assays: Simulate the hit-to-lead stage, containing series of congeneric compounds with high structural similarity.

CARA employs tailored train-test splitting schemes for these tasks to prevent over-optimistic performance estimates and to ensure models are evaluated on realistic data distributions, including "cold-start" scenarios where no task-specific data is available (zero-shot) or very little is available (few-shot) [58].

Performance Comparison and Analysis

Evaluations on benchmarks like CARA reveal that the performance of computational methods is not uniform and depends heavily on the specific task and data availability.

Table 2: Performance Analysis of Ki Prediction Strategies

Method Category	Reported Strengths	Identified Challenges & Contextual Performance	Suitability for Discovery Stage
Structure-Based	Provides mechanistic insight; does not require prior activity data.	Performance highly dependent on accuracy of protein structure and scoring functions.	Hit Identification, Lead Optimization
Ligand-Based	Fast and effective when similar active compounds are known.	Limited ability to explore novel chemical space; fails for new scaffolds.	Hit Identification
Machine Learning (ML)	Can capture complex, non-linear structure-activity relationships.	Performance varies across different assays [58]; requires large, high-quality training data; risk of poor generalizability.	Hit Identification, Lead Optimization
Hybrid/Network-Based	More robust to sparse data; can suggest off-target effects.	Complex to implement and validate; integration of noisy data is challenging.	Hit Identification
Experiment-Informed 50-BOA	Reduces experimental burden by >75%; ensures precision and accuracy [3].	Requires initial, single IC50 value for a given inhibitor.	Lead Optimization

A significant finding from recent studies is that popular training strategies like meta-learning and multi-task learning can improve model performance for Virtual Screening (VS) tasks. In contrast, for Lead Optimization (LO) tasks involving congeneric series, training standard QSAR models on separate assays often already yields decent results [58]. This underscores the importance of matching the computational strategy to the specific application context within the drug discovery pipeline.

The Scientist's Toolkit: Essential Research Reagents and Solutions

Successful implementation of computational predictions often relies on integration with experimental biology. The following table details key reagents and tools used in the field.

Table 3: Key Research Reagent Solutions for Enzyme Inhibition Analysis

Reagent / Material	Function in Inhibition Analysis	Example Context
Cytochrome P450 (CYP) Enzymes	Key drug-metabolizing enzymes whose inhibition is a major clinical concern for drug-drug interactions.	Used as target proteins in inhibition studies to predict metabolic risks [3].
Sodium Dodecyl Sulfate (SDS)	Dispersing agent used to homogenize carbon nanotubes and other nanomaterials in aqueous solution.	Used in composite material preparation to ensure even distribution of nanotubes [59].
Carbon Nanotubes (CNT)	Nanomaterials with excellent mechanical properties; used experimentally in novel composite materials.	Studied as inclusions in cement paste to enhance mechanical performance [59].
ChEMBL Database	A manually curated database of bioactive molecules with drug-like properties, providing Ki, IC50, and other bioactivity data.	Serves as a primary public resource for obtaining compound activity data to train and validate predictive models [58].
BindingDB & PubChem	Public databases providing access to massive amounts of experimental compound activity and binding data.	Used as resources for large-scale, high-quality compound activity datasets for model training [58].

This guide has objectively compared the landscape of computational methods for Ki prediction, from classical docking to innovative hybrid approaches like the experiment-informed 50-BOA. The key insight is that there is no single superior method; each approach offers distinct trade-offs in accuracy, data dependency, and applicability across virtual screening and lead optimization tasks. The emergence of robust benchmarks like CARA and efficient protocols like 50-BOA signifies a move toward more reliable and practical in silico tools. For researchers, the optimal strategy involves a judicious combination of these computational methods with targeted experimental validation, ensuring that Ki prediction continues to enhance the efficiency and success of early drug design.

The accurate determination of enzyme inhibition constants (Ki) is a cornerstone of drug development, food processing, and clinical toxicology risk assessment [3] [24]. These constants quantify inhibitor potency and elucidate the mechanism of action, directly informing drug dose adjustments and the management of drug-drug interactions. Traditionally, estimating these parameters has been a resource-intensive process, requiring initial IC50 determination followed by velocity measurements across multiple substrate and inhibitor concentrations [3]. This conventional approach consumes significant quantities of often scarce compounds and requires substantial experimental time.

Recent methodological advances challenge this paradigm by offering streamlined pathways to precise Ki estimation. This guide provides a comparative analysis of established and emerging experimental approaches, evaluating them against the critical criteria of throughput, precision, and resource requirements to aid researchers in selecting the optimal methodology for their specific context.

Performance Comparison of Methodologies

The table below provides a systematic comparison of three distinct approaches for inhibition constant determination, summarizing their key performance characteristics and optimal use cases.

Table 1: Comparative Analysis of Enzyme Inhibition Constant Determination Methods

Method	Throughput & Experimental Load	Precision & Accuracy	Resource Requirements	Key Advantages	Key Limitations
Canonical (Traditional) Approach	Low throughput; Requires initial IC50 estimation followed by velocity measurements at 3 substrate concentrations (e.g., 0.2Km, Km, 5Km) and 4 inhibitor concentrations (e.g., 0, 1/3 IC50, IC50, 3 IC50) [3]	Can be precise for competitive/uncompetitive inhibition; Prone to bias and inconsistency for mixed inhibition [3]	High consumption of inhibitors and substrates; Labor-intensive	Comprehensive data collection; Well-established protocol	Nearly half of conventional data may be dispensable and introduce bias [3]
50-BOA (IC50-Based Optimal Approach)	Very high throughput; Requires data at a single inhibitor concentration > IC50 with multiple substrate concentrations [3]	High precision and accuracy; Dramatically improved confidence intervals for mixed inhibition constants [3]	Reduces number of experiments by >75% [3]; User-friendly MATLAB/R packages available	Eliminates need for prior knowledge of inhibition type; Optimal for mixed inhibition studies	Requires initial IC50 estimate; Single inhibitor concentration must be carefully chosen
Efficient Screening Approach (for Transporters)	High throughput screening; Ki estimation from a single data point using inhibitor concentration of 10×Kt (potent inhibitors) or 100×Kt (non-potent inhibitors) [53]	Accurate Ki estimation validated across multiple solute carrier transporters [53]	Minimal compound consumption; Accommodates low-solubility compounds	Rapid screening capability; Resource-efficient for early-stage discovery	Primarily validated for transporter studies; May require adaptation for enzyme targets

Detailed Experimental Protocols

Canonical (Traditional) Approach

The conventional method for estimating inhibition constants follows a well-established multi-step protocol [3]:

• IC50 Determination: Perform initial experiments to determine the half-maximal inhibitory concentration (IC50) by measuring percentage control activity across a range of inhibitor concentrations, typically using a single substrate concentration set at the Michaelis-Menten constant (Km) [3].

• Experimental Design: Establish a matrix of experimental conditions using:

  • Substrate concentrations: 0.2Km, Km, and 5Km
  • Inhibitor concentrations: 0, (1/3)IC50, IC50, and 3IC50 [3]

• Velocity Measurement: For each combination of substrate and inhibitor concentrations, measure the initial velocity of the enzymatic reaction (V0).

• Model Fitting: Fit the general mixed inhibition model (Equation 1) to the complete dataset to estimate the inhibition constants Kic and Kiu, and identify the inhibition type.

  Equation 1 (General Mixed Inhibition Model): V0 = (Vmax × ST) / [ Km × (1 + IT/Kic) + ST × (1 + IT/Kiu) ] [3]

50-BOA (IC50-Based Optimal Approach) Protocol

The novel 50-BOA method streamlines the traditional process [3]:

• Preliminary IC50 Estimation: As in the canonical approach, first determine the IC50 value using a single substrate concentration at Km.

• Optimized Experimental Design:

  • Select a single inhibitor concentration greater than the estimated IC50.
  • Measure initial reaction velocities across a range of substrate concentrations at this single inhibitor level.

• Integrated Model Fitting: Estimate the inhibition constants by fitting the mixed inhibition model (Equation 1) to the data, while incorporating the known harmonic mean relationship between IC50 and the inhibition constants (Kic and Kiu) directly into the fitting process. This integration is key to achieving high precision with minimal data [3].

Single-Point Screening Protocol for Transporters

This efficient approach, validated for solute carrier transporters, enables Ki estimation from minimal data [53]:

• Substrate Affinity Determination: First, determine the substrate's transport affinity constant (Kt) for the target transporter.

• Inhibitor Concentration Selection:

  • For potent inhibitors (anticipated Ki < 20×Kt): Use a single inhibitor concentration of 10×Kt.
  • For non-potent inhibitors (anticipated Ki > 20×Kt): Use a single inhibitor concentration of 100×Kt.

• Uptake Measurement: Measure substrate uptake (e.g., radiolabeled taurocholate for ASBT) in the presence and absence of the selected single inhibitor concentration.

• Ki Calculation: Analyze the inhibition data using the appropriate model (e.g., Michaelis-Menten competitive inhibition model) to calculate the Ki value from the single data point [53].

Workflow and Logical Relationships

The following diagram illustrates the logical sequence and key decision points for selecting and applying the different methodologies for inhibition constant determination.

The Scientist's Toolkit: Essential Research Reagents and Materials

Successful execution of enzyme inhibition studies requires careful selection of reagents and materials. The following table outlines key solutions and their critical functions in the experimental workflow.

Table 2: Essential Research Reagent Solutions for Enzyme Inhibition Studies

Reagent/Material	Function in Experiment	Application Notes
Enzyme Preparations	Biological catalyst for the reaction being inhibited; source of inhibition binding sites	Purity and specific activity must be consistent; recombinant enzymes often used for standardization [60]
Inhibitor Compounds	Test molecules whose binding affinity and mechanism are being characterized	Aqueous solubility can be a limiting factor; DMSO stocks (1-2.5%) often used with controls for solvent effects [53]
Natural Substrates	Native molecules transformed by the enzyme in the catalytic process	Preferred over artificial analogs for physiological relevance; concentration ranges should span Km [60]
Detection Systems	Enable measurement of reaction velocity and inhibitor potency	Label-free calorimetric (e.g., Enthalpy Arrays) and radiometric/scintillation detection are common [60] [53]
IC50 Determination Buffer	Medium for initial inhibitor potency assessment	Typically uses single substrate concentration at Km [3]
Velocity Assay Buffer	Environment for detailed kinetic parameter estimation	Must maintain enzyme stability and activity; ion composition critical for metalloenzymes [60]

The landscape of enzyme inhibition analysis is evolving toward more efficient and precise methodologies. The traditional canonical approach, while comprehensive, has been shown to potentially generate dispensable data and introduce bias, particularly for mixed inhibition studies [3]. Emerging methods like the 50-BOA demonstrate that incorporating biochemical relationships (e.g., the harmonic mean between IC50 and Ki) into the fitting process enables precise estimation with a single, well-chosen inhibitor concentration, reducing experimental load by over 75% [3]. For high-throughput screening environments, particularly in transporter studies, single-point methods provide a valuable balance between resource conservation and acceptable accuracy [53].

Method selection should be guided by the specific research context: the 50-BOA is optimal for precise mixed inhibition constant estimation without prior knowledge, single-point screening excels in early-stage discovery, and the canonical approach may remain valuable for standardized confirmation studies. By aligning methodological strengths with project goals, researchers can significantly enhance the efficiency and reliability of enzyme inhibition analysis in drug development and related fields.

Within drug discovery, the accurate determination of enzyme inhibition constants (Káµ¢) is a critical step in assessing the potency and mechanism of potential therapeutic compounds. These constants serve as fundamental metrics for ranking lead compounds, predicting in vivo efficacy, and ultimately, for regulatory submissions. However, the journey from experimental data to regulatory acceptance is fraught with challenges, including experimental variability, computational model inaccuracies, and the use of non-standardized benchmarks. This guide provides a comparative analysis of current gold standards and validation protocols essential for robust enzyme inhibitor characterization. It objectively compares emerging benchmarking datasets, innovative experimental methods, and computational validation approaches, providing a structured framework for researchers to validate their experimental and in silico protocols against community-accepted standards, thereby strengthening the evidence required for successful regulatory applications.

Gold Standard Datasets for Virtual Screening

The foundation of any reliable computational model is its training and validation on high-quality, robustly curated datasets. Traditionally, benchmarks like MoleculeNet and Therapeutics Data Commons (TDC) have been used, but these often suffer from issues such as inconsistent chemical representations, undefined stereochemistry, and noisy experimental data [61]. To address these limitations, the WelQrate dataset collection has been introduced as a new gold standard for small molecule drug discovery benchmarking [61].

The WelQrate Benchmarking Standard

WelQrate is a meticulously curated collection of nine datasets spanning five therapeutic target classes, including G-protein coupled receptors (GPCRs) and ion channels [61]. Its hierarchical curation pipeline, designed by drug discovery experts, goes beyond primary high-throughput screens (HTS) by incorporating confirmatory and counter-screens to ensure high data quality and reliability [61]. The table below summarizes the key characteristics of the datasets within the WelQrate collection.

Table 1: Overview of WelQrate Dataset Collection for Benchmarking

Target Class	Target	BioAssay AID	Compound Type	Total Compounds	Number of Actives	Hit Rate
GPCR	Orexin 1 Receptor	435008	Antagonist	307,660	176	0.057%
GPCR	M1 Muscarinic Receptor	1798	Allosteric Agonist	60,706	164	0.270%
GPCR	M1 Muscarinic Receptor	435034	Allosteric Antagonist	60,359	78	0.129%
Ion Channel	Potassium Ion Channel Kir2.1	1843	Inhibitor	288,277	155	0.054%
Ion Channel	KCNQ2 Potassium Channel	2258	Potentiator	289,068	247	0.085%
Ion Channel	Cav3 T-type Calcium Channel	463087	Inhibitor	95,650	652	0.682%

The curation process employs rigorous domain-driven preprocessing, including Pan-Assay Interference Compounds (PAINS) filtering, to remove promiscuous compounds that could lead to false positives [61]. The collection provides data in multiple standardized formats, including isomeric SMILES (which preserves stereochemistry), InChI, SDF, and 2D/3D graphs, facilitating a common ground for fair and comprehensive benchmarking [61].

Experimental Validation of Gold Standard Inhibitors

Beyond dataset curation, the experimental validation of ultra-potent inhibitors against high-resolution structures provides a different form of gold standard. The following table lists several well-characterized protease-inhibitor complexes with femtomolar to picomolar affinity, which serve as excellent reference points for validating both experimental and computational methods.

Table 2: Experimentally Validated High-Potency Protease Inhibitors as Gold Standards

Protease/Inhibitor Complex	Experimental Kᵢ	Calculated ΔG (kJ/mol)	PDB ID
β-Trypsin / BPTI	0.00006 nM	-75.43	2PTC
α-thrombin / hirudin-v2	0.000022 nM	-77.91	4HTC
β-Trypsin / SFTI-1	0.017 nM	-61.47	1SFI
KLK4 / SFTI-F2Q4R5N14	0.039 nM	-59.40	4KEL
Matriptase / SFTI-1	0.92 nM	-51.55	3P8F

These complexes, with their precisely measured inhibition constants and available 3D structures, provide an invaluable benchmark for validating computational methods that predict binding affinity, such as free energy calculations and molecular docking scoring functions [62].

Experimental Protocols for Inhibition Constant Determination

The 50-BOA: A Novel Protocol for Efficient Káµ¢ Estimation

A recent groundbreaking study published in Nature Communications (2025) introduces the "50-BOA" (ICâ‚…â‚€-Based Optimal Approach), a protocol that substantially reduces the experimental burden of inhibition constant estimation while improving precision and accuracy [3].

The traditional, or canonical, approach for estimating inhibition constants involves measuring initial reaction velocities across multiple substrate concentrations (e.g., 0.2Kₘ, Kₘ, 5Kₘ) and multiple inhibitor concentrations (e.g., 0, ¹/₃IC₅₀, IC₅₀, 3IC₅₀) [3]. The 50-BOA protocol simplifies this significantly. Error landscape analysis revealed that nearly half of the conventional data is dispensable and can even introduce bias [3]. Instead, by incorporating the relationship between IC₅₀ and the inhibition constants (Kᵢc and Kᵢu) into the fitting process, precise and accurate estimation is possible using a single inhibitor concentration greater than the IC₅₀ [3].

The following diagram illustrates the workflow of this optimized protocol.

Diagram 1: The 50-BOA workflow for Ki estimation

This approach reduces the number of required experiments by more than 75% while ensuring precision and accuracy, offering a highly efficient method for drug developers [3]. The authors provide a user-friendly package that implements the 50-BOA for broader adoption [3].

Critical Considerations in Káµ¢ Determination

While protocols like 50-BOA enhance efficiency, the reliability of any Káµ¢ value is contingent on meticulous experimental conduct. Several factors, if overlooked, can severely compromise results:

• Nontarget Site Interactions: The experimentally determined Káµ¢ can be dramatically affected by seemingly trivial factors such as the choice of container material. For instance, the adsorption of bis(7)-tacrine to glass containers increased its Káµ¢ against acetylcholinesterase to 3.2 nM, compared to 2.9 pM measured in plastic containers—a change of over 1000-fold [54].
• Enzyme Purity: The presence of inactive enzyme can serve as a nonspecific "sink" for inhibitors. A study showed that as the specific activity of acetylcholinesterase decreased, the apparent Káµ¢ for bis(7)-tacrine increased from 2.9 pM to 734 pM due to binding to the inactive enzyme [54].
• Bioanalytical Validation: For regulatory submissions, bioanalytical methods must be rigorously validated. The European Medicines Agency (EMA) requires Incurred Sample Reanalysis (ISR) to demonstrate the reliability of the analytical method used in pharmacokinetic studies. A scientific justification is required if ISR is not performed, which is scrutinized on a case-by-case basis [63].

Computational Validation and Benchmarking

Benchmarking Scoring Functions with WelQrate

The WelQrate evaluation framework provides a standardized model evaluation framework that considers high-quality datasets, featurization methods, 3D conformation generation, evaluation metrics, and data splits [61]. This framework allows for the reliable benchmarking of virtual screening algorithms, which is crucial for regulatory acceptance of in silico models. Using such a standardized benchmark helps to objectively compare the performance of different computational models and scoring functions, identifying those most suitable for predicting compound activity in a real-world drug discovery context.

Machine Learning Potentials and Free Energy Calculations

Beyond traditional docking, machine learning (ML) potentials are emerging as powerful tools for predicting binding affinities. The ANI-ML potential, for example, has been benchmarked as a rescoring function in molecular docking [64]. On the CASF-2016 benchmark, ANI was ranked in the top 5 among 34 tested scoring functions, demonstrating its "docking power" [64]. When used in conjunction with the GOLD-PLP scoring function, ANI can boost the top-ranked solution to be the closest to the X-ray structure [64].

A robust virtual screening protocol may involve consensus scoring, combining docking scores from ANI and GOLD with more sophisticated but computationally expensive free energy methods like MM-PBSA and ANI_LIE [64]. This multi-stage approach allows for the efficient screening of ultra-large libraries while maintaining high accuracy.

Predicting Káµ¢ from Structural Data

For experimentally characterized structures, computational methods can provide theoretical Kᵢ values that complement experimental data. A relatively simple yet effective approach uses the YASARA plugin FoldX and the PRODIGY web server to calculate free binding energies (ΔG) from protein-inhibitor complex structures (PDB coordinates) [62]. The calculated ΔG values are then converted to Kᵢ using the fundamental relationship derived from the Van 't Hoff equation: K = exp(ΔG/RT), where K is the equilibrium constant (Kᵢ for competitive inhibition is interpreted as a dissociation constant, K_D) [62].

This workflow has shown good correlation with empirical data, particularly for serine proteases, providing researchers with a valuable tool for initial potency assessments and for rationalizing the design of more potent inhibitor variants [62].

The Scientist's Toolkit: Essential Research Reagent Solutions

The following table details key reagents, resources, and software essential for conducting rigorous enzyme inhibition studies and validation protocols.

Table 3: Essential Research Reagent Solutions for Inhibition Studies

Item/Tool	Type	Primary Function	Example/Source
WelQrate Dataset Collection	Benchmarking Data	Provides gold-standard, publicly available datasets for benchmarking virtual screening algorithms.	WelQrate.org [61]
50-BOA Implementation	Software Package	Automates the estimation of inhibition constants using the efficient single-inhibitor concentration protocol.	MATLAB/R package [3]
FoldX (YASARA Plugin)	Software	Analyzes protein stability and protein-inhibitor binding affinities to calculate theoretical Káµ¢ from PDB structures.	YASARA Suite [62]
PRODIGY Web Server	Web Service	Predicts protein-inhibitor binding affinities (KD) using machine learning algorithms.	PRODIGY Server [62]
ANI-ML Potentials	Software (ML Potentials)	Serves as a fast and accurate scoring function for rescoring docking poses and calculating interaction energies.	ANI-2x [64]
High-Potency Reference Inhibitors (e.g., BPTI, Hirudin)	Biological Reagents	Serve as gold-standard positive controls for inhibitor potency and computational method validation.	Commercial Suppliers [62]
Pan-Assay Interference Compounds (PAINS) Filters	Computational Filter	Identifies and removes promiscuous compounds that can cause false positives in HTS.	Implemented in WelQrate [61]

The path to regulatory submission for enzyme inhibitors demands rigorous validation against gold standards. This guide has outlined a comprehensive framework, from leveraging next-generation benchmarking datasets like WelQrate and adopting highly efficient experimental protocols like the 50-BOA, to implementing robust computational validation using ML potentials and free energy calculations. A critical finding for drug developers is that mixed inhibition, one of the most commonly encountered mechanisms, is frequently misinterpreted. Statistical analysis confirms that it predominantly arises from inhibitors binding exclusively to the enzyme's active site, rather than to both active and allosteric sites as often assumed [15]. This clarification is essential for the rational design of inhibitors. By integrating these standardized protocols, benchmark datasets, and a clear understanding of inhibition mechanisms, researchers can generate the high-quality, reproducible data necessary to build a compelling case for regulatory approval.

Conclusion

The comparative analysis of methods for determining enzyme inhibition constants reveals a clear trajectory from traditional, error-prone linearizations toward more robust, efficient computational and nonlinear regression techniques. The foundational understanding of Ki and IC50 remains paramount, but methodological advancements like Simultaneous Nonlinear Regression (SNLR) and novel approaches such as the 50-BOA method now enable greater precision with reduced experimental burden. For drug development professionals, this evolution means that reliable Ki determination is more accessible, facilitating the accelerated design of high-potency, selective enzyme inhibitors. Future directions will likely involve greater integration of in silico predictions with high-throughput experimental validation, further embedding precise inhibition kinetics into the backbone of rational drug design for complex diseases ranging from neurodegeneration to oncology.

References

• 1. What is the difference between Ki and IC50 in enzyme ... [https://www.aatbio.com/resources/faq-frequently-asked-questions/What-is-the-difference-between-Ki-and-IC50-in-enzyme-inhibition]
• 2. The difference between Ki, Kd, IC50, and EC50 values [https://www.sciencesnail.com/science/the-difference-between-ki-kd-ic50-and-ec50-values]
• 3. Optimizing enzyme inhibition analysis: precise estimation ... [https://www.nature.com/articles/s41467-025-60468-z]
• 4. IC50 [https://en.wikipedia.org/wiki/IC50]
• 5. The power issue: determination of KB or Ki from IC50: A ... [https://www.sciencedirect.com/science/article/abs/pii/S1056871902001661]
• 6. The Reliability of Estimating Ki Values for Direct, ... [https://pubmed.ncbi.nlm.nih.gov/26354951/]
• 7. IC50 to Ki Converter Tool | HSLS [https://www.hsls.pitt.edu/obrc/index.php?page=URL1253895599]
• 8. Competitive Inhibition [https://chem.libretexts.org/Courses/CSU_Chico/CSU_Chico%3A_CHEM_451_-_Biochemistry_I/CHEM_451_Test/08%3A_Transport_and_Kinetics/8.4%3A_Enzyme_Inhibition/Competitive_Inhibition]
• 9. Competitive inhibition [https://en.wikipedia.org/wiki/Competitive_inhibition]
• 10. 5.4: Enzyme Inhibition [https://chem.libretexts.org/Courses/University_of_Arkansas_Little_Rock/CHEM_4320_5320%3A_Biochemistry_1/05%3A_Michaelis-Menten_Enzyme_Kinetics/5.4%3A_Enzyme_Inhibition]
• 11. Physiology, Noncompetitive Inhibitor - StatPearls - NCBI - NIH [https://www.ncbi.nlm.nih.gov/books/NBK545242/]
• 12. Non-competitive inhibition [https://en.wikipedia.org/wiki/Non-competitive_inhibition]
• 13. Equation: Noncompetitive inhibition [https://www.graphpad.com/guides/prism/latest/curve-fitting/reg_noncompetitive_inhibition.htm]
• 14. A mechanism of uncompetitive inhibition of the serotonin ... [https://elifesciences.org/articles/82641]
• 15. Mixed and non-competitive enzyme inhibition - PubMed Central [https://pmc.ncbi.nlm.nih.gov/articles/PMC10683834/]
• 16. Cheng-Prusoff Equation [https://pharmacologycanada.org/Cheng-Prusoff-equation]
• 17. Ki to IC50 Converter - Punnett Square Calculator [https://punnettsquare.org/ki-to-ic50-converter/]
• 18. One-step method for rapid determination of enzyme ... [https://www.sciencedirect.com/science/article/abs/pii/S0026265X25016224]
• 19. Evaluation of various experimental conditions and ... [https://www.sciencedirect.com/science/article/abs/pii/S0090955625091263]
• 20. Using Dixon Plot for Enzyme Inhibition: Correct Axes Selection ... [https://www.letstalkacademy.com/dixon-plot-enzyme-inhibition-1-over-v-vs-inhibitor-concentration/]
• 21. A practical guide for the assay-dependent characterisation ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11544421/]
• 22. Methods for kinetic evaluation of reversible covalent inhibitors ... [https://pubs.rsc.org/en/content/articlehtml/2025/md/d5md00050e]
• 23. Advances in Xanthine Oxidase Inhibition: A Review of ... [https://pubmed.ncbi.nlm.nih.gov/40838763/]
• 24. enzyme kinetics, and in vitro-to-in vivo scaling models [https://pubmed.ncbi.nlm.nih.gov/40579173/]
• 25. Lineweaver–Burk plot [https://en.wikipedia.org/wiki/Lineweaver%E2%80%93Burk_plot]
• 26. CHE 341 Lab 5 - Tyrosinase Kinetics [https://condor.depaul.edu/jmaresh/341/Lab5/CHE341_5_Kinetics_12.html]
• 27. Comparison of various estimation methods for the ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6989224/]
• 28. 10.2: The Equations of Enzyme Kinetics [https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Physical_Chemistry_for_the_Biosciences_(LibreTexts)/10%3A_Enzyme_Kinetics/10.02%3A_The_Equations_of_Enzyme_Kinetics]
• 29. Mastering Lineweaver-Burk Plots: A Comprehensive Guide ... [https://www.2minutemedicine.com/mastering-lineweaver-burk-plots-a-comprehensive-guide-for-mcat-biochemistry/]
• 30. How to Use Dixon's Plot for Enzyme Inhibition Kinetics [https://www.letstalkacademy.com/dixon-plot-enzyme-inhibition-kinetics-1-over-vi-vs-i/]
• 31. Lineweaver-Burk, Hanes, Eadie-Hofstee and Dixon plots in ... [https://pubmed.ncbi.nlm.nih.gov/6310268/]
• 32. Optimizing enzyme inhibition analysis: precise estimation ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12141731/]
• 33. EVALUATION OF COMPETITIVE INHIBITION USING A ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6952120/]
• 34. A Model-informed Shortcut to Estimate Inhibition Constants [https://www.siam.org/publications/siam-news/articles/a-model-informed-shortcut-to-estimate-inhibition-constants/]
• 35. Estimation of K(i) in a competitive enzyme-inhibition model [https://experts.arizona.edu/en/publications/estimation-of-ki-in-a-competitive-enzyme-inhibition-model-compari]
• 36. Mathbiomed/50-BOA [https://github.com/Mathbiomed/50-BOA]
• 37. On the use of the experimentally determined enzyme ... [https://pubmed.ncbi.nlm.nih.gov/28571743/]
• 38. Monoamine Oxidase Inhibitory Constituents of Propolis [https://www.mdpi.com/1420-3049/19/11/18936]
• 39. Cholinesterase inhibition studies by stopped-flow ... [https://www.sciencedirect.com/science/article/abs/pii/0003269777900264]
• 40. Solution Kinetics Measurements Suggest HIV-1 Protease ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2771923/]
• 41. Fluorogenic Assay for Inhibitors of HIV-1 Protease with Sub ... [https://www.nature.com/articles/srep11286]
• 42. 11. Experimental Enzyme Kinetics; Linear Plots and ... [https://ecampusontario.pressbooks.pub/bioc2580/chapter/experimental-enzyme-kinetics-linear-plots-and-enzyme-inhibition/]
• 43. 6.4: Enzyme Inhibition [https://bio.libretexts.org/Workbench/Biochem_Remix_Acevedo/06%3A_Enzyme_Activity/6.04%3A_Enzyme_Inhibition]
• 44. Enzyme inhibitor [https://en.wikipedia.org/wiki/Enzyme_inhibitor]
• 45. Classification of difference between inhibition constants ... [https://pubmed.ncbi.nlm.nih.gov/22224402/]
• 46. Optimum design of experiments for enzyme inhibition ... [https://pubmed.ncbi.nlm.nih.gov/21442525/]
• 47. precise estimation with a single inhibitor concentration [https://pubmed.ncbi.nlm.nih.gov/40473596/]
• 48. Error structure as a function of substrate and inhibitor ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC1146758/]
• 49. Competition and allostery govern substrate selectivity of ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4603459/]
• 50. Assessment of Enzyme Inhibition: A Review with Examples ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6152246/]
• 51. Probing the modulation of enzyme kinetics by multi- ... [https://www.nature.com/articles/s41467-025-61631-2]
• 52. Multi-Enzyme Synergy and Allosteric Regulation in the ... [https://www.mdpi.com/2073-4344/15/8/718]
• 53. Identification of Inhibitor Concentrations to Efficiently ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2909451/]
• 54. On the use of the experimentally determined enzyme ... [https://www.sciencedirect.com/science/article/pii/S0006291X1731077X]
• 55. Estimating the Product Inhibition Constant from Enzyme ... [https://www.mdpi.com/2073-4344/10/8/853]
• 56. In silico methods for drug-target interaction prediction - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC12570315/]
• 57. Combining Experimental Data and Computational Methods for ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC7594097/]
• 58. Benchmarking compound activity prediction for real-world ... [https://www.nature.com/articles/s42004-024-01204-4]
• 59. Computational Prediction and Experimental Values of ... [https://www.mdpi.com/2079-4991/11/11/2997]
• 60. Measurement of enzyme kinetics and inhibitor constants ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2722910/]
• 61. WelQrate: Defining the Gold Standard in Small Molecule ... [https://arxiv.org/html/2411.09820v1]
• 62. Correlation of Experimental and Calculated Inhibition ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10889394/]
• 63. Clinical pharmacology and pharmacokinetics: questions and ... [https://www.ema.europa.eu/en/human-regulatory-overview/research-development/scientific-guidelines/clinical-pharmacology-pharmacokinetics/clinical-pharmacology-pharmacokinetics-questions-answers]
• 64. Benchmarking ANI potentials as a rescoring function and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10965596/]