Mastering Michaelis-Menten Kinetics with NONMEM: A Comprehensive Guide to Parameter Estimation for Drug Development

Abstract

This article provides a comprehensive guide for researchers and drug development professionals on estimating Michaelis-Menten pharmacokinetic parameters using NONMEM, the industry-standard nonlinear mixed-effects modeling software [citation:7]. It covers the full scope from foundational concepts of saturable elimination to advanced application, troubleshooting model instability [citation:1], and comparative analysis with emerging AI-based methodologies [citation:2]. The content details practical workflows for model implementation, addresses common convergence challenges, explores strategies for generating robust initial estimates [citation:3], and demonstrates application in therapeutic dose optimization [citation:4]. This guide synthesizes traditional best practices with the latest advancements in automated modeling pipelines to equip scientists with the knowledge to reliably characterize nonlinear pharmacokinetics.

Understanding Michaelis-Menten Kinetics and NONMEM's Role in Population PK/PD Analysis

Theoretical Foundations of Michaelis-Menten Kinetics

The Michaelis-Menten equation describes the rate of enzymatic reactions, where the velocity (v) of product formation depends on the substrate concentration ([S]) [1]. The fundamental form of the equation is: v = (Vmax × [S]) / (Km + [S]) [1] [2] [3].

The two critical parameters are:

• V_max (Maximum Reaction Velocity): The theoretical maximum rate of the reaction, achieved when all enzyme active sites are saturated with substrate [1]. In pharmacokinetics, it represents the maximum capacity of an enzyme system to metabolize a drug.
• Km (Michaelis Constant): Defined as the substrate concentration at which the reaction velocity is half of Vmax [1] [2]. It is an inverse measure of the enzyme's affinity for the substrate; a lower K_m indicates higher affinity [4].

The model is derived from the foundational enzymatic mechanism: E + S ⇌ ES → E + P where E is the free enzyme, S is the substrate, ES is the enzyme-substrate complex, and P is the product [1] [3]. The derivation assumes steady-state conditions for the ES complex or rapid equilibrium binding [1] [3].

In pharmacokinetics (PK), this model is adapted to describe nonlinear drug elimination, commonly observed with drugs like phenytoin, voriconazole, and ethanol [5]. Here, the rate of drug metabolism (or elimination) is saturable. The PK analogue of the Michaelis-Menten equation is: -dC/dt = (Vmax × C) / (Km + C) where C is the plasma drug concentration [5] [2].

Pharmacokinetic Translation and Clinical Significance

The translation of in vitro enzyme kinetics to in vivo pharmacokinetics is central to predicting drug behavior. Key derived PK equations include [5]:

• Clearance (CL): At steady state, clearance becomes concentration-dependent: CL = Vmax / (Km + C_ss).
• Dosing Rate (DR): For drugs with nonlinear kinetics, the maintenance dose rate to achieve a target steady-state concentration (Css) is: DR = (Vmax × Css) / (Km + C_ss).

When drug concentration C is much lower than Km (C << Km), the elimination approximates first-order kinetics (linear pharmacokinetics). When C is much greater than Km (C >> Km), the elimination rate approaches the constant V_max, demonstrating zero-order kinetics [1] [5]. This transition underpins the nonlinear, dose-dependent pharmacokinetics critical for drugs with a narrow therapeutic index.

The specificity constant (kcat/Km), representing the enzyme's catalytic efficiency, is crucial for understanding in vivo drug metabolism and interactions [1]. Drugs can act as enzyme inducers (increasing Vmax) or inhibitors (decreasing Vmax or increasing apparent K_m), altering their own kinetics or that of co-administered drugs [5].

Table 1: Representative Drugs Exhibiting Michaelis-Menten Pharmacokinetics

Drug/Therapeutic Area	Primary Metabolizing Enzyme	Clinical PK Implication
Phenytoin (Anticonvulsant)	CYP2C9	Dose-dependent elimination; small dose increases can lead to large rises in concentration [5].
Voriconazole (Antifungal)	CYP2C19	Nonlinear PK; therapeutic drug monitoring required [5].
Ethanol	Alcohol dehydrogenase	Zero-order elimination at high concentrations [5].
Theophylline (Bronchodilator)	CYP1A2	Concentration-dependent clearance; narrow therapeutic window [5].

Parameter Estimation Methods & The Role of NONMEM

Accurate estimation of Vmax and Km from experimental data is paramount. Methods range from traditional linearizations to modern nonlinear mixed-effects modeling.

• Linear Transformation Methods: Historically, plots like Lineweaver-Burk (1/v vs. 1/[S]) and Eadie-Hofstee (v vs. v/[S]) were used to graphically estimate parameters [4]. These methods are simple but can distort error structures and are statistically inferior for parameter estimation [4] [6].
• Direct Nonlinear Regression: Fitting the untransformed velocity vs. concentration data directly to the Michaelis-Menten equation using nonlinear least squares regression is more robust and avoids the biases of linear transformations [4] [6].

In clinical pharmacology, population pharmacokinetic (PopPK) modeling with nonlinear mixed-effects models (NONMEM) is the gold standard for estimating Vmax and Km from sparse clinical data. It distinguishes between:

• Fixed Effects: The typical population values of Vmax and Km.
• Random Effects: Inter-individual variability (IIV) around these parameters and residual unexplained variability [7].

A major challenge in nonlinear modeling is obtaining good initial parameter estimates for the optimization algorithm. Poor initial estimates can lead to model convergence failures [7]. Strategies to generate initial estimates include [7]:

• Adaptive Single-Point Method: Using concentrations from specific time points (e.g., after first dose or at steady-state) with known dosing information to approximate clearance and volume.
• Graphical Methods: Visual inspection of concentration-time profiles.
• Naïve Pooled Data Analysis: Treating all data as if from a single individual for initial approximations.
• Parameter Sweeping: Testing a range of candidate values and selecting those with the best predictive performance [7].

Recent research has focused on developing automated pipelines that integrate these data-driven methods to generate robust initial estimates without user input, facilitating large-scale and automated PopPK analyses [7].

Table 2: Comparison of Parameter Estimation Methods for Michaelis-Menten Kinetics

Method	Principle	Advantages	Disadvantages/Considerations
Lineweaver-Burk Plot	Linear transform: Plot 1/v vs. 1/[S]. Vmax = 1/y-intercept; Km = slope/y-intercept [4].	Simple visualization.	Prone to error propagation; gives undue weight to low-concentration data points; statistically unreliable [4].
Direct Nonlinear Regression (NONMEM)	Fits [S] vs. time data directly to the differential form of the MM equation [4].	Most accurate and precise; handles error structure correctly; suitable for sparse, population data [4].	Requires specialized software; computationally intensive; needs good initial estimates.
Eadie-Hofstee Plot	Linear transform: Plot v vs. v/[S]. Vmax = y-intercept; Km = -slope [4].	Visualizes data spread.	Less distortion than Lineweaver-Burk but still suboptimal vs. nonlinear methods [4].
Automated Pipeline (e.g., R-based)	Combines single-point, graphical, and NCA methods to generate initial estimates for PopPK [7].	Automated, robust, applicable to rich and sparse data; reduces modeler burden [7].	Relatively new approach; may require validation for specific model structures.

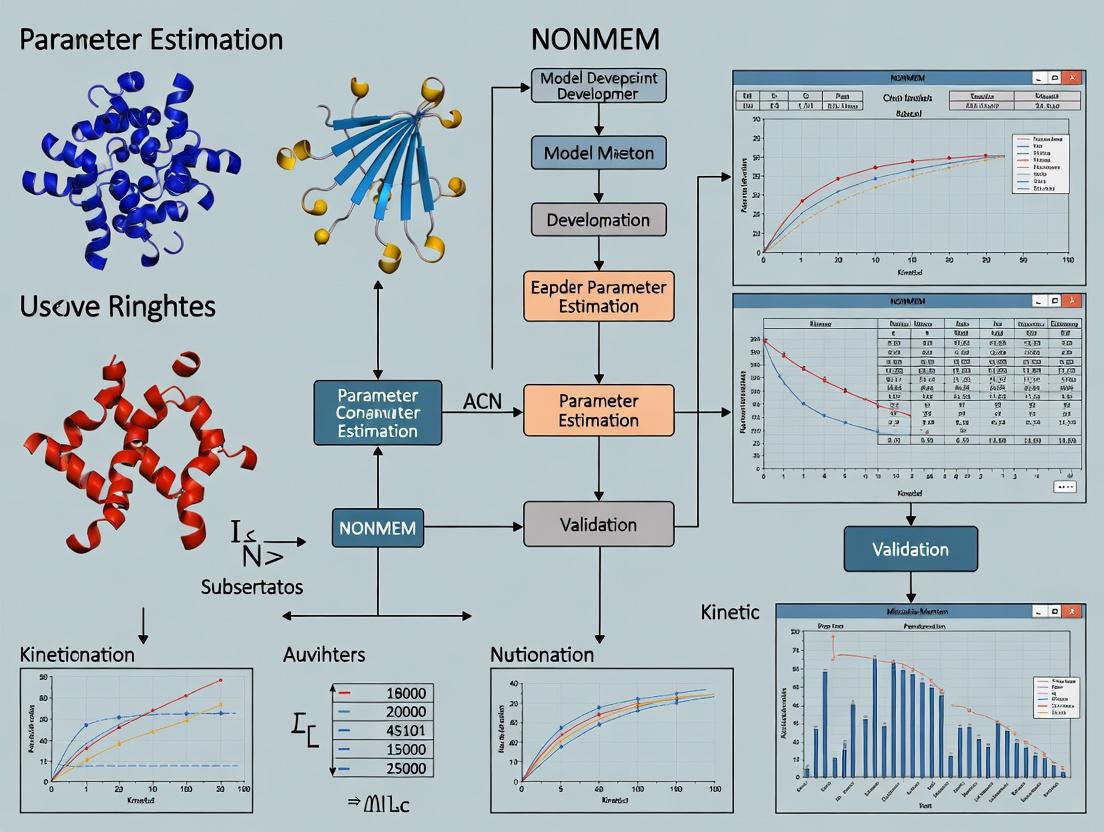
Diagram: Workflow for Michaelis-Menten Parameter Estimation in Pharmacokinetics

Advanced Protocols: NONMEM Implementation for MM Parameters

Protocol 1: Implementing a Basic Michaelis-Menten Elimination Model in NONMEM

This protocol outlines the steps to code a one-compartment model with Michaelis-Menten elimination in a NONMEM control stream ($PROBLEM, $INPUT, etc.).

• $SUBROUTINE: Select ADVAN6 or ADVAN13 for general differential equation solutions, or ADVAN10 for analytical solutions to specific nonlinear models. Define TOL appropriately for stiff equations.
• $MODEL: Define compartments (e.g., DEPOT, CENTRAL).

• $PK:

• $DES (Differential Equations for ADVAN6):

• $ERROR: Define an appropriate residual error model (e.g., additive, proportional, or combined).

• $ESTIMATION: Use a method like FOCE INTERACTION for reliable estimation of nonlinear models with random effects [8].

• $COVARIANCE: Request covariance step to obtain standard errors of parameter estimates.

Protocol 2: Generating Initial Estimates for PopPK Analysis [7]

An automated R-based pipeline can generate initial estimates for THETA:

• Data Preparation: Pool data across individuals based on time after dose (TAD), calculating median concentrations in time bins.
• Estimate Half-life: Perform linear regression on the terminal phase of the pooled log-concentration vs. time data.
• Calculate Parameters:
  • For intravenous data, use an early post-first-dose point (within 0.2 half-lives) to estimate volume: Vd ≈ Dose / C₁.
  • Use steady-state maximum (Css,max) and minimum (Css,min) concentrations to estimate clearance: CL ≈ Dose * ln(Css,max/Css,min) / [τ * (Css,max - Css,min)], where τ is the dosing interval.
  • Approximate V_max and K_m from a range of doses and steady-state concentrations using the linearized form: 1/DR = (Km/Vmax) * (1/Css) + 1/Vmax.
• Parameter Sweeping: If analytical methods are insufficient, simulate concentration-time profiles for a grid of candidate (Vmax, Km) pairs and select the pair minimizing the relative root mean squared error (rRMSE) between observed and predicted data.

The Scientist's Toolkit: Essential Research Reagent Solutions

Table 3: Key Reagents & Software for MM Parameter Estimation Research

Item/Software	Function in MM/PK Research	Example/Note
NONMEM	Industry-standard software for nonlinear mixed-effects modeling of PK/PD data. Used for population estimation of Vmax, Km, and their variability [4] [8].	ICON Development Solutions. Required for implementing protocols in Sections 3 & 4.
R or Python	Open-source programming environments for data simulation, exploratory analysis, running automated estimation pipelines [7], and creating diagnostic plots.	Packages: nlmixr2, mrgsolve (R), PyDarwin, Pharmpy (Python).
ADP-Glo Kinase Assay	A luminescent method to measure kinase activity by quantifying ADP production. Used to generate initial velocity (v) vs. substrate concentration ([S]) data for in vitro enzyme kinetic studies [6].	Example from c-Src kinase inhibition studies [6].
High-Throughput Microplate Reader	Instrument to measure absorbance, fluorescence, or luminescence in 96- or 384-well plates. Essential for rapidly collecting the dense [S]-v data required for robust in vitro MM parameter fitting [6].	GloMax Discover (Promega) [6].
GraphPad Prism	Commercial software for scientific graphing and basic nonlinear regression. Useful for initial exploratory fitting of in vitro MM kinetics and inhibitor IC₅₀/Kᵢ calculations [6].	Commonly used before advanced PopPK analysis in NONMEM.
SigmaPlot/Solver (Excel)	Software for nonlinear curve fitting. Can be used to fit data directly to the MM equation to obtain preliminary Vmax and Km estimates [5] [6].	An accessible tool for direct nonlinear regression [6].

Saturable elimination, also known as zero-order or capacity-limited elimination, is a critical pharmacokinetic (PK) phenomenon where drug clearance pathways become saturated at higher concentrations, leading to non-proportional increases in systemic exposure with dose escalation [9]. This occurs when the enzymes responsible for metabolism (e.g., cytochrome P450 isoforms) or active transport processes reach their maximum catalytic capacity (Vmax) [10]. In contrast, first-order elimination, which governs most drugs at therapeutic doses, describes a process where a constant fraction of drug is eliminated per unit time [9].

The transition from first-order to zero-order kinetics has profound implications for drug safety and efficacy. When elimination is saturated, small increases in dose can lead to disproportionately large increases in drug exposure (area under the curve, AUC), dramatically elevating the risk of toxicity [9]. This is a cornerstone of nonlinear pharmacokinetics and is classically described by the Michaelis-Menten (M-M) equation [10].

Understanding and characterizing saturable elimination is therefore essential across all drug modalities. For small molecules, saturation often involves metabolic enzymes like CYP2C9, CYP2D6, or CYP3A4. For biologics such as monoclonal antibodies, saturation can occur via target-mediated drug disposition (TMDD), where the high-affinity binding to a pharmacological target acts as a saturable elimination pathway [11]. Accurately estimating the parameters of the M-M equation (Vmax and Km) is thus a fundamental task in model-informed drug development (MIDD), enabling the prediction of safe and effective dosing regimens across populations [11].

This application note details the principles, experimental strategies, and advanced analytical methodologies—particularly using NONMEM for parameter estimation—to study saturable elimination throughout the drug development lifecycle.

Quantitative Characterization of Elimination Kinetics

The fundamental difference between linear and saturable elimination is quantitatively distinct, impacting all key pharmacokinetic parameters. The following table contrasts the characteristics of both kinetic processes [12] [9].

Table 1: Characteristics of First-Order vs. Zero-Order (Saturable) Elimination Kinetics

Pharmacokinetic Parameter	First-Order (Linear) Elimination	Zero-Order (Saturable) Elimination
Governing Principle	A constant fraction of drug is eliminated per unit time.	A constant amount of drug is eliminated per unit time.
Rate of Elimination	Proportional to drug concentration (Rate = ke × [C]).	Constant, independent of drug concentration (Rate = Vmax).
Mathematical Description	dC/dt = -ke × C	dC/dt = -Vmax
Plasma Concentration-Time Profile	Exponential decay. Linear on a semi-log plot.	Linear decay.
Half-life (t½)	Constant, independent of dose.	Increases with increasing dose/concentration.
Area Under the Curve (AUC)	Increases proportionally with dose.	Increases more than proportionally with dose.
Time to Eliminate Drug	Independent of dose (~4-5 half-lives).	Dependent on dose; longer with higher doses.
Clinical Dose Predictability	Highly predictable; doubling dose doubles exposure.	Unpredictable; small dose increases can cause large exposure spikes.
Common Examples	Most drugs at therapeutic doses (e.g., amoxicillin, lorazepam).	Phenytoin, salicylates (high dose), ethanol, paclitaxel [9].

The Michaelis-Menten equation bridges these concepts, describing the velocity (V) of an enzymatic reaction or saturable process as a function of substrate concentration ([S]) [10]: V = (Vmax × [S]) / (Km + [S]) Where:

• Vmax is the maximum elimination rate (capacity).
• Km (Michaelis constant) is the substrate concentration at half of Vmax, representing the affinity of the enzyme/transporter for the substrate.

At very low concentrations ([S] << Km), the equation simplifies to V ≈ (Vmax/Km) × [S], exhibiting first-order kinetics. At high concentrations ([S] >> Km), V ≈ Vmax, and elimination becomes zero-order and saturable [10] [9].

Protocols for Characterizing Saturable Elimination

Protocol for In Vitro Michaelis-Menten Parameter Estimation Using NONMEM

Adapted from the simulation study by Cho & Lim (2018) [10] [13].

Objective: To determine the most accurate and precise method for estimating Vmax and Km from in vitro enzyme kinetic data, comparing traditional linearization methods with nonlinear estimation in NONMEM.

Materials & Software:

• R Statistical Software (with deSolve package)
• NONMEM (Version 7.3 or higher)
• Simulated or experimental time-course substrate concentration data.

Procedure:

• Data Generation/Collection:

  • For simulation studies: Generate substrate depletion time-course data for multiple initial substrate concentrations (e.g., 20.8, 41.6, 83, 166.7, 333 mM) using the M-M differential equation: d[S]/dt = - (Vmax × [S]) / (Km + [S]). Incorporate realistic residual error models (additive, proportional, or combined) [10].
  • For experimental data: Conduct in vitro metabolic stability assays with human liver microsomes or recombinant enzymes, measuring substrate loss over time at 5-6 different starting concentrations.

• Data Preparation for Different Estimation Methods:

  • NM (NONMEM Nonlinear): Use the raw [S]-time data directly.
  • LB (Lineweaver-Burk) & EH (Eadie-Hofstee): Calculate initial velocity (Vi) for each concentration from the linear slope of the early time points. Transform data: LB uses 1/Vi vs. 1/[S]; EH uses Vi vs. Vi/[S] [13].
  • NL (Nonlinear Vi-[S]): Use the calculated Vi and corresponding [S] pair.
  • ND (Nonlinear Delta): Calculate the average rate between adjacent time points (VND) and the midpoint concentration ([S]ND) [13].

• Parameter Estimation in NONMEM:

  • Code the appropriate structural model for each method in NONMEM control files.
  • For method NM, implement the differential equation directly.
  • For methods LB and EH, use linear models on the transformed data. For NL and ND, use the M-M algebraic equation.
  • Use the First-Order Conditional Estimation (FOCE) method with interaction.
  • Perform estimation for all datasets (simulated replicates or experimental runs).

• Analysis & Comparison:

  • For each method, compile the estimated Vmax and Km values.
  • Calculate measures of accuracy (e.g., median relative error) and precision (e.g., 90% confidence interval width) relative to the known true values (simulation) or the most robust estimate.
  • Expected Outcome: As demonstrated by Cho & Lim, nonlinear regression fitting the full [S]-time data (NM method) typically provides the most accurate and precise parameter estimates, especially with complex error structures, outperforming traditional linearization methods (LB, EH) [10].

Protocol for Identifying Saturable Elimination in Phase I Clinical Data Using Machine Learning

Informed by Certara's application of machine learning for PK/PD modeling [14].

Objective: To efficiently identify the structural PK model—including the potential for saturable (Michaelis-Menten) elimination—that best describes complex Phase I clinical trial data.

Materials & Software:

• Phase I rich concentration-time data.
• Machine learning-enabled pharmacometric software (e.g., containing genetic algorithm capabilities).
• Standard NONMEM/Pirana for final model refinement.

Procedure:

• Exploratory Data Analysis (EDA):

  • Plot individual patient concentration-time profiles.
  • Plot AUC vs. Dose. A greater-than-proportional increase suggests saturable elimination or absorption [15].
  • Plot clearance (CL) vs. concentration. A decreasing trend with higher concentrations suggests saturable elimination.

• Define the Model Space:

  • Define a set of plausible structural models to be tested. This is a critical step driven by the scientist.
  • Absorption: First-order with/without lag time, sequential zero-first order, distributed delay function.
  • Distribution: 1-, 2-, or 3-compartment models.
  • Elimination: Linear (first-order) clearance vs. Michaelis-Menten (saturable) clearance.
  • Covariates: Include potential relationships (e.g., weight on volume, age on clearance).

• Machine Learning Model Search:

  • Configure a genetic algorithm or other global search algorithm to explore the defined model space.
  • The algorithm will automatically run hundreds to thousands of model configurations, evaluating each based on a fitness score (e.g., objective function value penalized for number of parameters) [14].
  • The search is non-sequential, evaluating combinations of features (e.g., dual-compartment with saturable elimination) that might be missed in manual stepwise building.

• Model Evaluation and Selection:

  • Review the top-performing models identified by the ML algorithm.
  • Perform standard pharmacometric diagnostics on the leading candidates: goodness-of-fit plots, visual predictive checks, precision of parameter estimates.
  • Final Selection: The scientist makes the final decision based on statistical fit, parsimony, and biological plausibility. The ML tool provides robust, data-driven candidates [14].

Diagram 1: Workflow for Identifying Saturable Kinetics in Clinical Data

The Scientist's Toolkit: Essential Reagents & Software

Table 2: Key Research Reagent Solutions for Studying Saturable Elimination

Tool/Reagent Category	Specific Examples	Function in Saturable Elimination Research
In Vitro Metabolism Systems	Human liver microsomes (HLM), recombinant CYP enzymes, hepatocytes.	Provide the biological enzymes to conduct in vitro kinetic studies for estimating initial Vmax and Km values for small molecules.
Transport Assay Systems	Transfected cell lines (e.g., MDCK, HEK293) overexpressing specific transporters (OATP1B1, P-gp).	Characterize saturable active transport processes that may contribute to uptake or elimination.
Target Proteins (for Biologics)	Soluble recombinant target antigens, cell lines expressing membrane-bound targets.	Essential for characterizing the target-binding affinity (KD) and capacity (Rmax) in TMDD assays, a key saturable pathway for biologics.
Simulation & Modeling Software	R (with deSolve, nlmixr), NONMEM, Monolix, Phoenix NLME.	The primary platform for nonlinear mixed-effects modeling, enabling population estimation of M-M parameters from clinical data.
Global Optimization Algorithms	Particle Swarm Optimization (PSO), Genetic Algorithms (GA).	Address challenges in nonlinear model fitting, such as parameter identifiability and convergence, by searching the global parameter space [16].
Specialized NONMEM Extensions	P-NONMEM [16], Fractional Differential Equation (FDE) subroutines [17].	Extend NONMEM's capability for complex models: PSO integration for robust estimation [16]; FDEs for modeling anomalous "power-law" kinetics sometimes linked to nonlinear elimination [17].
Machine Learning Platforms for MIDD	Certara's ML tools, custom Python/R scripts using TensorFlow/Scikit-learn.	Automate the exploration of complex PK model spaces to efficiently identify the inclusion of saturable elimination mechanisms [14].

Advanced Analytical Considerations & NONMEM Workflow

Addressing Parameter Identifiability in Nonlinear Models

A major challenge in estimating M-M parameters (Vmax, Km) from in vivo data is statistical non-identifiability, where multiple parameter combinations yield an equally good fit to the data [16]. This often leads to estimation failures or unstable results in NONMEM.

Protocol Mitigation Strategies:

• Informative Prior Design: Collect rich data across a wide dose range, especially with doses designed to produce concentrations near and above the estimated Km.
• Use of Global Optimizers: Implement hybrid algorithms like LPSO (Particle Swarm Optimization coupled with local search) within or alongside NONMEM. As derivative-free methods, they are less prone to failure from singularity issues and can better navigate complex objective function landscapes to find global solutions [16].
• Model Simplification: If Vmax and Km are not jointly identifiable, consider fixing one parameter to a literature value from in vitro studies (e.g., Km) and estimating the other (Vmax in vivo).

NONMEM Workflow for Population M-M Parameter Estimation

Diagram 2: NONMEM Workflow for Population Michaelis-Menten Analysis

Application Across Modalities: Small Molecules vs. Biologics

The manifestation and analysis of saturable elimination differ between drug classes:

• Small Molecules: Saturable elimination is primarily metabolism-driven. The focus is on characterizing the specific enzymes involved (e.g., via chemical inhibition assays in vitro) and applying the standard M-M framework. Phenytoin and high-dose aspirin are classic examples [9]. The NONMEM model typically adds a Michaelis-Menten clearance term: CL = (Vmax / (Km + C)).

• Biologics (e.g., mAbs): Saturable elimination is often target-mediated (TMDD). At low doses, the drug binds with high affinity to its target, and the drug-target complex is internalized and degraded, creating a high-capacity, saturable elimination pathway. At higher doses, the target is saturated, and linear, non-specific clearance pathways dominate [11]. Modeling is more complex, often requiring a quasi-equilibrium or quasi-steady-state approximation of the full TMDD model within NONMEM, which still relies on estimating a saturation constant (Km) related to target affinity and turnover.

In both cases, the accurate estimation of saturation parameters is critical for first-in-human dose prediction, optimizing dosing regimens for Phase II/III, and predicting drug-drug interaction potential (for small molecules) [11].

NONMEM (Nonlinear Mixed Effects Model) is a computer program written in FORTRAN 90/95, designed for fitting general nonlinear regression models to data, with specialized application in population pharmacokinetics (PK) and pharmacodynamics (PD) [18] [19]. Developed by Lewis Sheiner and Stuart Beal at the University of California, San Francisco, it has become the industry-standard software for population PK/PD analysis for over 30 years [20] [21]. The software is particularly powerful for analyzing data with sparse sampling or variable designs across individuals, as it accounts for both inter-individual (random effects) and intra-individual variability, as well as measured covariates (fixed effects) [18] [19].

The NONMEM system comprises three core components [20] [18]:

• NONMEM: The foundational, general nonlinear regression program.
• PREDPP (PRED for Population Pharmacokinetics): A specialized subroutine library that handles standard and complex kinetic models, freeing users from coding common differential equations. It includes a suite of ADVAN model subroutines [19].
• NM-TRAN (NONMEM Translator): A preprocessor that translates user-friendly control streams and data files into the formats required by NONMEM [20] [18].

The current version, NONMEM 7.6, includes advanced estimation methods such as Stochastic Approximation Expectation-Maximization (SAEM) and Markov-Chain Monte Carlo Bayesian Analysis (BAYES, NUTS), along with support for complex mathematical constructs like delay differential equations (ADVAN16, ADVAN17) and distributed delay convolutions [20]. It also supports parallel computing to reduce run times for large problems [20].

The following diagram illustrates the workflow and relationship between these core components and the user's inputs.

NONMEM System Architecture and Workflow

Core Components and Model Library

NONMEM's power for pharmacometric analysis is largely enabled by the PREDPP library. Users select a pre-defined model type via ADVAN subroutines in their control stream. For research focused on Michaelis-Menten kinetics, ADVAN10 is directly applicable as it implements a one-compartment model with Michaelis-Menten elimination [19]. Other ADVAN subroutines support a wide range of linear and nonlinear PK/PD models.

Table: Selected PREDPP (ADVAN) Model Subroutines [19]

Model Subroutine	Compartments	Basic Parameters	Model Description
ADVAN1	1 Central, 1 Output	K, V	One-compartment linear model.
ADVAN2	1 Depot, 1 Central, 1 Output	KA, K, V	One-compartment model with first-order absorption.
ADVAN3	1 Central, 1 Peripheral, 1 Output	K, K12, K21	Two-compartment linear mammillary model.
ADVAN4	1 Depot, 1 Central, 1 Peripheral, 1 Output	KA, K, K23, K32	Two-compartment model with first-order absorption.
ADVAN10	1 Central, 1 Output	VM, KM	One-compartment model with Michaelis-Menten elimination.
ADVAN13	General Nonlinear	User-defined	General nonlinear model with stiff/non-stiff ODE solver (LSODA).

The Scientist's Toolkit: Essential Research Reagents and Materials

For conducting NONMEM-based Michaelis-Menten research, the following components are essential.

Table: Essential Toolkit for NONMEM-based Research

Item	Function / Description	Key Considerations
NONMEM Software	The core estimation engine for performing nonlinear mixed-effects modeling [20].	Licensed annually from ICON plc. Version 7.6 is the latest [20].
Fortran Compiler	Required to compile NONMEM's source code into an executable program [20] [22].	Intel Fortran Compiler 9.0+ or gFortran for Windows/Linux are common [20].
Control Stream File (.ctl)	A user-written text file containing all modeling instructions, commands, and model code for NM-TRAN [19] [22].	Defines the structural model ($SUB, $PK), error model ($ERROR), estimation method ($EST), and requested output ($TABLE).
Data File (.csv or .prn)	A text file containing the experimental or clinical data for analysis [19] [22].	Must include required data items (e.g., ID, TIME, DV, AMT) in a space- or comma-delimited format.
Interface/Manager	Third-party tools that facilitate project management, run execution, and graphical diagnostics [19].	Examples include Pirana, Wings for NONMEM (WFN), and Perl Speaks NONMEM (PsN).
Graphical Diagnostic Tool	Software for generating diagnostic plots (e.g., goodness-of-fit, VPC) from NONMEM output tables [23].	R (with packages like xpose), Xpose, or custom scripts in Python/MATLAB.

Application to Michaelis-Menten Parameter Estimation

The Michaelis-Menten equation (V = (Vmax * [S]) / (Km + [S])) is fundamental for characterizing enzyme kinetics and saturable elimination processes in drug metabolism [24]. Accurate estimation of its parameters, the maximum reaction rate (Vmax) and the Michaelis constant (Km), is critical for in vitro to in vivo extrapolation and predicting nonlinear PK.

Traditional linearization methods (e.g., Lineweaver-Burk, Eadie-Hofstee) are prone to statistical bias because they distort the error structure of the data. Nonlinear mixed-effects modeling with NONMEM provides a more robust framework by directly fitting the nonlinear model to the data, properly handling both fixed effects (typical parameter values) and random effects (inter-experiment/inter-individual variability) [24].

Comparative Performance of Estimation Methods

A key simulation study directly compared the performance of various estimation methods for Michaelis-Menten parameters [24]. The results unequivocally support the use of nonlinear methods in NONMEM.

Table: Performance Comparison of Michaelis-Menten Parameter Estimation Methods [24]

Estimation Method	Category	Relative Accuracy & Precision for Vmax and Km	Key Finding
Nonlinear Method (NM) in NONMEM	Nonlinear, Mixed-Effects	Most accurate and precise	Provides the most reliable parameter estimates by correctly specifying the error model.
Traditional Linearization Methods (e.g., Lineweaver-Burk)	Linear, Transform-based	Less accurate and precise	Amplifies error and distorts variance, leading to biased parameter estimates.
Iterative Two-Stage (ITS)	Hybrid, Nonlinear	Intermediate performance	More robust than linearization but generally less efficient than full population methods like FOCE or SAEM.

The study found that the superiority of NONMEM's nonlinear estimation was particularly evident when data followed a combined (proportional plus additive) error model, which is common in real-world biological data [24]. This makes NONMEM the preferred tool for reliable Michaelis-Menten parameter estimation in pharmacological research.

Experimental Protocols for Michaelis-Menten Analysis

This section provides detailed, actionable protocols for setting up and executing a NONMEM analysis aimed at estimating Michaelis-Menten parameters, as informed by simulation studies and tutorial guides [24] [23].

Protocol 1: Simulation-Based Validation of Method Performance

Objective: To validate and compare the accuracy of different estimation methods for Vmax and Km using simulated in vitro elimination kinetic data [24].

• Define True Parameters & Model:

  • Set population values for Vmax (e.g., 100 nmol/min/mg) and Km (e.g., 10 µM).
  • Define an error model: combined additive (σ_add) and proportional (σ_prop) error is recommended (e.g., DV = IPRED * (1 + ε₁) + ε₂, where ε₁ and ε₂ are normally distributed with mean 0 and variances σ_prop² and σ_add²).

• Generate Simulation Dataset:

  • Using software like R, generate substrate concentrations ([S]) over a range (e.g., 0.2Km to 5Km).
  • For each [S], calculate the true reaction velocity (V) using the Michaelis-Menten equation.
  • Add random noise to V based on the defined error model to create observed values (DV).
  • Replicate this process to create N (e.g., 1000) simulated datasets [24].

• Prepare NONMEM Data File:

  • Structure a .csv file with columns: SIM, ID, TIME, DV, CONC. Use TIME as a placeholder if not time-course data; CONC holds the substrate concentration ([S]).

• Develop NONMEM Control Stream:

  • Use $SUBROUTINE ADVAN10 TOL=6 for Michaelis-Menten kinetics.
  • In $PK: Define VM = THETA(1) * EXP(ETA(1)) and KM = THETA(2) * EXP(ETA(2)). Set initial THETA values close to the true simulated values.
  • In $ERROR: Define IPRED using the Michaelis-Menten equation with model parameters, and define Y = IPRED + IPRED*EPS(1) + EPS(2) for a combined error model.
  • Use an estimation method like FOCE with INTERACTION in $ESTIMATION.

• Execute and Analyze:

  • Run NONMEM for each simulated dataset or use the $SIMULATION functionality.
  • For each run, record the estimated Vmax and Km.
  • Calculate performance metrics (e.g., relative bias, precision) across all simulations to compare with other methods [24].

Protocol 2: Population Analysis of Enzyme Kinetic Data

Objective: To estimate typical population values and inter-assay variability of Vmax and Km from a real in vitro experiment conducted with multiple enzyme preparations (e.g., different hepatocyte lots) [23].

• Data Assembly and Exploration:

  • Compile data from all experiments. Essential data items: ID (experiment/lot number), substrate concentration (CONC or SS as a steady-state indicator), and observed reaction velocity (DV).
  • Perform exploratory graphical analysis (velocity vs. concentration) to check for saturable kinetics and outliers.

• Create NONMEM Data File:

  • Format data as a space- or comma-delimited text file. Map columns using $INPUT in the control stream (e.g., $INPUT ID TIME DV CONC AMT). Use AMT=0 for observation records.

• Base Model Development:

  • Control Stream Setup:
    • $PROBLEM Population Michaelis-Menten Kinetics
    • $DATA your_data.csv IGNORE=@
    • $SUBROUTINE ADVAN10 TOL=6
    • $ABBR (Optional, for advanced reparameterization)
  • Parameter Definition ($PK):
    • Define typical population parameters: TVVM = THETA(1) and TVKM = THETA(2).
    • Define inter-individual variability (IIV) using exponential error models: VM = TVVM * EXP(ETA(1)) and KM = TVKM * EXP(ETA(2)).
    • Initial THETA estimates can come from prior literature or graphical estimates.
  • Error Model ($ERROR):
    • Define the individual prediction: IPRED = (VM * CONC) / (KM + CONC).
    • Choose a residual error model. A proportional error is often suitable: Y = IPRED + IPRED*EPS(1).
  • Estimation and Output:
    • $ESTIMATION METHOD=FOCE INTERACTION MAXEVAL=9999 SIGDIGITS=3
    • $TABLE ID TIME IPRED PRED RES WRES CWRES NOPRINT ONEHEADER FILE=sdtab1
    • $TABLE ID ETA1 ETA2 NOPRINT ONEHEADER FILE=patab1

• Model Evaluation:

  • Run the model and assess convergence (successful covariance step).
  • Generate diagnostic plots (e.g., PRED vs. DV, CWRES vs. PRED) using the output tables to evaluate goodness-of-fit [23].

• Covariate Model Building (Optional):

  • If experiment metadata is available (e.g., protein content, donor age), test for covariate relationships on Vmax or Km in the $PK block using linear or power functions (e.g., TVVM = THETA(1) * (PROT/MEANPROT)THETA(3)).
  • Use objective function value (OFV) changes and diagnostic plots to guide model selection.

The logical process for developing and refining a population Michaelis-Menten model is summarized in the diagram below.

Population Michaelis-Menten Model Development Workflow

Advanced Features and Future Directions

NONMEM 7.6 includes sophisticated features that extend its utility beyond standard PK/PD modeling, several of which are relevant for complex kinetic analyses [20] [25].

• Delay Differential Equations (DDEs): Modeled via ADVAN16 and ADVAN17, these are essential for capturing physiological delays (e.g., in cell proliferation or indirect response models) [20] [25].
• Nonparametric and Bayesian Methods: The software supports nonparametric estimation of parameter distributions, which is valuable when random effects are non-normal [26]. Bayesian analysis (BAYES and NUTS sampling) allows for formal incorporation of prior knowledge [20].
• Cutting-Edge Research: Recent extensions demonstrate NONMEM's adaptability, such as the implementation of fractional differential equation (FDE) models to describe anomalous kinetics or power-law behavior, which can offer more parsimonious models for complex data [17].

NONMEM remains the definitive software for nonlinear mixed-effects modeling in drug development and basic pharmacological research. Its rigorous framework for population parameter estimation, exemplified by its superior performance in estimating Michaelis-Menten constants compared to linearization methods, provides scientists with reliable and interpretable results [24]. The structured protocols for simulation and analysis, combined with its advanced capabilities for handling complex biological processes, ensure that NONMEM will continue to be an indispensable tool for quantifying and predicting nonlinear kinetics in therapeutic research.

Abstract Integrating Michaelis-Menten (MM) kinetics into a Nonlinear Mixed Effects (NLME) modeling framework is essential for accurately characterizing the saturable, non-linear elimination of numerous drugs. This integration involves defining a structural pharmacokinetic (PK) model with MM parameters (Vmax, Km), distinguishing population-level fixed effects from inter-individual random effects, and quantifying residual unexplained variability. Within software like NONMEM, this allows for the analysis of sparse, real-world clinical data to estimate typical population parameters, identify influential covariates, and quantify variability, thereby informing optimized dosing strategies. This application note provides detailed protocols and methodologies for the successful implementation and evaluation of population PK models incorporating MM elimination, framed within a broader thesis on advanced parameter estimation using NONMEM.

1. Introduction: Thesis Context and Rationale This work is situated within a broader thesis investigating robust methodologies for parameter estimation in NONMEM, with a focus on complex, non-linear kinetics. Michaelis-Menten elimination is a fundamental non-linear process where the elimination rate approaches a maximum velocity (Vmax) as concentration increases, with Km representing the concentration at half Vmax. In population modeling, the goal is to estimate the typical values (fixed effects) of Vmax and Km for a population, understand how they vary between individuals (random effects), and account for residual error [27]. This is formally executed within an NLME framework, which simultaneously analyzes data from all individuals, making it uniquely powerful for sparse clinical data [28]. Accurately defining and diagnosing these components—fixed effects, random effects (hierarchically modeled as inter-individual, inter-occasion), and residual error—is critical for developing a model that is both biologically plausible and statistically sound, ultimately supporting drug development decisions from first-in-human studies through to personalized dosing [28] [29].

2. Foundational Components of the NLME-MM Framework A population PK model integrating MM kinetics is composed of interconnected structural, statistical, and covariate sub-models.

• 2.1. Structural (PK) Model: The core kinetic model describes the typical concentration-time profile. For a one-compartment model with intravenous bolus administration and MM elimination, the differential equation is: dA/dt = - (Vmax * C) / (Km + C), where A is amount and C is concentration (C = A/V). Vmax and Km are the key structural parameters to be estimated [30] [31].
• 2.2. Statistical Model: This defines the variability components.
  • Fixed Effects (θ): The typical population values for parameters (e.g., TVVmax, TVKm).
  • Random Effects:
    • Inter-individual Variability (IIV): Modeled using a log-normal distribution to ensure positivity. For example, Vmaxᵢ = TVVmax * exp(ηᵢ_Vmax), where ηᵢVmax is a random variable from a normal distribution with mean 0 and variance ω²Vmax [27] [30].
    • Inter-occasion Variability (IOV): Accounts for variability within an individual across different dosing occasions [32].
    • Residual Unexplained Variability (RUV): Discrepancy between individual model predictions and observed concentrations. Common models include additive (Cobs = Cpred + ε), proportional (Cobs = Cpred * (1 + ε)), or combined error structures [27].
• 2.3. Covariate Model: Explains IIV by relating parameters to patient characteristics (e.g., weight, genotype, renal function). A covariate relationship on Vmax, for instance, can be linear (TVVmax = θ₁ + θ₂*(WT/70)) or allometric (TVVmax = θ₁ * (WT/70)^θ₂) [30]. The inclusion of the ALDH2 genotype on volume of distribution in an alcohol PK model is a specific example of a genetic covariate [31].

3. Protocol: Implementing a Population MM Model in NONMEM

• 3.1. Data Assembly and Preparation
  • Dataset Structure: Prepare a NONMEM-compliant dataset with required columns: ID, TIME, AMT, DV (dependent variable, e.g., concentration), CMT (compartment number), EVID (event identifier), and covariates (e.g., WT, AGE, GENO). Ensure accurate handling of dosing records and observations [33].
  • Data Quality: Perform graphical exploratory data analysis. Identify and document records below the limit of quantification (BLQ). Modern methods (e.g., M3 method) that incorporate the likelihood of BLQ observations are preferred over simple imputation (e.g., LLOQ/2) [27] [32].
• 3.2. Model Development and Estimation Strategy
  • Base Model Building:
    • Start with a structural PK model (e.g., 1- or 2-compartment) with linear elimination to establish a baseline.
    • Introduce MM elimination in place of linear clearance. This often requires switching to an ADVAN13 (general differential equation) subroutine in NONMEM unless a built-in MM option is available.
    • Add IIV to key parameters (typically on Vmax and Km). Use an exponential error model. Estimate the OMEGA variance-covariance matrix.
    • Test different residual error models (additive, proportional, combined).
  • Parameter Estimation: Choose an appropriate estimation method. The First Order Conditional Estimation with interaction (FOCEI) is often a robust starting point. For complex MM models or datasets with high IIV/RUV, more advanced methods like Stochastic Approximation Expectation Maximization (SAEM) or Importance Sampling (IMP) may be required for stability and accuracy [32]. Bayesian Markov Chain Monte Carlo (MCMC) methods are also applicable, especially with informative priors [31].
  • Covariate Analysis:
    • Stepwise Forward Inclusion: Test plausible covariate-parameter relationships (e.g., weight on Vmax, creatinine clearance on Km) using likelihood ratio tests (LRT). A drop in objective function value (OFV) > 3.84 (χ², p<0.05, 1 d.f.) suggests significance.
    • Backward Elimination: Refine the full model by removing non-significant covariates (increase in OFV < 6.63, p<0.01, 1 d.f.) to develop a final parsimonious model [27].
• 3.3. Model Evaluation and Validation
  • Goodness-of-Fit (GOF): Assess basic GOF plots: Observations (DV) vs. Population Predictions (PRED), DV vs. Individual Predictions (IPRED), and Conditional Weighted Residuals (CWRES) vs. TIME or PRED [32].
  • Visual Predictive Check (VPC): The gold standard for model evaluation. Simulate 1000 datasets using the final model parameter estimates and overlay the observed data percentiles with the simulated prediction intervals. This assesses the model's predictive performance across the entire concentration-time profile [17].
  • Numerical Predictive Check (NPC): Provides a quantitative summary of the VPC.
  • Bootstrap: Perform a non-parametric bootstrap (e.g., 1000 samples) to assess the robustness and precision of the final parameter estimates and generate confidence intervals.

4. Data Presentation: Key Parameter Estimates and Model Diagnostics Table 1: Comparison of NONMEM Estimation Methods for NLME-MM Models

Estimation Method	Key Principle	Advantages	Disadvantages	Suitability for MM Models
FO (First Order)	Linearizes the random effects model.	Fast, stable.	Can produce biased estimates with high IIV or RUV.	Poor; not recommended for final MM models.
FOCE/I	Conditional estimation; linearizes residual error.	Generally robust, accurate for many problems.	May struggle with highly non-linear models or sparse data.	Good standard choice.
SAEM	Stochastic sampling of the random effects space.	Accurate for complex, highly non-linear models.	Computationally intensive, results have stochastic variability.	Very good for complex MM models.
Bayesian (MCMC)	Uses prior distributions combined with data likelihood.	Incorporates prior knowledge; useful for sparse data.	Choice of priors influences results; computationally intensive.	Excellent when informative priors exist (e.g., from in vitro Vmax/Km) [32] [31].

Table 2: Example Covariate Relationships in a Structural Parameter Model

Parameter (P)	Covariate Model Form	NONMEM Code Snippet (Example)	Biological Interpretation
Vmax	Allometric scaling by weight	TVVMAX = THETA(1) * (WT/70)THETA(2)	Metabolic capacity scales with body size.
Km	Linear influence of age	TVKM = THETA(3) + THETA(4)*(AGE-40)	Affinity of the enzyme may change with age.
Vd	Influence of genotype (indicator variable)	TVV = THETA(5) * (1 + THETA(6)*GENO)	GENO=1 for variant allele, affecting distribution [31].

Table 3: Example Final Parameter Estimates from a Population MM Analysis (Hypothetical Data)

Parameter	Description	Population Estimate (RSE%)	Inter-Individual Variability (%CV)
TVVmax (mg/h)	Typical max elimination rate	10.5 (5)	30%
TVKm (mg/L)	Typical Michaelis constant	2.1 (12)	45%
TVV (L)	Typical volume of distribution	35.0 (4)	25%
θₐₗₗₒₘ	Allometric exponent on Vmax	0.75 (Fixed)	-
Prop. Err (%)	Proportional residual error	15 (10)	-

5. Experimental Protocol: Case Study on Alcohol PK with MM Elimination

• 5.1. Aim: To develop a population PK model for alcohol incorporating Michaelis-Menten elimination and to identify significant covariates (e.g., body weight, ALDH2 genotype) [31].
• 5.2. Background: Alcohol exhibits capacity-limited metabolism via alcohol dehydrogenase. Data from 34 healthy Japanese subjects with sparse sampling times were available.
• 5.3. Experimental Methodology:
  • Data: Collected blood alcohol concentration-time data after controlled administration. Covariates included demographic data and ALDH2 genotype.
  • Software: Analysis performed using NONMEM 7.3 with MCMC Bayesian estimation.
  • Model Building: a. Structural Model: A one-compartment model with zero-order input (absorption) and Michaelis-Menten elimination was selected. b. Statistical Model: IIV was added to Vmax, Km, and Vd using exponential models. An informative prior distribution for Km was incorporated from an external study to stabilize estimation due to limited data in the later elimination phase. c. Covariate Model: Covariates (weight, age, genotype) were tested on all parameters using a Bayesian framework, evaluating changes in posterior distributions.
  • Model Evaluation: Conducted via posterior predictive checks and examination of Bayesian diagnostics (e.g., trace plots for convergence).
• 5.4. Key Findings: The final model estimated a typical Vd of 49.3 L. A significant covariate effect was found, with ALDH21/2 genotype associated with a 20.4 L lower Vd compared to the ALDH21/1 genotype. The use of Bayesian priors allowed for stable parameter estimation despite data limitations [31].

6. Visualizing the Framework and Workflow

Diagram 1: Workflow for Developing a Population PK Model with MM Kinetics.

Diagram 2: Hierarchical Relationship in an NLME-MM Model.

7. The Scientist's Toolkit: Essential Resources for NLME-MM Analysis Table 4: Key Research Reagent Solutions for Population MM Modeling

Tool/Resource	Function/Purpose	Example/Notes
NONMEM Software	Industry-standard software for NLME modeling. Implements estimation algorithms (FO, FOCE, SAEM, MCMC).	Required for executing the modeling protocols described herein [32] [29].
PDx-Pop / Pirana	Interface and workflow manager for NONMEM. Facilitates model run management, covariate screening, and basic graphics.	Greatly improves efficiency and reproducibility of modeling projects.
R / RStudio with Packages	Statistical computing environment for data preparation, advanced graphics (ggplot2), model diagnostics (xpose), and simulation.	Essential for creating VPCs, custom GOF plots, and conducting bootstraps [17].
Perl Speaks NONMEM (PsN)	Perl-based toolkit for NONMEM. Automates key tasks like VPC, bootstrap, and stepwise covariate modeling (SCM).	Critical for robust model evaluation and automated workflows.
High-Performance Computing (HPC) Cluster	Parallel processing resource.	Significantly reduces runtime for intensive methods like SAEM, IMP, or large bootstraps.
Curated PK/PD Dataset	Clean, well-structured dataset compliant with NONMEM format.	Must include accurate dosing records, concentration data, and covariates. The foundation of any analysis [27] [33].
In Vitro Enzyme Kinetic Data	Prior estimates of Vmax and Km from preclinical studies.	Can be used to inform Bayesian prior distributions in clinical model development, stabilizing estimation [31].

This document details the essential prerequisites and methodologies for conducting robust Michaelis-Menten (MM) pharmacokinetic analysis using the NONlinear Mixed Effects Modeling (NONMEM) software. Within the broader thesis investigating advanced parameter estimation for saturable elimination processes, this guide provides the foundational application notes and protocols. Accurate estimation of Vmax (maximum elimination rate) and Km (substrate concentration at half Vmax) is critical for predicting nonlinear pharmacokinetics, informing dosing regimens, and understanding drug-drug interactions [10]. NONMEM, the industry-standard tool for population analysis, is particularly suited for this task as it employs nonlinear mixed-effects modeling to simultaneously analyze sparse or heterogeneous data from all individuals, providing superior accuracy and precision compared to traditional linearization methods [19] [10].

Prerequisites: Data Structure and Software Environment

Successful MM analysis in NONMEM requires correctly formatted data and an appropriate software ecosystem.

2.1 Data File Structure and Requirements The data file is a comma- or space-delimited text file where each row represents a record (dosing or observation) for an individual [19]. For MM analysis, specific data items are mandatory. The core structure is outlined below:

Table 1: Essential Data Items for NONMEM Analysis using PREDPP

DATA ITEM	DESCRIPTION	REQUIREMENT for MM Analysis	EXAMPLE
ID	Unique subject identifier	Mandatory	1, 2, 3
TIME	Elapsed time since start of analysis	Mandatory	0, 2.5, 5.0
AMT	Dose amount (for dosing records)	Mandatory for dosing events	1000, 0
CMT	Compartment number	Required if using ADVAN subroutines	1, 2
EVID	Event identifier (0=obs., 1=dose, etc.)	Mandatory	0, 1, 4
DV	Dependent variable (observed concentration)	Mandatory for observation records	45.2, 12.7
MDV	Missing dependent variable indicator	Recommended (1=missing, 0=present)	0, 1
RATE	Infusion rate (if applicable)	Optional for zero-order inputs	-2 (for modeled rate)

For a typical single-compartment model with Michaelis-Menten elimination (ADVAN10), the central compartment is designated as CMT=1 and the output compartment as CMT=2 [19]. Accurate EVID and MDV coding is crucial for NONMEM to correctly process the data stream [19].

2.2 Software and System Requirements NONMEM is written in ANSI Fortran 95 and requires a compatible compiler (e.g., Intel Fortran, gFortran) [20]. As model estimation can be computationally intensive, a fast machine with at least 1-2 GB of dedicated memory is recommended [20]. The software is licensed annually through ICON plc [20]. Effective analysis is facilitated by a suite of supporting tools:

Table 2: Supporting Software Ecosystem for NONMEM Workflow

Tool Category	Example Software	Primary Function
Graphical User Interface (GUI)	Pirana, Census 2 [34]	Provides an environment to run, manage, and edit models, and interpret output.
Scripting & Automation	Perl Speaks NONMEM (PsN) [19] [34]	Aids in model development through tools for validation (bootstrap, VPC), covariate screening, and data handling.
Statistical & Graphical Analysis	R (with packages like xpose, IQRtools) [35] [34]	Used for data preparation, exploratory analysis, generation of diagnostic plots, and custom post-processing.
Code Editor	Notepad++ (with NONMEM syntax highlighting) [35]	Facilitates writing and debugging control stream files.

Core Experimental Protocol for MM Analysis

This protocol outlines the steps to implement and estimate a Michaelis-Menten model in NONMEM, based on best practices and simulation studies [10].

3.1 Control Stream Configuration for MM Kinetics The control stream (filename.ctl) directs all modeling actions. Key code blocks for a basic MM model are:

• $PROB: Define the problem title.
• $INPUT: List the data items (ID, TIME, AMT, DV, CMT, EVID, ...) in the exact order they appear in the data file.
• $DATA: Specify the data file name and options (e.g., IGNORE=@ to ignore header lines).
• $SUBROUTINE: Select ADVAN10 for a one-compartment model with Michaelis-Menten elimination and TRANS1 [19]. This directly provides the parameters VM (Vmax) and KM (Km).
• $PK: Define the population (typical) parameters and inter-individual variability (IIV).

• $ERROR: Define the residual error model. For MM analysis, a combined additive and proportional error model is often appropriate [10]:

• $THETA, $OMEGA, $SIGMA: Provide initial estimates for fixed effects (THETAs), variances of IIV (OMEGAs), and residual error (SIGMA).
• $ESTIMATION: Choose the estimation method. For MM models, First Order Conditional Estimation with interaction (FOCEI) or the more advanced Stochastic Approximation Expectation-Maximization (SAEM) are recommended [32] [10].

3.2 Workflow Diagram: From Data to Validated Model The following diagram illustrates the iterative, cyclical workflow for population PK/PD model development in NONMEM, from data preparation to final model validation [35].

Diagram: Iterative Workflow for Population PK/PD Model Development

3.3 Selection of Estimation Method The choice of estimation algorithm is critical for accurate MM parameter estimation. A simulation study demonstrated that nonlinear methods in NONMEM outperform traditional linearization techniques (Lineweaver-Burk, Eadie-Hofstee) [10].

Table 3: Comparison of Estimation Methods for MM Parameters [32] [10]

Method	Description	Key Characteristic	Suitability for MM
First Order (FO)	Linearizes inter- and intra-individual variability.	Fast but approximate; biased with high variability/sparse data.	Low - Not recommended for final estimation.
FOCE with Interaction	Conditional estimation linearizing residual error.	More accurate than FO for most problems.	High - Standard reliable choice.
Laplace	Similar to FOCE but uses second-order approximation.	Used for highly nonlinear models or non-normal data.	Medium - Can be tried if FOCE fails.
Stochastic Approximation EM (SAEM)	Monte Carlo method using Markov Chain sampling.	Accurate for complex models; handles sparse data well.	Very High - Often optimal for MM kinetics [32] [10].
Importance Sampling (IMP)	Monte Carlo EM method sampling around the mode.	Provides precise objective function value.	High - Good for final evaluation after SAEM.
Iterative Two Stage (ITS)	Approximate EM method using conditional modes.	Faster than FOCE but less accurate for sparse data.	Medium - Useful for initial exploratory runs.

Based on the comparative study, the SAEM method (available in NONMEM 7.6) followed by a final IMP evaluation is highly recommended for MM analysis as it provides the most accurate and precise estimates, especially with realistic combined error structures [32] [10].

3.4 Model Components and Parameter Relationships A clear understanding of the model components and their mathematical relationships is fundamental. The following diagram depicts the structure of a one-compartment model with Michaelis-Menten elimination and the flow of parameters through the modeling process.

Diagram: Components and Relationships in a Michaelis-Menten PK Model

Validation and Diagnostic Protocol

4.1 Standard Model Evaluation Metrics A robust MM model must pass several diagnostic checks [35]:

• Successful Estimation: Minimum of the objective function found, with successful covariance step.
• Parameter Precision: Relative standard errors (RSE%) for fixed and random effects typically <30-50%.
• Diagnostic Plots: Observations vs. Population (PRED) and Individual (IPRED) predictions should be scattered evenly around the line of identity. Conditional weighted residuals (CWRES) vs. PRED or TIME should be randomly scattered around zero.
• Visual Predictive Check (VPC): A simulation-based check where the majority of observed data falls within the prediction intervals of simulated data, confirming the model adequately describes central tendency and variability.

4.2 Simulation-Based Validation (Bootstrap) Internal validation is performed using the nonparametric bootstrap [35]:

• Resample: Generate 500-1000 bootstrap datasets by randomly sampling subjects with replacement from the original dataset.
• Refit: Re-estimate the final model on each bootstrap dataset.
• Analyze: Calculate the median and 95% confidence interval of the parameter estimates from all successful runs. Compare these intervals with the original parameter estimates; close agreement indicates model stability.

4.3 Quantitative Validation from Comparative Studies A simulation study provides quantitative benchmarks for expected performance. When estimating MM parameters from in vitro-like elimination kinetic data, NONMEM's nonlinear methods (NM in the study) showed superior accuracy and precision [10].

Table 4: Validation Metrics from Simulation Study [10]

Estimation Method	Accuracy (Median Bias)	Precision (90% CI Width)	Key Finding
NONMEM (NM)	Lowest bias	Narrowest CI	Most reliable and accurate method.
Traditional Linearization (LB, EH)	Higher bias	Wider CI	Performance worsens with combined error models.
Other Nonlinear Regression (NL, ND)	Moderate bias	Moderate CI	Better than linearization but inferior to NM.

This evidence strongly supports the use of NONMEM's full time-course nonlinear estimation over methods relying on initial velocity calculations or linear transformations for MM analysis [10].

The Scientist's Toolkit for MM Analysis

Table 5: Essential Research Reagent Solutions and Materials

Tool/Resource	Category	Function/Explanation
NONMEM 7.6+	Core Software	Industry-standard engine for nonlinear mixed-effects modeling. Essential for population MM parameter estimation [20] [32].
Pirana	Workflow GUI	Manages run execution, output comparison, and integrates with PsN/R. Critical for organizing complex modeling projects [34].
Perl Speaks NONMEM (PsN)	Automation Toolkit	Executes essential validation techniques like bootstrap and VPC. Required for rigorous model qualification [35] [34].
R with xpose/ggplot2	Diagnostic Graphics	Creates standardized diagnostic plots (e.g., OV vs. PRED, CWRES) for model evaluation and publication [35].
Simulated MM Datasets	Validation Reagent	Used for method qualification and troubleshooting. The study by Cho et al. (2018) provides an excellent template for generating validation data [10].
SAEM Estimation Method	Algorithm	The preferred estimation method in NONMEM for MM models due to its accuracy in handling nonlinear kinetics and combined error structures [32] [10].
Fractional Differential Equation Subroutine	Advanced Tool	For modeling anomalous kinetics (power-law behavior). Useful for extending MM analysis to complex systems where standard ODEs fail [17].
Nonparametric Estimation (NONP)	Diagnostic Tool	Evaluates the shape of parameter distributions. Helps diagnose and correct for bias when inter-individual variability is non-normal [26].

Implementing the Michaelis-Menten Model in NONMEM: Code, Estimation, and Application

Within the specialized field of pharmacometrics, the accurate estimation of Michaelis-Menten (MM) parameters (VM and KM) is critical for characterizing the nonlinear, saturable elimination kinetics exhibited by numerous therapeutic agents. This application note is framed within a broader thesis investigating advanced methodologies for MM parameter estimation using NONMEM (NONlinear Mixed Effects Modeling), the industry-standard software for population pharmacokinetic/pharmacodynamic (PK/PD) analysis [19]. While NONMEM's PREDPP library provides a dedicated, analytically solved one-compartment MM model (ADVAN10), complex real-world scenarios—such as multi-compartment distribution with MM elimination or intricate absorption models—necessitate a more flexible approach [36] [37]. This document details the implementation of these complex MM structures using PREDPP's general differential equation solvers (ADVAN6, ADVAN8, ADVAN13, etc.) and the $DES subroutine, bridging a gap between standard functionality and advanced research needs [38] [39]. The protocols herein are designed for researchers and drug development professionals requiring robust, customizable models for precise parameter estimation.

Core Components: PREDPP, ADVAN, and $DES

The NONMEM system consists of three primary components: the estimation engine (NONMEM), the translator (NM-TRAN), and the pharmacokinetic prediction suite (PREDPP) [18]. PREDPP contains a library of ADVAN (ADVANCE) subroutines, each representing a specific PK model or class of models [40] [41]. The user selects an ADVAN via the $SUBROUTINES record in the control stream.

Table 1: Key PREDPP ADVAN Subroutines for Linear and Michaelis-Menten Kinetics

ADVAN	Model Description	Solution Type	Basic Parameters (TRANS1)	Typical Use Case
ADVAN1	One-compartment linear	Analytical	K, V	Simple IV bolus kinetics [40] [19]
ADVAN2	One-compartment with 1st-order absorption	Analytical	KA, K	Oral dosing [40] [19]
ADVAN3	Two-compartment linear	Analytical	K, K12, K21	IV bolus with distribution [40] [19]
ADVAN10	One-compartment with Michaelis-Menten elimination	Analytical	VM, KM	Standard saturable elimination [40] [37]
ADVAN5/7	General linear model (up to 999 comps)	Matrix Exponential	User-defined	Complex linear compartmental structures [36] [38]
ADVAN6/8/13	General nonlinear model	ODE Solution	User-defined	Custom MM models, complex kinetics [38] [37]

For models beyond the predefined set (ADVAN1-4, 10-12), PREDPP offers general subroutines. ADVAN6, ADVAN8, and ADVAN13 are used for models defined by ordinary differential equations (ODEs) [38] [37]. When using these, the user must provide a $DES block in the control stream (or a separate DES Fortran subroutine). This block contains the code that defines the right-hand side of the differential equations governing drug movement between compartments [39]. This is the essential mechanism for coding custom MM elimination within a multi-compartment structure or alongside other nonlinear processes.

Workflow for Selecting ADVAN Subroutines for Michaelis-Menten Models

Methodology: Coding MM Elimination with $DES

The implementation of a user-defined MM model involves a sequential configuration of NM-TRAN records. The following protocol outlines the steps for coding a two-compartment model with Michaelis-Menten elimination from the central compartment.

Step 1: Define the Model Structure with $MODEL The $MODEL block declares the number and type of compartments. For a two-compartment mammillary model with a peripheral tissue compartment and an optional output compartment, the code is:

Step 2: Select a General Nonlinear ADVAN The $SUBROUTINES record specifies the ODE solver. ADVAN13 (using LSODA) is often preferred for its ability to handle both stiff and non-stiff equations efficiently [37].

The TOL value controls the numerical integration precision [38].

Step 3: Declare and Assign Parameters in $PK The $PK block is used to define the model's parameters, including fixed effects, random effects (ETAs), and covariate relationships. Typical parameters for this model include central volume (V1), inter-compartmental clearance (Q), peripheral volume (V2), and the MM parameters (VM, KM).

Step 4: Code the Differential Equations in $DES This is the core of the custom model. The $DES block calculates the derivative (DADT) for each compartment amount (A). For the two-compartment MM model:

The equation MM_RATE implements the standard Michaelis-Menten velocity equation, where the rate of elimination is a function of the amount A(1) in the central compartment [17] [39].

Step 5: Define the Observation Model in $ERROR Finally, the $ERROR block links the model predictions to the observed data, typically defining a residual error model.

Two-Compartment Model with Michaelis-Menten Elimination Pathway

Application Protocols and Parameter Estimation

Protocol for a Complex Absorption MM Model

Chatelut et al. (1999) modeled the absorption of alpha interferon using simultaneous first-order and zero-order processes into a one-compartment body with linear elimination [38]. Adapting this for MM elimination demonstrates the flexibility of the $DES approach.

Experimental Methodology & NM-TRAN Implementation:

• Model Schematic: Two parallel depot compartments (DEPOT1 for first-order, DEPOT2 for zero-order absorption) feed into a central compartment with MM elimination.
• $MODEL: Define three compartments: DEPOT1, DEPOT2, CENTRAL.
• $PK: Declare parameters: KA (first-order absorption rate), D2 (zero-order absorption duration), FZ (fraction absorbed via first-order), VM, KM, V.
• $DES Code:

• Data File: Requires two dosing records per dose: one to CMT=1 (amount = FZDOSE) and one to CMT=2 (amount = (1-FZ)DOSE).

Protocol for MM Parameter Estimation Methods

Accurate estimation of VM and KM is computationally challenging due to the nonlinearity. The choice of estimation algorithm in NONMEM is critical.

Table 2: Comparison of NONMEM Estimation Methods for Michaelis-Menten Models

Method	Principle	Advantages for MM	Disadvantages for MM	Recommended Use
First Order (FO)	Linearizes random effects around zero [32].	Fastest computation.	High bias with large inter-individual variability or sparse data [32].	Initial model exploration only.
First Order Conditional Estimation (FOCE)	Linearizes around conditional estimates of ETAs [32].	More accurate than FO, standard for nonlinear PK.	May fail with high residual error or severe nonlinearity.	Standard choice for most MM models with rich data.
FOCE with INTERACTION	Accounts for interaction between inter- and intra-individual error [32].	Improved accuracy when residual error is large.	Slightly slower than FOCE.	Default choice for final MM model estimation.
Importance Sampling (IMP) / SAEM	Monte Carlo methods for exact likelihood evaluation [32].	Most accurate for complex nonlinearities and sparse data.	Computationally intensive, stochastic variability in estimates.	Complex models, problematic convergence with FOCE.

Recommended Estimation Protocol:

• Initialization: Use literature or naive pooled estimates for THETA initial values. Set OMEGA diagonal elements to moderate values (e.g., 0.09 for 30% CV).
• Step 1 - Preliminary Exploration: Run FO estimation to check data structure and identify obvious problems.
• Step 2 - Base Model Estimation: Switch to FOCE with INTERACTION. Ensure successful termination and examine gradient messages.
• Step 3 - Covariate Modeling: Continue with FOCE-INTERACTION to test significant covariates on parameters like VM.
• Step 4 - Final Validation: If convergence is difficult or data are sparse, confirm final parameter estimates using a Monte Carlo method (IMP or SAEM) [32].

Advanced Applications and the Scientist's Toolkit

Incorporating Fractional Differential Equations (FDEs)

Recent research extends nonlinear mixed-effects modeling to systems defined by Fractional Differential Equations (FDEs), which describe anomalous kinetics and memory effects [17]. A one-compartment model with MM elimination can be reformulated as a fractional FDE:

where ^C_0D^α_t is the Caputo fractional derivative of order α (0<α<1) [17]. Implementing this in NONMEM requires a user-supplied subroutine that replaces the $DES block with a numerical solver for FDEs, demonstrating the extensibility of the platform for cutting-edge MM research [17].

The Scientist's Toolkit: Essential Components

Table 3: Research Reagent Solutions for MM Modeling with $DES

Tool/Component	Function in MM Model Development	Key Considerations
PREDPP Library (ADVAN10)	Provides a pre-built, analytically solved one-compartment MM model for validation and comparison [40] [37].	Serves as a benchmark for custom $DES models.
General Nonlinear ADVAN (6,8,13)	Provides the ODE solver framework necessary for implementing custom MM structures [38] [37].	Choice depends on model stiffness; ADVAN13 (LSODA) is often robust.
$DES Block	The core "reagent" for coding the differential equations that define the custom MM kinetic process [39].	Must correctly calculate derivatives DADT. Use compact array format for large models.
TOL Option	Sets the tolerance for the numerical ODE solver, controlling precision and stability [38] [37].	A value of 4-6 is typical. Adjust if runs fail due to integration error.
MU Referencing	A coding technique (using MU_ prefix) that improves estimation efficiency, especially with EM methods [32].	Highly recommended for complex models to speed up convergence.
PDx-Pop, Pirana, PsN	Third-party modeling environments that provide workflow management, visualization, and automated tools (e.g., VPC, bootstrap) [19].	Essential for efficient, reproducible, and robust model development.

Implementing Michaelis-Menten pharmacokinetics using the $DES subroutine and general ADVANs in PREDPP unlocks a powerful paradigm for pharmacometric research. This approach transcends the limitations of precompiled solutions, allowing researchers to construct and estimate parameters for sophisticated, mechanism-based models that accurately reflect complex biological processes—from multi-compartment saturation kinetics to parallel absorption pathways. Mastery of this technique, combined with a strategic understanding of estimation algorithms and diagnostic tools, positions scientists to tackle challenging nonlinear PK problems, ultimately contributing to more informed drug development decisions and optimized therapeutic regimens. The methodologies outlined here provide a foundational protocol that can be adapted and extended as part of an advanced thesis in modern pharmacometric analysis.

Within the broader thesis on advanced pharmacometric modeling using NONMEM, the generation of robust initial estimates for Michaelis-Menten parameters—the maximum elimination rate (Vmax) and the substrate concentration at half Vmax (Km)—is not a mere preliminary step but a critical determinant of research success. Nonlinear mixed-effects models, which are fundamental to population pharmacokinetic (PK) analysis, are inherently dependent on adequate initial parameter estimates for efficient and correct convergence of the estimation algorithm [42]. Poor initial estimates can lead to failed minimization, termination at local minima yielding biologically implausible parameter values, or protracted model-building cycles plagued by instability [43].

This challenge is particularly acute for Michaelis-Menten kinetics, a cornerstone model for characterizing saturable enzymatic elimination. The parameters Vmax and Km are often correlated, and their estimation can be sensitive to the design and quality of the data [13]. Framed within a thesis exploring NONMEM's full potential, this document provides detailed application notes and protocols. It moves beyond simplistic rule-of-thumb guesses, presenting a systematic, multi-strategy toolkit for generating scientifically defensible initial estimates. These strategies are designed to enhance model reliability, reduce development time, and form the foundation for robust covariate analysis and clinical simulations in model-informed drug development [43] [44].

Computational Foundations: NONMEM and Michaelis-Menten Kinetics

2.1 NONMEM Architecture for PK Modeling NONMEM (NONlinear Mixed Effects Modeling) is a software program that fits PK/PD models to data while accounting for inter-individual and intra-individual variability [19]. Its workflow involves a control stream (.ctl file), a data file, and output files. The control stream specifies the model, parameters, and estimation methods. A key component is PREDPP, a library of pre-compiled PK models accessed via the $SUBROUTINES record using ADVAN and TRANS subroutines [19].

2.2 Implementing Michaelis-Menten Elimination in NONMEM For Michaelis-Menten kinetics, the ADVAN10 subroutine is used in conjunction with TRANS1. This specifies a one-compartment model with Michaelis-Menten elimination from the central compartment. The two basic parameters defined in the $PK block are VM (Vmax) and KM (Km) [19]. The structural model is defined by the differential equation: dA/dt = - (VM * A/V) / (KM + A/V), where A is the amount in the central compartment and V is the volume of distribution. Proper data setup is crucial: the dataset must include ID, TIME, AMT (dose), DV (observed concentration), EVID (event identifier), and MDV (missing dependent variable) items, with records sorted by ID and TIME [45].

2.3 The Imperative for Robust Initial Estimates The estimation process in NONMEM is an iterative search for parameter values that minimize an objective function value (OFV). The landscape of this search can be complex, with multiple local minima. Initial estimates that are far from the true values can cause the algorithm to fail to converge or to converge to an incorrect solution [43] [46]. This is formally linked to the balance between model complexity and the information content of the data; an over-parameterized model relative to the data will exhibit instability, for which poor initial estimates are a primary catalyst [43]. Therefore, a robust initialization strategy directly addresses the root cause of a common class of model instability issues.

Strategic Framework for Generating Initial Estimates

A multi-faceted approach is recommended, moving from simple, data-informed guesses to sophisticated, automated procedures. The choice of strategy depends on data type (rich vs. sparse, in vitro vs. in vivo), available prior knowledge, and the stage of analysis.

3.1 Strategy 1: Prior Knowledge and Literature-Based Anchoring The first and most straightforward strategy involves leveraging existing knowledge.

• Published Values: For a known enzyme or transporter, literature values for Km and Vmax (often scaled to per mg protein or per cell) can provide an order-of-magnitude starting point. Allometric scaling (e.g., using body weight exponents of 0.75 for clearance) may be applied to extrapolate in vitro Vmax to an in vivo whole-organ value [44].
• Related Compounds: Data for structurally or mechanistically similar compounds can offer plausible ranges.
• Biological Plausibility: Estimates should be checked for biological sense (e.g., Km should be within or near the range of observed substrate concentrations).

3.2 Strategy 2: Data-Driven Methods from In Vitro and Rich Data For in vitro enzyme kinetic studies or rich in vivo PK data, direct graphical or computational analysis can yield excellent initial estimates.

• Non-Compartmental Analysis (NCA): For in vivo data following a single dose, NCA can estimate total clearance (CL) and the area under the curve (AUC). At low, non-saturating concentrations, clearance is approximated by Vmax/Km. A rough estimate can be obtained: Km ≈ Dose / (2 * Vd), and Vmax ≈ CL * Km, where Vd is the volume of distribution from NCA [42].
• Visual Inspection of Saturation: Plotting elimination rate (or observed concentration-time slope) against concentration can visually indicate the range of Km (concentration where the rate is at half-maximum) and Vmax (the plateau rate).
• Linearized Plots (For In Vitro Data Only): While final estimation should use nonlinear methods, linear transformations like the Lineweaver-Burk (1/v vs. 1/[S]) or Eadie-Hofstee (v vs. v/[S]) plot can provide quick, albeit statistically biased, initial guesses from in vitro velocity data [13].

3.3 Strategy 3: Automated and Preconditioning Pipelines For population modeling with sparse data or during automated model development, algorithmic generation of initial estimates is essential.

• Automated Base Model Pipelines: Recent research has developed integrated pipelines that use data-driven algorithms to compute initial estimates for both structural and statistical parameters. These pipelines perform well with both rich and sparse data scenarios, generating estimates that lead to final parameters closely aligned with true or literature values [42].
• Preconditioning with Simplified Models: A highly effective strategy is to "precondition" the problem by first fitting a simpler, more stable model.
  • Fit a linear elimination model (e.g., ADVAN1 or ADVAN2) to obtain estimates for clearance (CL) and volume (V).
  • Fix the volume parameter (V) from the linear model. Use the final CL estimate as an initial estimate for the ratio Vmax/Km.
  • Provide an initial Km estimate that is within the range of observed concentrations (e.g., the median observed concentration).
  • Calculate the corresponding Vmax initial estimate as CL * Km.
  • Fit the full Michaelis-Menten model (ADVAN10), freeing all parameters. This sequential approach often leads to more stable convergence than starting with naïve guesses.

Table 1: Comparison of Estimation Method Performance for Michaelis-Menten Parameters (Simulation Study) [13]

Estimation Method	Description	Key Advantage	Key Limitation	Relative Performance (Accuracy & Precision)
Lineweaver-Burk (LB)	Linear fit to 1/v vs. 1/[S] plot.	Simple, visual.	Prone to statistical bias; poor error model assumption.	Least accurate, especially with high variability.
Eadie-Hofstee (EH)	Linear fit to v vs. v/[S] plot.	Less bias than LB.	Still assumes erroneous error structure.	Low to moderate accuracy.
Nonlinear Regression (NL)	Direct nonlinear fit of v to [S] data.	Correct error structure.	Requires initial velocity data, discards time-course info.	High accuracy.
Nonlinear Dynamic (NM)	Nonlinear fit of full [S]-time course data (e.g., via NONMEM).	Uses all data; correct error model; estimates in vitro half-life.	Requires appropriate software; needs careful initialization.	Most accurate and precise, superior with combined error models.

Detailed Experimental Protocols

4.1 Protocol 1: Generating and Analyzing In Vitro Kinetic Data for Initial Estimates

• Objective: To obtain initial estimates for Vmax and Km from an in vitro drug elimination experiment using primary hepatocytes or microsomes.
• Materials: See "The Scientist's Toolkit" below.
• Workflow:
  • Incubation: Incubate the test compound at 5-8 different substrate concentrations (spanning expected Km) with the enzyme system. Use a short, linear time course (e.g., 5-7 time points per concentration).
  • Data Generation: Quench reactions and quantify substrate depletion or metabolite formation. Calculate the initial velocity (v) for each [S] using linear regression of amount vs. time for the early, linear phase.
  • Initial Estimate Calculation:
    • Method A (Linearization): Create an Eadie-Hofstee plot (v vs. v/[S]). Perform a linear regression. The y-intercept is Vmax. The slope is -Km.
    • Method B (Direct Plot): Plot v vs. [S]. Visually estimate Vmax (plateau) and Km (concentration at half Vmax).
  • NONMEM Preparation: Format a dataset with columns: ID (incubation ID), TIME, CONC ([S]), DV (measured concentration), EVID, MDV. Use EVID=0 for observations.
  • Control Stream Setup: Use $SUBROUTINES ADVAN10 TRANS1. In $PK, declare VM = THETA(1) * EXP(ETA(1)) and KM = THETA(2) * EXP(ETA(2)). Input the graphical estimates as initial values for THETA(1) and THETA(2).
• Validation: The final NONMEM estimates from the full time-course analysis (NM method) should be more reliable than the graphical initials [13].

4.2 Protocol 2: Preconditioning Strategy for In Vivo Population PK Analysis

• Objective: To generate robust initial estimates for a population Michaelis-Menten model using clinical PK data.
• Workflow Diagram:

• Protocol Steps:
  • Data Preparation: Ensure the dataset is correctly formatted for PREDPP: sorted by ID and TIME, with proper EVID and MDV flags [45].
  • Linear Model Fit:
    • Build a one- or two-compartment linear model (ADVAN1/ADVAN2 or ADVAN3/ADVAN4).
    • Use reasonable initials (e.g., from NCA or literature).
    • Run the model to successful convergence. Document the final estimates for clearance (CL) and central volume (V).
  • Calculate Michaelis-Menten Initials:
    • Set Km_initial to the median of the observed concentrations (DV where EVID=0).
    • Calculate Vmax_initial = CL_final * Km_initial.
  • Build and Run Michaelis-Menten Model:
    • Create a new control stream using $SUBROUTINES ADVAN10 TRANS1.
    • In the $PK block, define:

    • On the $THETA record, set: (Vmax_initial, , ) (Km_initial, , ) (V_final, FIXED).
    • Run the model. The successful convergence of this preconditioned model provides the final robust parameter estimates.

Table 2: Key Diagnostic Outputs from NONMEM for Validating Model Convergence [46]

Output File/Item	Description	Interpretation for Successful Convergence
Report (.lst/.res) File	Primary results file.	Check for MINIMIZATION SUCCESSFUL and absence of severe warnings.
Objective Function Value (OFV)	-2 log-likelihood.	Should stabilize at final iteration. Large changes indicate problems.
Parameter Estimates (THETA)	Final population parameter values.	Should be biologically plausible and have reasonable precision.
Standard Errors	Precision of THETA estimates.	Relative standard error (RSE) < 30-50% often desired. Failed covariance step may indicate instability.
Gradients	Derivative of OFV w.r.t parameters at solution.	All gradients should be near zero (e.g., < 0.001).
.ext File	Final estimates table.	Contains termination codes, OFV, and parameter estimates for easy extraction.
.phi File	Individual parameter estimates (ETA).	Useful for diagnosing individual fit problems and visualizing IIV.

The Scientist's Toolkit

Table 3: Essential Research Reagent Solutions and Computational Tools

Item	Function in Initial Estimate Generation
Graphical/Analysis Software (R, Python)	For data preprocessing, NCA, creating diagnostic plots (Eadie-Hofstee), and running automated estimation pipelines [42] [13].
NONMEM Software	Industry-standard platform for nonlinear mixed-effects modeling. The ADVAN10 subroutine is specifically designed for Michaelis-Menten kinetics [19].
PKNCA R Package	Performs Non-Compartmental Analysis to obtain CL and AUC, which inform the Vmax/Km ratio [42].
Automated Pipeline Scripts	Custom or published R scripts that algorithmically derive initial estimates for structural and statistical parameters from the dataset, reducing manual guesswork [42].
Diagnostic Toolkit (Xpose, Pirana)	Assists in evaluating model convergence, goodness-of-fit, and comparing OFV between linear and nonlinear models, confirming the need for Michaelis-Menten kinetics.
Estimation Algorithms (FOCE, SAEM)	Within NONMEM, the First Order Conditional Estimation (FOCE) and Stochastic Approximation EM (SAEM) methods are robust algorithms for fitting nonlinear models like Michaelis-Menten [13].

Diagram: NONMEM Michaelis-Menten Model Specification & Estimation Workflow

Within the context of a broader thesis on Michaelis-Menten parameter estimation research using NONMEM, the selection of an appropriate estimation algorithm is not merely a technical step but a foundational scientific decision. Nonlinear mixed-effects (NLME) modeling in pharmacometrics aims to identify the population parameters (THETAs, OMEGAs, SIGMAs) that best describe the observed data while accounting for inter-individual (ETA) and residual (EPS) variability [32]. The core computational challenge lies in evaluating the integral over all possible individual parameter values for each subject [32]. Different estimation methods solve this problem with distinct algorithmic strategies, leading to significant differences in performance, reliability, and efficiency [47] [48] [49].

For researchers focused on enzyme kinetics, particularly the estimation of V~max~ and K~m~ via the Michaelis-Menten equation, this choice is critical. While traditional linearization methods (e.g., Lineweaver-Burk) are available, nonlinear estimation methods within NONMEM provide more reliable and accurate parameter estimates, especially when data incorporates complex error structures [24]. This article provides a detailed comparison of four key estimation families in NONMEM: First-Order Conditional Estimation (FOCE), Importance Sampling Expectation-Maximization (IMP), Stochastic Approximation Expectation-Maximization (SAEM), and Bayesian (BAYES) approaches. It offers application notes, experimental protocols, and practical guidance to inform method selection within advanced pharmacometric research.

Characteristics and Algorithmic Foundations of Estimation Methods

2.1 First-Order Conditional Estimation (FOCE) FOCE is a classical maximum-likelihood method that approximates the likelihood integral. It evaluates the mode (most likely values) of the individual parameters (ETAs) and uses a first-order (linear) approximation of the variance around this mode to estimate the integral [32]. The INTERACTION option (often termed FOCE-I) accounts for correlation between inter-individual and residual error and is recommended when residual error is proportional [49]. While faster than exact methods for simpler problems, its approximation can lead to inaccuracies or convergence failures with complex models, high inter-individual variability, or sparse data [48] [32]. The FAST option can significantly reduce run time by leveraging a specific model structure [48] [49].

2.2 Expectation-Maximization (EM) Methods: IMP and SAEM EM methods are "exact" algorithms that perform a Monte Carlo integration to explore the entire ETA space [32]. They consist of an Expectation (E) step, which evaluates the integral, and a Maximization (M) step, which updates the population parameters.

• Importance Sampling (IMP): The E-step uses a normal sampler centered at the mode (or mean) of the conditional density, focusing on the "important" region of the parameter space. It provides accurate objective function values and standard errors directly [32].
• Stochastic Approximation EM (SAEM): This method uses a Markov Chain Monte Carlo (MCMC) sampler. It often runs in two phases: a first phase with rapid parameter updates and a second phase where individual parameter samples are averaged for convergence. SAEM itself does not evaluate the objective function; a final IMP EONLY=1 step is typically used to obtain it [47] [32].

2.3 Bayesian (BAYES) Approach The Bayesian method in NONMEM employs MCMC sampling to characterize the full posterior distribution of the parameters, given the data and prior information [20] [50]. It is particularly useful for complex models where maximum likelihood methods struggle, for incorporating prior knowledge, and for directly quantifying parameter uncertainty. Unlike EM methods that seek a single "most likely" estimate, BAYES generates a large sample of probable parameter sets [50].

2.4 Software and System Context All these methods are implemented in NONMEM, the industry-standard software for population PK/PD analysis [20]. The software comprises the NONMEM engine, the PREDPP subroutine library for PK models, and the NM-TRAN preprocessor [20]. The choice of estimation method interacts with the model definition, particularly the selection of $SUBROUTINE (e.g., analytical ADVAN routines vs. differential equation solver ADVAN13), which dictates whether the problem is solved analytically or via numerical integration [49].

Table 1: Core Characteristics of NONMEM Estimation Methods [47] [48] [32]

Method	Algorithmic Class	Key Algorithmic Feature	Computational Demand	Typical Convergence Behavior	Objective Function (OFV)
FOCE(-I)	Classical MLE	First-order approximation around ETA mode.	Low to Moderate for simple models; increases with complexity.	Can fail with complex models, sparse data, or high IIV.	Directly estimated, used for hypothesis testing (LRT).
IMP	Exact Monte Carlo EM	Importance sampling from a normal proposal density.	High (requires many samples per subject).	Robust for complex models; sensitive to model misspecification [48].	Directly estimated, used for hypothesis testing (LRT).
SAEM	Exact Monte Carlo EM	MCMC sampling with stochastic approximation.	Moderate to High.	Robust; benefits from ITS or parameter log-transform for difficult problems [47].	Not directly estimated; requires a final IMP EONLY step.
BAYES	Bayesian MCMC	Full posterior sampling via MCMC (NUTS).	Very High.	Robust for complex models; requires careful chain diagnostics.	Not applicable; inference based on posterior distributions.

Performance Comparison and Selection Guidelines

3.1 Empirical Findings from Comparative Studies Research indicates that the optimal method is highly context-dependent. For relatively simple PK models (e.g., one- or two-compartment) with rich data, FOCE and FOCE FAST are often the most efficient, providing precise estimates with the shortest run times [48]. However, for complex models—such as target-mediated drug disposition (TMDD), parent-metabolite systems, or models with data below the quantification limit (BLQ)—EM and Bayesian methods show superior reliability.

A study on a TMDD model with limited data (15 subjects) found IMP and IMPMAP to be the most robust, achieving stable convergence where FOCE succeeded in only 21% of runs [47]. SAEM, while sometimes having initial convergence issues, produced the most accurate individual parameter estimates (posthocs) when it did converge [47]. Another study on a complex parent-metabolite model confirmed that FOCE could fail to reliably assess parameter precision, while IMP and SAEM performed well, with SAEM being faster [48].

For Michaelis-Menten parameter estimation specifically, a simulation study demonstrated that nonlinear estimation methods in NONMEM provided more accurate and precise estimates of V~max~ and K~m~ compared to traditional linearization methods, particularly under a combined error model [24].

3.2 Selection Framework and Practical Recommendations Method selection should be guided by model complexity, data structure, and project goals.

Table 2: Estimation Method Selection Guide [47] [48] [32]

Scenario	Recommended Primary Method(s)	Rationale and Practical Notes
Simple PK Model (1-2 CMTs), Rich Data	FOCE-I (with FAST option)	Fastest and most efficient. Use as benchmark.
Complex Model (TMDD, ODEs, >6 params)	SAEM or IMP	More reliable convergence. Start SAEM, use IMP EONLY for final OFV.
Sparse Data or High IIV	SAEM or IMP	Better handles poor parameter identifiability.
Model with BLQ Data	SAEM or IMP	More accurately handles censored data likelihood.
Small Sample Size (N<10)	FOCE-I or BAYES	One study found FOCE-I more reliable than BAYES for very small N with simple models [50].
Including Prior Information	BAYES	Natural framework for incorporating prior knowledge from literature or previous studies.
Initial Model Exploration	ITS	Very fast approximate EM method for initial screening [32].
Final Model Refinement & Covariate Testing	IMP	Provides a stable, exact OFV for likelihood ratio tests.

General Workflow Advice:

• Start Simple: Use FOCE-I for initial model building.
• Switch for Complexity: If FOCE fails to converge or yields unstable covariance steps, switch to SAEM.
• Finalize with IMP: Use SAEM for estimation, followed by a final IMP EONLY=1 step with MAXEVAL=0 to obtain the OFV and standard errors for final reporting and hypothesis testing [47] [32].
• Utilize Parallel Computing: For IMP or SAEM, use parallel computing (NPROC) to significantly reduce runtime [20] [48].

Experimental Protocols for Method Comparison

4.1 Protocol 1: Simulation-Based Comparison for a Michaelis-Menten Elimination Model This protocol is designed to evaluate method performance for a core thesis model.

• Objective: To compare the bias, precision, and convergence rate of FOCE, IMP, SAEM, and BAYES in estimating V~max~ and K~m~ under varying levels of inter-individual variability (IIV) and residual error.
• Model: A one-compartment model with intravenous bolus administration and Michaelis-Menten elimination (e.g., using ADVAN10 or ADVAN13 with $DES) [49] [51]. Parameters: V~max~ (typical value), K~m~ (typical value), volume of distribution (V). IIV (log-normal) is assumed on V~max~ and K~m~.
• Simulation Design:
  • Subjects: Simulate 50 datasets each for N=15 (sparse) and N=50 (rich).
  • Variability: Cross three levels of IIV (CV% = 20%, 50%, 80%) with two residual error models (additive and proportional).
  • Software: Use $SIMULATION in NONMEM or the modelr package in R for data generation.
• Estimation: Fit each simulated dataset using all four methods.
  • FOCE: METHOD=CONDITIONAL INTERACTION MAXEVAL=9999 SIGL=9
  • IMP: METHOD=IMP ISAMPLE=1000 NITER=1000
  • SAEM: METHOD=SAEM NBURN=500 NITER=500 followed by METHOD=IMP ISAMPLE=1000 NITER=0 EONLY=1
  • BAYES: METHOD=BAYES NUTS
• Outcome Measures:
  • Convergence Rate: Percentage of successful minimizations per method/scenario.
  • Bias: Median relative estimation error (REE) for each parameter: (Estimate - True Value) / True Value.
  • Precision: Relative Root Mean Square Error (rRMSE).
  • Runtime: Average computation time.

4.2 Protocol 2: Real-Data Application to a Parent-Metabolite PK System This protocol assesses methods in a real-world, complex modeling scenario [48].

• Objective: To evaluate the practical performance of estimation methods on a nonlinear parent-metabolite PK model with potential model misspecification.
• Data: Use rich PK data for oxfendazole and its metabolites (sulfone and sulfoxide) [48].
• Model Development:
  • Build a base model for the parent drug using all methods.
  • Develop a joint model linking parent and metabolites, incorporating formation and elimination pathways.
  • Test the need for pre-systemic metabolism (a source of model nonlinearity).
• Estimation Strategy:
  • Run FOCE-I as a baseline. If it fails or shows high RSEs, proceed.
  • Run SAEM to obtain population parameter estimates.
  • Run a final IMP step (EONLY=1) on the SAEM estimates to obtain the OFV and covariance.
  • (Optional) Run BAYES to obtain full posterior distributions and compare with maximum likelihood estimates.
• Comparison Metrics:
  • Success of convergence for the full joint model.
  • Plausibility and precision (RSE%) of parameter estimates.
  • Stability of the covariance matrix.
  • Goodness-of-fit plots (e.g., population and individual predictions vs. observations).

Workflow and Decision Pathways

Diagram 1: Estimation Method Selection Algorithm This flowchart provides a practical decision pathway for selecting an estimation method based on model complexity and initial results, guiding researchers from problem assessment to final reporting [47] [48] [49].

Diagram 2: Michaelis-Menten Parameter Estimation Workflow This diagram outlines the sequential steps for robust Michaelis-Menten parameter estimation, highlighting the hybrid use of estimation methods (FOCE for exploration, SAEM for robustness, IMP for final inference) within a complete model qualification framework [24] [32].

The Scientist's Toolkit: Essential Software and Analysis Tools

Table 3: Essential Research Toolkit for NONMEM Analysis [20] [50] [51]

Tool Name	Category	Primary Function	Role in Estimation Method Research
NONMEM 7.6	Core Engine	Executes NLME model estimation.	Provides all estimation methods (FOCE, IMP, SAEM, BAYES). Essential for protocol execution.
PsN (Perl-speaks-NONMEM)	Workflow Toolkit	Automates model execution, bootstrapping, VPC, SSE.	Critical for running large simulation-estimation studies (Protocol 1) and model qualification.
Pirana	Modeling Environment	GUI for managing NONMEM runs, results, and diagnostics.	Facilitates comparison of outputs from different estimation methods and project management.
R / RStudio	Statistical Computing	Data preparation, result aggregation, custom graphics, statistical analysis.	Used to simulate data, parse NONMEM outputs, calculate performance metrics (bias, rRMSE), and generate comparative plots.
Xpose	R Library	Diagnostics for NLME models.	Generates standard goodness-of-fit plots to compare model performance across methods.
PMX Repository/Code Templates	Code Resource	Provides template control streams for common models.	Offers reliable starting code for models like Michaelis-Menten elimination, reducing setup errors [51].

The accurate characterization of saturable pharmacokinetic (PK) processes, predominantly described by Michaelis-Menten (M-M) kinetics, is a cornerstone of model-informed drug development for compounds exhibiting nonlinear clearance. Within the broader thesis on NONMEM-based M-M parameter estimation, this application note provides detailed protocols for simulating complex concentration-time profiles and predicting transitions into and out of saturable regimes. NONMEM, the industry-standard nonlinear mixed-effects modeling software [20], offers a suite of advanced features—including Bayesian estimation [52], delay differential equation solvers [53] [20], and optimal design evaluation [54]—that are essential for this task. Successful modeling in this context is critically dependent on robust initial parameter estimates to avoid convergence failure [7], careful handling of biological delays [53], and the strategic evaluation of trial designs to ensure parameter identifiability [54]. These protocols integrate contemporary methodologies, including automated estimation pipelines [7] and considerations for Large Language Model-assisted workflows [55], to provide a comprehensive framework for tackling the challenges of saturation kinetics.

Foundational Parameter Estimation Methods

The selection of an initial estimation strategy is pivotal for the subsequent successful estimation of M-M parameters (VM and KM). The following table summarizes the core methodologies, their applications, and key performance metrics based on validation studies.

Table 1: Summary of Initial Parameter Estimation Methods for Michaelis-Menten Modeling [7]

Method Category	Primary Function	Key Equations/Outputs	Applicable Data Scenario	Reported Performance (rRMSE)
Adaptive Single-Point	Estimates CL, Vd, Ka from sparse single-point-per-individual data.	Vd = Dose / C₁; CL = Dose / Css_avg; Ka solved from 1-cpt equations.	Sparse data, single-dose & steady-state.	Final estimates within ±15% of true simulated values.
Naïve Pooled NCA	Provides population PK parameter estimates via non-compartmental analysis on pooled data.	CL = Dose / AUC₀‑∞; Vz = CL / λz.	Rich or pooled sparse data.	Serves as reliable initial estimates for base models.
Graphic Methods	Determines parameters via linear regression of specific PK phases (e.g., terminal elimination).	CL from slope of ln(C) vs. T; Vd ≈ Dose / C₀,extrap; Ka from residual slope.	Rich data, clearly defined phases.	Effective for identifying linear elimination parameters pre-saturation.
Parameter Sweeping	Identifies optimal initial estimates for complex parameters (e.g., VM, KM) by simulating across a defined range.	Tests candidate values; selects set minimizing relative Root Mean Squared Error (rRMSE).	All data types, essential for nonlinear parameters.	Directly optimizes initial guesses for M-M parameters prior to full NONMEM estimation.

Experimental Scenarios for Saturational Transition Analysis

Simulating profiles that transition between linear and nonlinear kinetic zones requires well-defined experimental scenarios. The following table outlines standard and advanced scenarios used to stress-test M-M models and design clinical studies.

Table 2: Experimental Scenarios for Simulating Saturational Transitions

Scenario Type	Primary Objective	Key Design Variables	Typical NONMEM ADVAN/TRANS	Critical Outputs
Rapid IV Bolus (Single Dose)	Characterize intrinsic VM and KM from a wide concentration range.	High dose to ensure initial saturation.	ADVAN13/TRAN6 (General ODE)	Profile shape, time to transition from zero-order to first-order elimination.
Oral Dosing (Multiple Ascending Dose)	Assess saturation in absorption and/or first-pass metabolism.	Dose levels, formulation (Ka), feeding state.	ADVAN13/TRAN6 or ADVAN2 (for 1-cpt oral) [56].	Cmax, AUC nonlinearity, bioavailability (F) changes with dose.
Continuous IV Infusion	Identify steady-state concentration (Css) at which clearance transitions.	Infusion rate (R0), infusion duration.	ADVAN13/TRAN6.	Css, time to reach steady-state, clearance value at Css.
Pulsatile Endogenous System	Model drug effect on an underlying saturable physiological process (e.g., hormone synthesis).	Baseline pulse amplitude, frequency, drug inhibitory IC₅₀ [57].	ADVAN13 or ADVAN16 (for DDEs) [53].	Dampening of pulse amplitude, change in average baseline.
Optimal Design for Parameter Estimation	Optimize sampling schedule to precisely estimate VM and KM [54].	Sample times, number of samples, dose groups.	User-defined (e.g., ADVAN13).	Fisher Information Matrix (FIM), predicted standard errors for VM and KM.

Detailed Experimental Protocols

Protocol 1: Comprehensive Workflow for M-M Model Development in NONMEM

This protocol integrates initial estimation, model coding, and evaluation for a drug exhibiting saturable elimination.

1. Data Preparation and Initial Estimation:

• Standardize the dataset per nlmixr2/NONMEM requirements (ID, TIME, AMT, DV, EVID, MDV) [56].
• Apply the automated estimation pipeline [7]:
  • Use the Naïve Pooled NCA method to obtain initial estimates for linear clearance (CLlinear) and volume (V).
  • Use parameter sweeping to generate initial estimates for VM and KM. Define a plausible range (e.g., VM from 0.5*CLlinear to 10*CLlinear; KM from 0.1*Cmax to 2*Cmax). Simulate the M-M model and calculate rRMSE against observed data to select the best candidate pair.

2. NONMEM Control Stream Development:

• Use a general differential equation solver ($SUBROUTINES ADVAN13 TOL=6).
• Code the M-M elimination in $DES:

• Implement parameters with inter-individual variability (IIV) and covariate relationships in $PK:

• Set initial estimates ($THETA) based on the automated pipeline output and bounds for OMEGA and SIGMA [56].

3. Model Estimation & Evaluation:

• Begin estimation using the First Order Conditional Estimation with interaction (METHOD=1 INTERACTION) [56].
• If convergence is unstable, switch to a Bayesian framework (METHOD=BAYES or METHOD=NUTS) [52] [20] to incorporate prior information (e.g., weakly informative priors on KM from in vitro data).
• Evaluate goodness-of-fit (GOF) plots, parameter precision, and visual predictive checks (VPCs) to ensure the model captures the saturational transition.

Protocol 2: Implementing Delay Models for Saturable Precursor Turnover

Many saturable processes (e.g., production of an endogenous compound) involve significant time delays [53]. This protocol extends a turnover model with M-M synthesis.

1. Model Structure Definition:

• Define a precursor compartment (A(2)) with zero-order synthesis (Kin) and first-order loss (Kout).
• Define the observed response compartment (A(1)) where the input is the delayed output from the precursor pool.

2. Delay Implementation (Choose one):

• Transit Compartment Approach: Insert n transit compartments between A(2) and A(1) to approximate a gamma-distributed delay. The mean transit time (MTT) = n / Ktr, where Ktr is the transit rate [53].
• Delay Differential Equation (DDE) Approach (More Accurate): Use ADVAN16 [20]. In $DES, code:

3. Saturable Synthesis Implementation:

• Replace constant Kin in the precursor equation with a M-M function: Kin = (VM * Stim) / (KM + Stim), where Stim could be a drug concentration or physiological signal.

4. Estimation:

• Due to model complexity, use the Laplace estimation method (METHOD=4 LAPLACE) or the Stochastic Approximation Expectation-Maximization (SAEM) method available in NONMEM 7.6 [20].

Visualizing Workflows and Model Architecture

Diagram 1: Integrated NONMEM Workflow for Saturable PK/PD Modeling (Max width: 760px)

Diagram 2: Architecture of a Saturable PK/PD Model in NONMEM (Max width: 760px)

The Scientist's Toolkit: Essential Research Reagent Solutions

Table 3: Key Software, Packages, and Model Components

Tool/Component	Category	Primary Function in M-M Research	Reference/Origin
NONMEM 7.6	Primary Software	Gold-standard for nonlinear mixed-effects modeling. Supports SAEM, Bayesian (NUTS), DDEs (ADVAN16/17), and optimal design ($DESIGN).	ICON plc [20]
Automated Initial Estimation Pipeline (R package)	Support Software	Generates robust initial estimates for CL, V, VM, KM from diverse (sparse/rich) datasets, critical for M-M model convergence.	[7]
PREDPP	Subroutine Library	Provides pre-compiled PK models (ADVAN), freeing the user from coding standard differential equations.	Bundled with NONMEM [20]
PsN Toolkit	Support Software	Facilitates model evaluation (VPC, bootstrap), covariate screening, and automation of NONMEM runs.	[55]
$DESIGN Feature	Software Feature	Evaluates and optimizes clinical trial designs via Fisher Information Matrix (FIM) to ensure precise estimation of VM and KM.	NONMEM [54]
Delay Differential Equation (DDE) Solvers (ADVAN16/ADVAN17)	Algorithm	Accurately models biological delays (e.g., enzyme synthesis, cell maturation) impacting saturable processes.	NONMEM 7.6 [53] [20]
Bayesian Estimation (METHOD=BAYES/NUTS)	Algorithm	Incorporates prior knowledge (e.g., in vitro KM) to stabilize estimation, essential for sparse data or complex models.	NONMEM [52] [20]
Surge/Pulse Function	Model Component	Models pulsatile endogenous baseline (e.g., growth hormone) upon which a drug acts on a saturable pathway.	[57]
Transit Compartment Model	Model Component	Approximates a distributed time delay using a series of compartments; simpler alternative to DDEs when variance is small.	[53]
Large Language Models (e.g., Claude 3.5 Sonnet)	AI Assistant	Assists in generating model structure diagrams, summarizing output, and creating report-ready tables from NONMEM results.	[55]

The transition from robust parameter estimation to clinically actionable dosing regimens represents a critical frontier in model-informed drug development. This process is encapsulated by advanced dose optimization algorithms, such as OptiDose, which translate pharmacometric models into individualized dosing strategies [58]. Framed within a broader research thesis on NONMEM for Michaelis-Menten parameter estimation, this document details the application of these concepts. The Michaelis-Menten model, fundamental to characterizing saturable enzymatic elimination (V = Vmax * [S] / (Km + [S])), serves as a cornerstone for parameter estimation, where nonlinear estimation methods (NMs) in NONMEM have demonstrated superior accuracy and precision compared to traditional linearization techniques [24].

The optimization paradigm has evolved from merely identifying the maximum tolerated dose (MTD) to a more nuanced focus on the optimal biological dose (OBD) that balances efficacy and safety [59]. Regulatory initiatives like the FDA's Project Optimus emphasize the need for this reform, particularly in oncology, to ensure doses maximize therapeutic benefit while minimizing adverse effects [60]. The OptiDose algorithm addresses this need by mathematically formulating the dosing challenge as a finite-dimensional optimal control problem (OCP). It computes a dosing regimen (control, u) that minimizes a cost functional (J), measuring the deviation of the system's response from a desired therapeutic target (reference function) [58]. This approach has been enhanced to incorporate state constraints for managing efficacy and safety trade-offs, transforming a constrained OCP into an unconstrained problem solvable within the NONMEM framework [61].

Core Quantitative Findings and Data Synthesis

The reliability of any dose optimization exercise is predicated on the accuracy of the underlying parameter estimates. Comparative studies on Michaelis-Menten parameter estimation provide critical data for informing the initial modeling phase of the OptiDose workflow.

Table 1: Performance Comparison of Michaelis-Menten Parameter Estimation Methods [24]

Estimation Method	Vmax Accuracy (Median Bias)	Vmax Precision (90% CI)	Km Accuracy (Median Bias)	Km Precision (90% CI)	Notes
Nonlinear Methods (NONMEM)	Highest	Narrowest	Highest	Narrowest	Most accurate/precise, especially with combined error models.
Lineweaver-Burk Plot	Low	Wide	Low	Wide	Traditional linearization; prone to error propagation.
Eadie-Hofstee Plot	Low	Wide	Low	Wide	Traditional linearization.
Hanes-Woolf Plot	Moderate	Moderate	Moderate	Moderate	Traditional linearization.
Direct Linear Plot	Moderate	Moderate	Moderate	Moderate	Traditional linearization.

Furthermore, the capabilities of the NONMEM software itself, which is central to implementing OptiDose, have advanced significantly. The latest version, NONMEM 7.6, includes features essential for complex optimization tasks [20].

Table 2: Key NONMEM 7.6 Features Relevant for Dose Optimization [20]

Feature Category	Specific Methods/Algorithms	Utility in Dose Optimization & M-M Research
Population Analysis	FOCE, Laplace, SAEM, IMP, BAYES (NUTS)	Robust estimation of population & individual M-M parameters (Vmax, Km) and their variability.
Advanced Solvers	ADVAN16 (for stiff delay differential equations)	Enables complex PKPD model specification for OptiDose.
Trial Design	Evaluation and optimal design algorithms	Informs efficient sampling for M-M parameter estimation and dose-ranging studies.
Parallel Computing	Multi-core/computer parallelization	Accelerates model estimation, simulation, and optimization runs.

Experimental and Computational Protocols

Protocol 1: NONMEM-based Michaelis-Menten Parameter Estimation fromIn VitroData

This protocol establishes the foundational parameter estimates for saturable elimination pathways [24].

Objective: To accurately estimate Vmax and Km from in vitro drug elimination kinetic data using NONMEM's nonlinear estimation methods.

Materials:

• In vitro incubation data: Substrate concentration ([S]) vs. time profiles from hepatocyte or microsomal incubations.
• Software: NONMEM (v7.6 or later), interface (e.g., Pirana, PsN), R or Python for data preprocessing/post-processing.

Procedure:

• Data Preparation: Structure data in a NONMEM-compatible format (e.g., CSV). Required columns include: ID (experiment identifier), TIME, CONC (substrate concentration), and optionally, a rate column (dCONC/dt).
• Model Specification (Control Stream):
  • Use $PRED or $DES to define the differential equation: dA/dt = - (Vmax * A / (Km + A)) / Volume, where A is the amount.
  • Define initial estimates for THETA(1) (Vmax) and THETA(2) (Km) based on exploratory analysis (e.g., Eadie-Hofstee plot).
  • Specify an appropriate residual error model (e.g., proportional, additive, or combined).
  • Use the SAEM or FOCE estimation method for stability and accuracy [20].
• Model Estimation: Execute the NONMEM control stream. Monitor the minimization and covariance steps for successful completion.
• Model Diagnostics: Evaluate goodness-of-fit: Visual Predictive Check (VPC), individual fits, residual plots. Assess precision of parameter estimates (relative standard error).
• Validation: Perform a bootstrap analysis (e.g., 1000 samples) using PsN to obtain nonparametric confidence intervals for Vmax and Km, verifying robustness.

Protocol 2: Implementing the Enhanced OptiDose Algorithm in NONMEM

This protocol details the translation of a validated PKPD model into an optimized dosing regimen using the enhanced OptiDose method [61].

Objective: To compute an individualized dosing regimen that minimizes a primary efficacy cost function while strictly adhering to a secondary safety constraint.

Materials:

• A finalized population PKPD model with fixed parameters (e.g., from Protocol 1 and subsequent PKPD modeling).
• Software: NONMEM with compiler support, OptiDose algorithm templates [61].

Procedure:

• Problem Formulation:
  • Define State Equation: Code the PKPD model as a system of ODEs in $DES.
  • Define Cost Function (J): Formulate the primary target (e.g., minimize tumor size AUC) [61].
  • Define State Constraint (g(y) ≤ 0): Formulate the safety limit (e.g., neutrophil count N(t) ≥ 1.0 x 10⁹/L) [61].
• Control Stream Configuration:
  • Declare doses (D1, D2,...) as parameters to be estimated (THETA).
  • Implement the penalty method by augmenting the cost function: J_total = J + (ρ/2) * INTEGRAL( max(0, g(y))² ) [61].
  • Use the L-BFGS-B or other constrained optimization algorithm via $ESTIMATION MAXEVALS=9999 METHOD=CONDITIONAL.
• Execution & Iteration:
  • Run NONMEM to solve the unconstrained optimization problem.
  • Check constraint violation. If the constraint is violated, increase the penalty parameter (ρ) and re-run until the solution is feasible.
  • Verify optimality by performing a local sensitivity analysis around the optimal doses.

Protocol 3: High-Performance Computing (HPC) Execution for Large-Scale Optimization

For complex models or population-level optimization, HPC resources are essential [62].

Objective: To efficiently execute computationally intensive NONMEM OptiDose runs using parallel processing on an HPC cluster (e.g., Metworx).

Materials: HPC cluster with SGE/Slurm, NONMEM installed with MPI support, model files.

Procedure:

• Environment Configuration: Configure your session to use compute nodes (e.g., 16-32 vCPU) rather than the head node [62].
• Parallel Job Submission:
  • Using bbr: Submit model with arguments .bbi_args = list(threads=16, parallel=TRUE) [62].
  • Using PsN: Use the -parafile option with a .pnm file specifying NODES=16.
• Performance Tuning: Use empirical testing (e.g., bbr::test_threads()) to identify the optimal number of cores, balancing speed and resource utilization [62].

Visualizing Workflows and Logical Relationships

Diagram 1: PKPD Model Development & OptiDose Optimization Workflow (100 chars)

The Scientist's Toolkit: Essential Research Reagent Solutions

Table 3: Essential Toolkit for M-M Estimation and OptiDose Implementation

Tool / Reagent Category	Specific Item / Software	Function in Research	Key Feature / Note
Primary Modeling Software	NONMEM 7.6 [20]	Gold-standard for NLME PKPD modeling, parameter estimation, and OptiDose algorithm execution.	Includes SAEM, BAYES, advanced solvers (ADVAN16), and parallel computing support.
HPC & Parallelization	Metworx Platform [62]	Cloud-based environment for executing large, parallelized NONMEM jobs efficiently.	Enables configuration of compute nodes matching core counts for optimal parallel speed.
Model Execution Interfaces	bbr R package [62], PsN [62], Pirana [62]	Streamline model submission, management, and execution, especially on HPC clusters.	bbr::test_threads() helps empirically determine optimal core count for parallel runs.
Regulatory & Strategic Framework	FDA Project Optimus Guidance [60]	Provides regulatory framework and expectations for dose optimization in oncology.	Shifts paradigm from MTD to OBD, justifying the need for OptiDose-type approaches.
Model Diagnostics & Evaluation	Nonparametric Estimation (NONP) in NONMEM [26]	Evaluates and identifies non-normal parameter distributions without restrictive assumptions.	Corrects bias from FO method; crucial for accurate variability estimation for simulation.
Advanced Modeling Techniques	Fractional Differential Equation (FDE) Subroutine [17]	Extends NONMEM to model systems with memory/anomalous kinetics using FDEs.	Useful for complex PK where traditional compartment models fail.
Trial Design & Dose Selection	Optimal Biological Dose (OBD) Concept [59]	The target clinical dose that optimally balances efficacy and toxicity.	The clinical endpoint of the OptiDose optimization process.

Solving Convergence Issues and Optimizing Michaelis-Menten Model Performance

Within the context of Michaelis-Menten (MM) parameter estimation using NONMEM, model instability represents a critical barrier to obtaining reliable, reproducible, and biologically plausible estimates of Vmax and Km. Instability is not a singular error but a symptomatic outcome of deeper issues in the interaction between the model structure, the data, and the estimation algorithm [43]. For MM kinetics, which are inherently nonlinear, these issues are often exacerbated. A stable model reliably converges to the same solution with minimal sensitivity to initial estimates, yielding precise parameter uncertainties. An unstable model manifests through failed minimization runs, lack of convergence, biologically implausible parameter estimates (e.g., Vmax approaching infinity), or unreportable standard errors [43]. This document outlines a systematic, practical framework for diagnosing the root causes of instability—focusing on failed minimization and parameter uncertainty—and provides protocols to resolve them, ensuring robust MM parameter estimation.

Core Diagnostic Framework: Symptoms and Root Causes

The first step in diagnosing instability is to categorize the observed symptoms and link them to their most probable underlying causes. This facilitates a targeted investigative approach.

Table 1: Diagnostic Matrix of Model Instability Symptoms and Probable Causes in NONMEM [43]

Symptom Category	Specific NONMEM Manifestations	Associated Probable Causes	Relevance to MM Kinetics
Minimization Failure	Run terminates with error (e.g., rounding error). Failure to converge within iteration limits.	Over-parameterized model relative to data. Poor initial parameter estimates. Extreme correlation between parameters (e.g., Vmax and Km).	High correlation between Vmax and Km is common, especially with limited data spread across the nonlinear curve.
Uncertainty & Reliability	Convergence without standard errors (COVARIANCE STEP OMITTED). Large condition number. Different estimates from different initial values.	Insufficient data information content. "Flat" objective function region near minimum. Unidentifiable parameters.	Data may lack informative points near the Km, making its estimation highly uncertain and the OFV "flat".
Numerical & Performance	Zero gradients during search. Run does not stop (hanging). Poor mixing in Bayesian chains (BAYES).	Poorly scaled parameters (e.g., Km=0.001 vs. Vmax=100). Censored data (BLQ) handling issues [63].	MM parameters often differ by orders of magnitude; improper scaling hinders gradient searches. BLQ data is common in PK.
Biological Implausibility	Theta estimates outside physiological/pharmacological bounds (e.g., negative Km, clearance > cardiac output).	Model misspecification. Data quality issues (outliers, mis-assigned doses). Local minima trap.	May indicate the model is trying to fit noise or that an alternative model (e.g., with parallel linear clearance) is needed.

Detailed Experimental Protocols for Diagnosis and Resolution

The following protocols provide a step-by-step methodology for implementing the diagnostic workflow, specifically tailored for MM model development in NONMEM.

Protocol 1: Systematic Diagnosis of Instability

Objective: To isolate the root cause of minimization failure or excessive parameter uncertainty in a MM model. Workflow: Follow the logic of the diagnostic diagram (Section 5.1).

• Initial Check & Confirmation: Verify the model code accurately represents the intended structural model (e.g., $DES block correctly codes the MM equation dA/dt = - (Vmax * A/V) / (Km + A/V)). Confirm data integrity (doses, concentrations, BLQ markers) [43].
• Evaluate Data Quality & Information Content:
  • Plot observed concentration-time data per individual. For MM elimination, assess if data spans the informative nonlinear region (concentrations around and below Km).
  • Quantify the proportion of BLQ data. Implement and compare different BLQ handling methods (M1, M3, M6+) [63]. The M3 method is precise but can cause instability; the M7+ method (imputing zero with inflated residual error) offers a stable alternative during development [63].
• Profile the Objective Function:
  • Fix the parameter in question (e.g., Km) to a range of values (e.g., from 0.1 to 5 times the estimated value).
  • For each fixed value, estimate all other parameters and record the final Objective Function Value (OFV).
  • Plot OFV vs. parameter value. A flat profile indicates poor data information and unidentifiability. A sharp, well-defined minimum indicates good information but potential for correlation if profiles for Vmax and Km are correlated.
• Assess Parameter Correlation & Scaling:
  • From a successful run, examine the correlation matrix from the covariance step. Correlation between Vmax and Km > |0.95| indicates a problematic, nearly non-identifiable relationship.
  • Check parameter scaling: Initial estimates for parameters should be within a few orders of magnitude of each other. Rescale parameters (e.g., estimate Km in mg/L instead of ng/mL) to improve optimizer performance.

Protocol 2: Generating Robust Initial Estimates for MM Parameters

Objective: To automate the generation of stable initial estimates to prevent minimization failure, using a data-driven pipeline [64]. Background: Poor initial estimates are a primary cause of failed convergence. This protocol adapts a generalized pipeline for use with MM kinetics.

• Data Preparation: Pool data naively (treating all data as from a single subject) based on time after dose (TAD). Bin and calculate median concentrations per time window [64].
• Visual-Guided Estimation (Graphic Method):
  • For IV bolus data with MM elimination, plot log(Concentration) vs. time. The terminal linear phase slope estimates -Vmax/(Km*V). The y-intercept helps estimate V.
  • Use the integrated form of the MM equation to perform nonlinear regression on the pooled data to get initial Vmax and Km estimates.
• Parameter Sweeping for Refinement:
  • Define plausible ranges for Vmax and Km (e.g., Vmax ± 3-fold, Km ± 10-fold from the graphic method estimate).
  • Use a grid search or stochastic search to evaluate multiple (Vmax, Km) pairs. For each pair, simulate the model and compute the relative Root Mean Squared Error (rRMSE) against the pooled median data [64].
  • Select the parameter pair yielding the lowest rRMSE as the robust initial estimate for the population model.

Protocol 3: Resolving Instability via Model Simplification & Re-parameterization

Objective: To stabilize an over-parameterized or poorly identifiable MM model.

• Simplify the Statistical Model:
  • If IIV cannot be reliably estimated on both Vmax and Km, apply IIV to only the more informed parameter (typically Vmax) and fix the other's omega to zero.
  • Simplify the residual error model (e.g., from combined additive+proportional to proportional alone).
• Apply a Stabilizing Re-parameterization:
  • For high correlation between Vmax and Km, re-parameterize the model. Instead of estimating Vmax and Km, estimate Vmax and CLlin, where CLlin = Vmax / Km represents the linear clearance at very low concentrations. The MM equation becomes: Rate = (Vmax * C) / ( (Vmax/CLlin) + C ). This can dramatically reduce correlation.
• Incorporate Prior Information (Bayesian Estimation):
  • If rich prior information on Km or Vmax exists (e.g., from in vitro studies), use the BAYES method in NONMEM with informative priors [20]. This constrains the parameter space and can stabilize estimation.
  • Use the NUTS sampler for improved efficiency on complex models [20].

Table 2: Research Reagent Solutions for Stable NONMEM Modeling [43] [63] [20]

Item Name	Function & Purpose	Key Considerations for MM Models
Automated Initial Estimate Pipeline [64]	An R-based tool to generate data-driven initial estimates for structural and statistical parameters, reducing manual effort and guesswork.	Crucial for MM models to provide starting points that respect the nonlinear saturation curve, preventing early minimization failure.
BLQ Data Handler (M7+ Method) [63]	A pragmatic method for BLQ data: impute zero concentration and inflate the additive residual error for these points. Balances stability with acceptable bias.	Provides a stable alternative to the exact but often unstable M3 method during MM model development, especially with sparse PK data.
Parallel Computing Configuration [62]	Guidelines for configuring NONMEM to run on high-performance computing (HPC) grids (e.g., Metworx) using bbr, PsN, or Pirana with threads=N.	Essential for running complex MM models with large datasets, robust profiling, or Bayesian (BAYES) analysis, which are computationally intensive.
Model Diagnostic Suite (bbr/PsN)	Open-source R package (bbr) and Perl toolkit (PsN) for managing model runs, conducting bootstrap, and performing VPC.	The test_threads() function in bbr helps empirically determine the optimal cores for parallelization, improving efficiency [62].
ADVAN13/ADVAN16 (NONMEM Subroutines) [20]	PREDPP subroutines for solving general nonlinear models (ADVAN13) and stiff delay differential equations (ADVAN16).	ADVAN13 can be used to directly code MM kinetics via differential equations, offering flexibility for complex disposition models.

Visual Guides to the Diagnostic and Resolution Workflow

Diagnostic Decision Pathway for Model Instability

Diagram 1: A logical workflow for diagnosing the root cause of model instability, guiding the user from symptoms to actionable resolution strategies.

Pipeline for Generating Initial Parameter Estimates

Diagram 2: An automated, data-driven pipeline for generating robust initial parameter estimates to ensure stable model start-up [64].

Application Notes

Within the context of advanced pharmacokinetic (PK) research using NONMEM, the Michaelis-Menten (M-M) model is a cornerstone for describing saturable elimination processes (e.g., metabolism via CYP enzymes). A critical challenge is selecting a model that is sufficiently complex to capture the underlying biology without being overparameterized for the available data, which leads to poor parameter identifiability and predictive performance.

Table 1: Model Selection Criteria for Michaelis-Menten Analysis in NONMEM

Criterion	Formula (Approx. in NONMEM)	Interpretation in Context	Optimal Choice
Objective Function Value (OFV)	-2 * Log(Likelihood)	Used for nested model comparison. A drop of >3.84 (χ², p<0.05, 1 df) suggests significant improvement.	Lower is better for nested models.
Akaike Information Criterion (AIC)	OFV + 2 * P	Penalizes for number of parameters (P). Balances fit and complexity for non-nested models.	Lower value indicates better balance.
Bayesian Information Criterion (BIC)	OFV + P * log(N)	Stronger penalty than AIC, dependent on sample size (N). Favors simpler models.	Lower value indicates better balance.
Relative Standard Error (RSE%)	(SE/Estimate)*100	Precision of parameter estimates (Vmax, Km). RSE >30-50% indicates poor identifiability.	Lower RSE indicates higher confidence.
Visual Predictive Check (VPC)	Graphical comparison of observed vs. model-simulated percentiles.	Assesses model's predictive performance across the data range.	Observed percentiles within simulated confidence intervals.

Table 2: Typical Scenarios & Root Causes of Poor Identifiability in M-M Estimation

Scenario	Symptom (in NONMEM Output)	Probable Root Cause	Remedial Action
Sparse data near Km	High RSE for Km, correlation >0.9 between Vmax and Km.	Data information content insufficient to identify the inflection point.	1. Collect richer sampling around expected Km. 2. Consider a simpler linear model if only ascending limb is observed.
High dose saturation	High RSE for Vmax, successful estimation of Km.	Lack of data in the linear, non-saturated range to characterize the maximum rate.	Incorporate lower dose data to define the initial slope.
Complex model on sparse data	Failure to converge, or covariance step omitted.	Model complexity (e.g., + covariates, inter-occasion variability) exceeds data information.	Simplify model hierarchically: remove covariates, then random effects.
Misspecified residual error	Systemic biases in Conditional Weighted Residuals (CWRES) vs. time/prediction.	Error model (e.g., constant CV vs. additive) mis-specified, distorting structural parameter estimates.	Test alternative error models, use extended least squares.

Experimental Protocols

Protocol 1: Base Michaelis-Menten Model Development in NONMEM Objective: To develop a population PK model for a drug exhibiting saturable elimination using NONMEM.

• Data Preparation: Structure dataset with columns: ID, TIME, AMT, DV (observed concentration), EVID (event identifier), RATE for infusion, and relevant covariates (e.g., WT, CYP2D6 phenotype). Ensure doses (AMT) span a range expected to produce both linear and saturated elimination.
• Model Specification:
  • Structural Model: Use the ADVAN13 $DES block or the analytical solution (ADVAN2) to code the M-M equation: dA/dt = - (Vmax * A / (Km + A)) / V, where A is amount in the central compartment, V is volume of distribution.
  • Inter-Individual Variability (IIV): Apply exponential error models to Vmax and Km (e.g., Vmax = TVVMAX * EXP(ETA(1))). Estimate OMEGA matrix.
  • Residual Error Model: Start with a proportional (constant CV) error model: DV = IPRED * (1 + EPS(1)).
• Estimation: Use the First-Order Conditional Estimation (FOCE) with INTERACTION or the more robust Stochastic Approximation Expectation-Maximization (SAEM) method for initial estimates.
• Diagnostics: Generate standard goodness-of-fit plots (Observed vs. Individual/Population Predictions, CWRES vs. TIME/PRED) and evaluate parameter precision (RSE%).

Protocol 2: Stepwise Covariate Model Building on M-M Parameters Objective: To identify significant demographic/pathophysiological covariates on Vmax and Km.

• Base Model: Establish a converged model with IIV on Vmax and Km from Protocol 1.
• Forward Inclusion: a. Graph individual ETA estimates for Vmax and Km vs. potential covariates (e.g., body weight, renal function). b. For each plausible covariate-parameter relationship (linear, power, exponential), add it to the model one at a time. c. Use the Likelihood Ratio Test (LRT): a drop in OFV > 6.64 (χ², p<0.01, 1 df) signifies significance for forward inclusion.
• Backward Elimination: a. After all significant covariates are included, refit the full model. b. Remove each covariate one by one and increase the OFV. Use a stricter criterion (e.g., OFV increase > 10.83, p<0.001) to retain the covariate in the final model.
• Final Evaluation: Perform a Visual Predictive Check (VPC) stratified by key covariates (e.g., renal impairment status) to validate the final model's predictive performance across subpopulations.

Mandatory Visualizations

Title: NONMEM M-M Covariate Model Building Workflow

Title: Data Information vs. Model Complexity Balance

The Scientist's Toolkit: Essential Reagents & Software for M-M NONMEM Analysis

Item	Category	Function/Brief Explanation
NONMEM	Software	Industry-standard software for nonlinear mixed-effects modeling of PK/PD data.
PsN (Perl-speaks-NONMEM)	Software Toolkit	Provides essential utilities for automated model management, bootstrapping, VPC, and cross-validation.
Xpose or Pirana	GUI & Diagnostics	Facilitates model diagnostics, result management, and generation of diagnostic plots.
R or Python	Programming Language	Used for data preparation, post-processing of NONMEM outputs, and custom graphics.
PDx-Pop or Monolix	Alternative Software	Used for model validation or comparison using different estimation algorithms (e.g., SAEM in Monolix).
Rich PK Sampling Strategy	Experimental Design	Data collected across a dose range spanning linear and saturated elimination is crucial for M-M identifiability.
CYP Phenotype/Genuotype Data	Covariate	Key categorical covariate for Vmax in models of drugs metabolized by polymorphic enzymes.
Body Size Metrics (e.g., BSA)	Covariate	Continuous covariate commonly tested on Vmax (allometric scaling) and volume of distribution.

Abstract Within the framework of NONMEM-based Michaelis-Menten parameter estimation research, achieving reliable and computationally stable parameter estimates is a fundamental challenge. This article presents a set of practical methodologies—reparameterization, parameter scaling, and the application of boundary constraints—to address common issues in nonlinear mixed-effects modeling. We provide detailed application notes and experimental protocols, demonstrating how these techniques enhance model identifiability, improve estimation algorithm performance, and ensure the biological plausibility of parameter estimates for maximum reaction rate (Vmax) and Michaelis constant (Km). The protocols are contextualized within the NONMEM 7.6 environment [20] and illustrated using the PREDPP ADVAN10 subroutine, which is explicitly designed for Michaelis-Menten elimination kinetics [19] [36].

The Michaelis-Menten equation is pivotal for modeling saturable metabolic processes in pharmacokinetics. However, estimating its parameters, Vmax and Km, from typical sparse, noisy clinical data presents significant difficulties. The parameters are often highly correlated, and the estimation surface can be flat, leading to poor identifiability, convergence failures, or biologically implausible estimates (e.g., negative values) [24]. These problems are exacerbated in population models where inter-individual variability must be quantified.

This article, framed within a broader thesis on advanced estimation techniques in NONMEM, addresses these challenges through three foundational "practical fixes." The focus is not on introducing novel statistical theory but on providing actionable, detailed protocols for implementing established numerical stabilization techniques within the NONMEM framework. Proper application of these methods is critical for robust population pharmacokinetic-pharmacodynamic (PK/PD) analysis, which forms the basis for model-informed drug development decisions [20] [54].

Reparameterization for Improved Identifiability and Stability

Reparameterization involves rewriting the model's parameterization to create a form that is more amenable to estimation. For the Michaelis-Menten model, this often aims to reduce the correlation between parameters and to define parameters with more orthogonal influences on the objective function.

1.1 Theoretical Foundation The standard Michaelis-Menten equation for elimination rate (V) is: V = (Vmax * C) / (Km + C), where C is the substrate concentration. A common and effective reparameterization is to express the model in terms of intrinsic clearance (CLint) and Vmax, where CLint = Vmax / Km. An alternative parameter, such as Km, is retained. The equation becomes: V = (Vmax * C) / (Km + C) = (CLint * Km * C) / (Km + C). This transformation can help when Vmax and Km are highly correlated, as CLint and Km may have a weaker correlation. Another advanced reparameterization uses a reference concentration (Cref) and the fractional saturation at that concentration to define parameters that are more directly interpretable and better scaled.

1.2 NONMEM Implementation Protocol The following protocol details the implementation of a CLint-reparameterized Michaelis-Menten model using the PREDPP ADVAN10 subroutine.

• Protocol 1.1: Implementing a CLint-Reparameterized Model in NM-TRAN

  • Objective: To specify a one-compartment model with Michaelis-Menten elimination in NONMEM using a CLint and Km parameterization to improve estimation stability.
  • Software: NONMEM 7.6 [20], PREDPP Library (ADVAN10) [19] [36].

  • Control Stream Key Records:

  • Procedure:

    • Prepare a dataset (data.csv) with required columns: ID, TIME, AMT, DV (drug concentration), CMT, EVID, and MDV [19] [65].
    • Implement the control stream as shown. The $PK block defines the typical values (TVCLINT, TVKM), calculates TVVMAX, and applies exponential random effects (ETA) to CLINT and KM.
    • The individual VMAX is derived as the product of individual CLINT and KM.
    • The model parameters VM and KMM are assigned for ADVAN10 [19].
    • Initial estimates for $THETA should be informed by prior knowledge or exploratory analysis [66].
    • Execute the model using a command such as nmfe76 run.ctl run.lst or through an interface like Pirana or Wings for NONMEM [19] [22].
  • Diagnostic & Interpretation: Successful reparameterization often yields a reduced correlation between the estimated ETAs for CLint and Km (visible in the $COVARIANCE output) and more stable convergence. Compare the condition number of the covariance matrix or the correlation matrix of parameter estimates with the standard parameterization to assess improvement.

Table 1: Impact of Reparameterization on Parameter Correlation (Simulated Example)

Parameterization	Estimated Parameter Pair	Correlation Coefficient	Comment
Standard	ETA(Vmax) vs. ETA(Km)	0.95	High correlation, potential identifiability issues.
CLint-based	ETA(CLint) vs. ETA(Km)	0.65	Moderately correlated, improved stability.

Parameter Scaling for Optimized Algorithm Performance

Parameter scaling ensures all parameters subject to estimation have similar orders of magnitude. This is crucial because gradient-based estimation algorithms can fail or become inefficient when parameters differ by several log orders, as is common in PK models (e.g., a Km of 1.2 mg/L vs. a Vmax of 1200 mg/h).

2.1 Principle of Scaling The goal is to transform parameters so their initial estimates and typical values are close to 1 (or within an order of magnitude of 1). This is typically done by dividing the parameter by a scaling constant (e.g., a population typical value or a convenient unit).

2.2 NONMEM Scaling Protocol This protocol integrates scaling directly into the $PK block.

• Protocol 2.1: Implementing Parameter Scaling in the Control Stream

  • Objective: To scale the parameters Km and Vmax to improve the numerical behavior of the estimation algorithm (e.g., FOCE, SAEM).
  • Method: Internal scaling within the control stream.

  • Control Stream Modifications ($PK Block):

  • Procedure:

    • Choose scaling constants (SCALE_xxx) that reflect reasonable prior estimates of the parameters.
    • Define the scaled typical values (TVxxx_SCALED) as THETAs. With initial THETA estimates fixed at 1, the initial biological parameter values equal the scaling constants.
    • In the $THETA record, initial estimates are set to 1. The FIX option can be used during initial testing to ensure the scaling works as intended before allowing estimation.
    • After ensuring the model runs, remove the FIXed status and provide bounded initial estimates around 1 (e.g., (0.5, 1, 5)).
    • The final estimated THETA values are multiplied by the scaling constants to interpret the results in biological units.
  • Diagnostic & Interpretation: Improved algorithm performance is indicated by faster convergence, fewer minimization failures, and more accurate calculation of the covariance matrix. The scaled thetas (close to 1) lead to a better-conditioned Hessian matrix.

Table 2: Example of Parameter Scaling for a Michaelis-Menten Model

Parameter (Biological)	Typical Value	Scaling Constant	Scaled Theta (Initial)	Scaled Theta Bounds
Michaelis Constant (Km)	2.5 mg/L	2.5	THETA(1) = 1.0	(0.1, 1.0, 10.0)
Max. Velocity (Vmax)	50 mg/h	50	THETA(2) = 1.0	(0.2, 1.0, 20.0)

Boundary Constraints to Ensure Biological Plausibility

Boundary constraints prevent parameters from taking on nonsensical values (e.g., negative clearances or volumes) during estimation, which can cause numerical overflow or crash. They incorporate prior knowledge into the estimation.

3.1 Types of Constraints in NONMEM NONMEM allows bounds to be set on $THETA (population parameters) and $OMEGA/$SIGMA$ (variance components). For variance components, a lower bound of a small positive number is common to avoid estimations approaching zero, which can complicate covariance step calculations [67].

3.2 Protocol for Applying Boundaries This protocol combines bounding THETA with the use of the NOABORT option and $ESTIMATION settings for robust estimation.

• Protocol 3.1: Implementing Bounded Estimation for Michaelis-Menten Parameters

  • Objective: To constrain population parameter (THETA) and variance (OMEGA) estimates to biologically plausible ranges and ensure a successful covariance step.

  • Control Stream Modifications:

  • Procedure:

    • Set lower and upper bounds on $THETA using the format (lower, initial, upper). The lower bound for kinetic parameters should always be >0.
    • For variance components ($OMEGA, $SIGMA), a lower bound can be implicitly provided using a positive initial estimate. To set an explicit lower bound, use the format (0.01) for an initial estimate of 0.01 with a lower bound of 0 [67]. The SAME option can be used for variance blocks.
    • Use the NOABORT option in $ESTIMATION to prevent the run from stopping if a numerical error occurs during the covariance calculation, allowing for troubleshooting.
    • The MAXEVAL option prevents indefinite looping.
    • If boundary estimates occur (parameters "pin" at a boundary), this indicates model misspecification, lack of information in the data, or that the bound may be too restrictive.
  • Diagnostic & Interpretation: Check the final parameter estimates in the output file. Parameters hitting a bound will be flagged. Investigate such outcomes by reviewing the data, model structure, or relaxing the bounds if justified. A successful covariance step ($COVARIANCE) with printed standard errors indicates that the estimation was numerically stable near the final estimates.

Integrated Experimental Protocol for Michaelis-Menten Model Development

This protocol integrates the three practical fixes into a coherent workflow for developing a population Michaelis-Menten model, following established model-building stages [66].

• Protocol 4.1: End-to-End Model Development with Practical Fixes
  • Phase 1: Data Preparation and Exploratory Analysis
    • Prepare a NONMEM-formatted dataset [19] [65].
    • Perform graphical check-out using index plots (DV vs. ID, AMT vs. ID) to detect gross errors [66].
    • Obtain naive pooled or individual estimates using simple methods to inform initial scaling constants (SCALE_KM, SCALE_VMAX).
  • Phase 2: Base Model Development
    • Start Simple: Implement a base model using ADVAN10/TRANS1 with a CLint-Km reparameterization (Protocol 1.1).
    • Apply Scaling: Incorporate parameter scaling (Protocol 2.1) using the initial estimates from Phase 1.
    • Apply Constraints: Set liberal but biologically plausible bounds on $THETA and $OMEGA (Protocol 3.1).
    • Initial Estimation: Run with a simple method (e.g., METHOD=CONDITIONAL INTER [67]) to obtain preliminary estimates.
    • Diagnose: Evaluate goodness-of-fit plots (e.g., DV vs. PRED, CWRES vs. TIME) [66].
  • Phase 3: Model Refinement & Final Estimation
    • Refine the statistical model (covariate relationships, variance models) based on diagnostics.
    • Perform final parameter estimation using a more rigorous method (e.g., METHOD=SAEM followed by METHOD=IMP) [20].
    • Execute the final $COVARIANCE step and verify that no parameters are at boundaries and that standard errors are reasonable.
    • Use the $DESIGN feature prospectively to evaluate the expected precision of parameter estimates (e.g., Vmax, Km) for the design used, or retrospectively to understand estimability [54].

The Scientist's Toolkit: Essential Research Reagent Solutions

Table 3: Key Software and Components for NONMEM-based Michaelis-Menten Research

Item	Function / Purpose	Example / Note
NONMEM 7.6	Core engine for nonlinear mixed-effects model estimation [20].	Industry standard software; includes PREDPP and NM-TRAN [20].
PREDPP Library - ADVAN10	Pre-built subroutine for one-compartment models with Michaelis-Menten elimination [19] [36].	Used with $SUBROUTINES. TRANS1 provides the standard VM, KM parameterization [19].
NM-TRAN Control Stream	User-written instruction file specifying the model, parameters, data, estimation methods, and output [65].	A plain text file (.ctl) containing $PROBLEM, $INPUT, $PK, $THETA, etc. [65].
Fortran Compiler	Compiles the NONMEM and user-supplied Fortran code into an executable [20].	Required for installation. Intel Fortran Compiler or gFortran are common [20].
Interface / Wrapper Software	Facilitates run management, model tracking, and graphical diagnostics [19].	Pirana, Perl Speaks NONMEM (PsN), Wings for NONMEM, or R-based tools like xpose [19].
Data File (.csv)	Contains all individual subject data in a structured format for NM-TRAN to read [19] [22].	Required columns include ID, TIME, AMT, DV, EVID, CMT, MDV [19].
Optimal Design Evaluator	Evaluates or optimizes study design using the Fisher Information Matrix (FIM) [54].	NONMEM's $DESIGN record or external tools like PopED and PFIM [54].

Visual Appendix: Workflow and Model Diagrams

Diagram 1: Integrated model-building workflow incorporating the three practical fixes.

Diagram 2: Information flow within the NONMEM system [65].

Diagram 3: Schematic of Michaelis-Menten saturable elimination from a central compartment, as modeled by ADVAN10.

Leveraging Automated Pipelines and Tools for Initial Estimate Generation and Model Search

This document provides detailed application notes and protocols for implementing automated workflows within NONMEM-based research, specifically contextualized within a broader thesis focusing on Michaelis-Menten parameter estimation. Nonlinear mixed-effects (NLME) modeling, the foundation of population pharmacokinetic (PopPK) analysis, is critically dependent on two resource-intensive processes: obtaining robust initial parameter estimates and conducting a thorough search for the optimal model structure. Manual approaches to these tasks are time-consuming, require expert judgment, and can lead to suboptimal models due to local minima or investigator bias [68] [69].

Recent advancements have produced automated pipelines for initial estimate generation that are effective even with sparse data [7] and intelligent global search algorithms that systematically explore vast model spaces [68] [69]. Integrating these tools creates a powerful, standardized framework for pharmacometric analysis. For research centered on Michaelis-Menten kinetics—a system inherently nonlinear and often challenging to fit—leveraging such automation is particularly valuable. It ensures a reproducible, rigorous approach to model development, allowing the researcher to focus on the biological interpretation of the saturated enzymatic process rather than the intricacies of model tuning and search logistics.

Automated Pipeline for Initial Estimate Generation

The generation of high-quality initial estimates is a prerequisite for successful and efficient model convergence in NONMEM. An automated, data-driven pipeline has been developed to replace manual methods like non-compartmental analysis (NCA), which struggles with sparse data [7].

Pipeline Architecture and Workflow

The pipeline is designed to process data formatted to nlmixr2 standards and proceeds through three consecutive parts to compute initial estimates for structural and statistical parameters [7].

Diagram 1: Architecture of the automated initial estimate pipeline [7].

Core Methodologies and Protocols

Protocol 2.2.1: Data Preparation and Naïve Pooling

• Objective: To standardize raw data and create pooled concentration-time profiles for population-level analysis.
• Steps:
  • Assign Dosing Information: Process observation records to assign dosing events, identify administration routes (IV bolus, infusion, extravascular), and calculate time after the last dose (TAD).
  • Categorize Data: Separate data into three groups: first-dose, non-first-dose (multiple-dose), and mixed-dose data.
  • Pool and Bin: For each group, bin concentration-time data based on TAD. Use a default of 10 time windows (adjusting if fewer unique time points exist) to ensure adequate PK curve characterization.
  • Calculate Representative Values: Within each time window, compute the median time and median drug concentration. These paired medians form the pooled concentration-time profile used in subsequent steps [7].

Protocol 2.2.2: Adaptive Single-Point Method

• Objective: To estimate clearance (CL) and volume of distribution (Vd) from datasets with sparse sampling (e.g., one sample per individual).
• Base Phase Protocol:
  • Estimate Half-life: Perform linear regression on the terminal phase of the naïve pooled data to estimate elimination rate constant (λz) and half-life (t₁/₂).
  • Calculate Vd: For intravenous data, identify the first concentration (C₁) sampled within 0.2*t₁/₂ after a first dose. Approximate Vd as Dose / C₁.
  • Calculate CL: Under steady-state conditions (achieved after ≥5 doses), identify maximum (Cˢˢmax) and minimum (Cˢˢmin) concentrations within a dosing interval (τ). Calculate average concentration (Cˢˢavg). Compute CL as Dose / (Cˢˢavg * τ).
  • Summarize Population Estimates: Calculate the geometric mean (with a 5% trim) of individual parameter estimates to derive robust population initial values [7].

Protocol 2.2.3: Parameter Sweeping for Complex Models

• Objective: To find initial estimates for parameters in complex models (e.g., Michaelis-Menten elimination, multi-compartment distribution) where direct calculation is not feasible.
• Steps:
  • Define Search Range: Establish a biologically plausible range for the parameter in question (e.g., Vmax, Km).
  • Generate Candidates: Create a vector of candidate values spanning the defined range.
  • Simulate and Compare: For each candidate value, simulate the model and predict concentrations. Hold other parameters constant at preliminary estimates.
  • Evaluate Fit: Calculate the relative Root Mean Squared Error (rRMSE) between the observed data (or pooled profile) and the predictions for each candidate.
  • Select Best Estimate: Choose the candidate parameter value that yields the lowest rRMSE as the initial estimate [7].

Performance and Validation Data

The pipeline was rigorously validated using simulated and real-world datasets.

Table 1: Validation Performance of the Automated Initial Estimate Pipeline [7]

Dataset Type	Number of Datasets	Performance Outcome	Key Metric
Simulated	21	Final parameter estimates were closely aligned with pre-set true values.	Successful convergence with accurate final estimates.
Real-Life	13	Final parameter estimates were closely aligned with established literature references for the drugs.	Production of biologically plausible, literature-backed models.
Overall	34	The pipeline performed well in all test cases for both rich and sparse data scenarios.	100% success rate in providing usable initial estimates.

Automated Tools for Population Model Search

Once a base model is initialized, identifying the optimal structural and covariate model is the next challenge. Automated global search algorithms overcome the limitations of traditional stepwise "hill-climbing" methods, which are prone to local minima [68].

Search Algorithm Theory and Implementation

Local vs. Global Search: Traditional stepwise addition/backward elimination is a local search "greedy algorithm." It evaluates models close to the current best model and moves in the direction of immediate improvement. Its success depends entirely on starting in a region "convex" to the global optimum, an assumption often false in complex PK/PD model spaces [68].

Global search algorithms evaluate models that may be very different from each other, allowing them to escape local minima. Key algorithms include:

• Genetic Algorithms (GA): Mimic natural selection. A population of models (individuals) undergoes selection, crossover (mating), and mutation over generations to evolve towards better fit [68].
• Gene Expression Programming (GEP): An extension of GA that evolves complex mathematical expressions or model structures, useful for discovering non-polynomial covariate relationships [70].
• Bayesian Optimization with Surrogate Models: Uses a probabilistic model (e.g., random forest) to predict the performance of untested models, guiding the search efficiently towards promising regions of the vast model space [69].

Diagram 2: Workflow of a genetic algorithm for automated model search [68] [69].

Integrated Protocol: Automated Model Search with pyDarwin

Protocol 3.2.1: Setup and Pre-processing

• Objective: To configure an automated model search for a PopPK dataset, such as one featuring Michaelis-Menten elimination.
• Tools: pyDarwin (optimization library), NONMEM as the estimation engine [69].
• Steps:
  • Data Formatting: Ensure the dataset is formatted for NONMEM, including necessary covariates.
  • Define Model Search Space: Specify the universe of possible models. For extravascular drugs, this may include:
    • Compartments: 1- or 2-compartment distribution.
    • Absorption Models: First-order, zero-order, parallel, or transit compartments.
    • Elimination Models: Linear, Michaelis-Menten, or combined.
    • Covariate Relationships: Potential continuous or categorical covariates on parameters (e.g., weight on Vd, age on CL).
  • Specify Penalty Function: Define an objective function that balances goodness-of-fit with model plausibility. A recommended composite penalty includes:
    • Akaike Information Criterion (AIC): Penalizes model complexity to avoid overfitting.
    • Parameter Plausibility Term: Penalizes abnormal parameter values (e.g., very high/low inter-individual variability, high shrinkage, unrealistic volume estimates) [69].

Protocol 3.2.2: Execution of the Global Search

• Objective: To efficiently explore the pre-defined model space and identify the optimal structure.
• Steps:
  • Initialization: pyDarwin generates an initial population of random model structures from the search space.
  • Iterative Evaluation Loop: a. Fitness Evaluation: Each model in the population is run in NONMEM (or a surrogate evaluates its expected performance). The composite penalty function score is calculated. b. Selection & Evolution: Algorithms like GA or Bayesian Optimization select the fittest models, apply genetic operators (crossover, mutation) or probabilistic inference to propose a new, promising generation of models.
  • Convergence: The search continues for a set number of generations or until the improvement in the best fitness score falls below a threshold.
  • Output: The model with the optimal (lowest) penalty function score is selected as the final, recommended model structure [69].

Performance Data and Comparison

Table 2: Performance of Automated Model Search (pyDarwin) vs. Manual Development [69]

Metric	Automated Search (pyDarwin)	Traditional Manual Search
Average Development Time	Less than 48 hours (in a 40-CPU, 40 GB RAM environment).	Often several days to weeks, depending on model complexity and analyst workload.
Search Efficiency	Evaluated fewer than 2.6% of the total models in a >12,000-model search space.	Typically explores a minuscule fraction of the possible model space due to time constraints.
Risk of Local Minima	Low. Global search algorithms (GA, Bayesian Optimization) are designed to escape local minima.	High. Stepwise "hill-climbing" is intrinsically susceptible to local minima [68].
Reproducibility	High. The search is defined by an explicit, code-based penalty function and search space.	Variable. Depends on analyst expertise and subjective judgment, leading to potential irreproducibility [69].
Model Quality Outcome	Identified model structures were comparable or very close to manually developed expert models for clinical datasets [69].	Dependent on the skill and experience of the modeler; can be optimal but consistency is not guaranteed.

The Scientist's Toolkit: Essential Research Reagents & Software

Table 3: Key Software Tools and Methodological Components for Automated NONMEM Workflows

Tool/Component	Primary Function	Role in Automated Workflow	Source/Reference
NONMEM 7.6	Industry-standard software for NLME population PK/PD analysis. Provides multiple estimation methods (FOCE, SAEM, IMP, BAYES).	Core estimation engine. All automated pipelines ultimately execute candidate models here for parameter estimation and objective function calculation.	[20] [32]
R Package for Initial Estimates	Open-source R package implementing the automated pipeline (data prep, single-point, NCA, graphic methods, sweeping).	Provides the initial estimates for THETAs (structural parameters) required to start model estimation, crucial for complex models like Michaelis-Menten.	[7] [71]
pyDarwin	A Python library for global optimization. Implements genetic algorithms, Bayesian optimization, and other search strategies.	Orchestrates the automated model search. It generates candidate model structures, manages their evaluation (often via NONMEM), and evolves the population.	[69]
nlmixr2	An R package for NLME modeling that provides a unified interface and facilitates model specification and simulation.	Serves as a data standard and potential alternative/supplementary estimation environment. The initial estimate pipeline uses its data format [7].	[7]
Composite Penalty Function	A user-defined function combining AIC (for complexity) and parameter plausibility checks (for biological realism).	Guides the automated model search by objectively scoring and ranking candidate models, replacing subjective analyst judgment during model selection [69].	[69]
Gene Expression Programming (GEP)	An evolutionary algorithm specialized for discovering symbolic mathematical relationships.	Useful for automated covariate model building, particularly for identifying non-linear or non-polynomial covariate-parameter relationships [70].	[70]
Perl-speaks-NONMEM (PsN)	A versatile toolkit of Perl scripts for facilitating NONMEM modeling, including automated stepwise covariate analysis (SCM).	Represents an earlier generation of automation tools, primarily for covariate selection. Useful for specific, well-defined sub-tasks [72].	[72]

Within the domain of pharmacometrics and model-informed drug development, constructing robust nonlinear mixed-effects (NLME) models is fundamental. For research focused on Michaelis-Menten (M-M) parameter estimation using NONMEM, stability—defined as a model's reliable convergence to consistent and biologically plausible parameter estimates—is a critical yet frequently elusive goal [43]. Instability manifests as failed minimization, absence of standard errors, or parameter estimates that shift dramatically with minor changes in initial values or estimation algorithms [43] [32]. This undermines the reliability of key parameters like Vmax (maximum elimination rate) and Km (Michaelis constant), which are crucial for predicting nonlinear pharmacokinetics and dose-concentration relationships.

The root causes of instability are often multifaceted, arising from the intricate interplay between model complexity, data information content, and data quality [43]. An inherently complex M-M model may exceed what the available data can inform, leading to poorly identifiable parameters. Concurrently, common practices like suboptimal initial parameter estimates can trap estimation algorithms in local minima or cause premature termination [7]. This article presents a structured, heuristic workflow to diagnose and resolve these stability issues, framed explicitly within the context of advancing NONMEM-based M-M pharmacometric research.

Diagnostic and Resolution Workflow for Model Stability

The following workflow provides a systematic, step-by-step approach for diagnosing the root cause of instability and implementing targeted corrective actions. It synthesizes a problem-solving heuristic [43] with foundational principles of NONMEM estimation [32] [19] and modern automated techniques for initial estimation [7].

Diagram 1: Heuristic Workflow for Diagnosing and Resolving Model Instability (94 characters)

Detailed Experimental Protocols & Application Notes

Protocol 1: Generating Robust Initial Parameter Estimates for M-M Models

Poor initial estimates are a primary cause of convergence failure [7]. This protocol details an automated, data-driven pipeline to generate reliable starting values for M-M parameters (Vmax, Km), volumes (V), and residual error, applicable to both rich and sparse data scenarios.

• Data Preparation: Format the dataset with required columns: ID, TIME, AMT, DV (observed concentration), EVID (event identifier), and CMT (compartment number). Prepare a naïve pooled dataset by binning concentration-time data from all subjects based on time-after-dose windows and calculating median values for each window [7].
• Estimation for One-Compartment Linear Proxy:
  • Use the pooled data to estimate a linear one-compartment model with first-order elimination (CL, V) as an initial proxy. Employ an adaptive single-point method: Calculate apparent clearance (CL) at steady state using the average of maximum and minimum concentrations (Css,avg) and the dosing interval (τ): CL = Dose / (Css,avg * τ). Estimate volume (V) from the first post-dose concentration, provided it is sampled early (within ~20% of the estimated half-life) [7].
  • Alternatively, apply graphic methods (e.g., terminal slope regression for intravenous data) or naïve pooled Non-Compartmental Analysis (NCA) to the median pooled profile to obtain CL and V estimates [7].
• Initializing M-M Parameters (Vmax & Km):
  • Use the CL estimate from Step 2 as an approximation of the linear clearance at low concentrations. Set the initial Km to a value roughly in the middle of the observed concentration range.
  • Employ parameter sweeping: Define a plausible range for Vmax (e.g., 0.5 to 2 times the dose/hour) and Km (e.g., 0.1 to 10 times the median concentration). Simulate the M-M model across a grid of these values using the pooled data structure. Select the (Vmax, Km) pair that minimizes the relative Root Mean Square Error (rRMSE) between simulated and median observed concentrations [7].
• Initializing Statistical Parameters:
  • For inter-individual variability (IIV, OMEGA), set pragmatic diagonal elements (e.g., 0.09 for 30% coefficient of variation) for CL, V, Vmax, and Km [7].
  • For residual unexplained variability (RUV, SIGMA), use a data-driven estimate from the variance of the pooled profile or a fixed default (e.g., additive error of 10% of the median observation) [7].

Protocol 2: Diagnostic Evaluation of Model Stability

After obtaining initial estimates, run a simplified "restricted" model (e.g., M-M elimination only, no covariates, diagonal OMEGA) with a robust estimation method like FOCE or IMP [32]. Analyze these key diagnostics to pinpoint instability [43]:

• Condition Number & R Matrix: In NONMEM output, examine the eigenvalues of the correlation matrix (R matrix). Calculate the condition number (ratio of largest to smallest eigenvalue). A condition number > 1000 indicates severe ill-conditioning and parameter non-identifiability [43].
• Standard Error Reliability: Check for successful calculation of standard errors (SE) for all parameters. Parameters with extremely large relative SE (>50%) or a failure to compute SEs indicate poor practical identifiability.
• Objective Function Value (OFV) Stability: Run the model multiple times from different starting points (perturbed by ±10-20%). A stable model will converge to a nearly identical OFV; unstable models will yield different OFVs or fail.

Protocol 3: Parameterization & Estimation Strategies for M-M Models

Based on the diagnostics, apply targeted corrections:

• For High Condition Number/Ill-Conditioning: Reparameterize the model. For a one-compartment M-M model, use the standard clearance (CL) and volume (V) parameterization (ADVAN10 TRANS2 in NONMEM) instead of micro-constants (ADVAN10 TRANS1) [19]. If Km is poorly identifiable, consider fixing it to a literature value from in vitro studies or simplifying the model to linear elimination if supported by the data [43].
• For Unreliable Standard Errors or Run Failures: Switch the estimation algorithm. Move from a linearization method (FOCE) to a sampling-based method like Importance Sampling (IMP) or Stochastic Approximation EM (SAEM), which are more robust for nonlinear models and can provide better uncertainty estimates [32]. For complex models defined by ordinary differential equations (ODEs), ensure the appropriate ODE solver (ADVAN13, ADVAN14) is specified [19].
• Iterative Model Simplification: If instability persists, systematically reduce model complexity. This may involve fixing IIV on less variable parameters (e.g., Km), switching from a full to a diagonal OMEGA block, or using a simpler residual error model.

Data Presentation: Comparative Analysis of Methods

Table 1: Performance of Estimation Methods for Nonlinear Models (e.g., M-M) [32] [13]

Estimation Method	Key Principle	Computational Speed	Robustness for M-M	Best Use Case in Stability Workflow
FO (First Order)	Linearizes inter & intra-individual variability.	Very Fast	Low (biased for nonlinearity)	Not recommended for M-M models.
FOCE (First Order Conditional Estimation)	More accurate approximation than FO.	Fast	Moderate	Initial diagnostic runs with good initial estimates.
IMP (Importance Sampling)	Monte Carlo integration in "important" parameter region.	Slow	High	Final estimation after stabilization; obtains reliable standard errors.
SAEM (Stochastic Approximation EM)	Markov Chain Monte Carlo (MCMC) sampling.	Slow (but efficient for ODEs)	High	Complex models where FOCE fails; often requires final IMP step for covariance.
Nonlinear Regression (Pooled Data)	Fits naïve pooled data ignoring IIV.	Very Fast	Medium (for initial estimates)	Protocol 1: Generating initial Vmax and Km estimates.

Table 2: Common Stability Diagnostics and Interpretations [43]

Diagnostic Metric	Acceptable Range	Indication of Instability	Suggested Corrective Action
Condition Number	< 1000	> 1000 indicates ill-conditioning.	Reparameterize model; fix correlated parameters.
Relative Standard Error (RSE)	< 30-50% for key parameters	RSE > 50% or "NaN".	Simplify model; switch to IMP/SAEM method [32].
OFV Variation from Different Starts	∆OFV < 0.1	∆OFV > 2.0.	Improve initial estimates (use Protocol 1).
Minimization Status	"MINIMIZATION SUCCESSFUL"	"MINIMIZATION TERMINATED".	Check data quality/outliers; review model code for errors.

Table 3: Recommended Parameterization for M-M Models in NONMEM [19]

Model Feature	Problematic Parameterization	Recommended Stable Parameterization	Rationale
Structural Model	Micro-rate constants (ADVAN10 TRANS1: K, V).	Clearance/Volume (ADVAN10 TRANS2: CL, V).	Reduces parameter correlation; more intuitive.
M-M Parameters	IIV on both Vmax and Km.	IIV only on Vmax (or CL); fix Km or assign low IIV.	Km is often poorly identifiable; reduces complexity.
Statistical Model	Full OMEGA block for CL & V.	Diagonal OMEGA matrix.	Avoids estimating covariance, improving stability.
Residual Error	Complex combined error early on.	Simple additive or proportional error.	Fewer parameters to estimate during stabilization.

The Scientist's Toolkit: Essential Research Reagents & Solutions

Table 4: Key Software Tools and Methodological "Reagents" for Stability Resolution

Tool / Method	Category	Primary Function in Stability Workflow	Reference / Source
NONMEM (with PREDPP)	Core Software	Industry-standard engine for NLME model fitting and simulation.	[19]
nlmixr2autoinit R package	Automation Tool	Implements Protocol 1 for automated, data-driven generation of initial parameter estimates.	[7] [73]
IMP & SAEM Algorithms	Estimation Method	Robust, sampling-based estimation methods for unstable models or obtaining reliable covariance (Protocol 3).	[32]
Condition Number & R-matrix	Diagnostic Metric	Key numerical diagnostic for identifying parameter non-identifiability and ill-conditioning.	[43]
Naïve Pooled Data Analysis	Modeling Technique	Creates a median profile for graphic methods/NCA to inform initial estimates for complex models.	[7]
Model Reparameterization	Modeling Strategy	Technique to reduce parameter correlation (e.g., using CL instead of K) to improve conditioning.	[43] [19]
Perl-speaks-NONMEM (PsN)/Pirana	Run Management	Facilitates efficient model execution, diagnostic scripting, and workflow management.	[74]

Validating Model Predictions and Comparing NONMEM with Emerging AI/ML Methodologies

Visual Predictive Checks (VPC) and numerical metrics are cornerstone techniques for validating nonlinear mixed-effects models (NLMEMs), particularly in the context of Michaelis-Menten (MM) pharmacokinetic models estimated using NONMEM. Within a thesis focused on MM parameter estimation, these diagnostics are essential for assessing whether a model can adequately describe observed data and for detecting structural or stochastic model misspecification [75] [76]. A VPC works by comparing key percentiles (e.g., 10th, 50th, 90th) of observed data against prediction intervals derived from hundreds or thousands of simulated datasets generated from the candidate model [75] [76]. This graphical check evaluates if the model can reproduce the central tendency and variability of the observations. For MM models, which are inherently nonlinear and can present identifiability challenges, VPCs are complemented by numerical metrics to provide a robust, multi-faceted assessment of model performance and reliability [16].

Visual Predictive Check Methodologies and Protocols

Core VPC Workflow and Protocol

The generation of a standard VPC follows a defined sequence of simulation, binning, and comparison.

VPC Generation and Assessment Workflow

Protocol 2.1.1: Standard VPC Generation for an MM Model

• Model Simulation: Using the final estimated MM model parameters, simulate 500-1000 replicate datasets in NONMEM using the $SIMULATION block or a tool like PsN. Each replicate must match the original study design (doses, sample times, covariates) [77] [76].
• Data Binning: For both observed and simulated data, group observations into intervals (bins) of the independent variable (typically time). The number of bins (e.g., 8-10) is a trade-off; too few lose detail, too many create noisy percentiles [75]. Bins can be defined by equal time intervals, equal number of observations, or automated methods (e.g., Jenks) [75] [78].
• Percentile Calculation: Within each bin, calculate the desired percentiles (e.g., 10th, 50th, 90th) for the observed data. For the simulated data, calculate the same percentiles for each individual replicate.
• Prediction Interval (PI) Calculation: From the collection of simulated percentiles across all replicates, calculate the median and a prediction interval (e.g., the 5th to 95th percentile) for each percentile line (e.g., the 90% PI for the simulated 50th percentile) [77].
• Plotting and Assessment: Generate the VPC plot. The x-axis is typically the independent variable (time), and the y-axis is the dependent variable (e.g., concentration). The plot displays:
  • Shaded areas representing the simulated prediction intervals for each percentile.
  • Solid lines representing the median of the simulated percentiles.
  • Symbols or dashed lines representing the observed percentiles. A model is considered adequate if the observed percentiles generally fall within the corresponding simulated prediction intervals [75] [76].

Advanced VPC Techniques

For complex MM models or heterogeneous study designs, standard VPCs can be misleading. Advanced correction techniques are required.

Prediction-Corrected VPC (pcVPC): This method corrects for variation in population predictions (PRED) across bins, which is crucial when doses or covariates vary widely. It normalizes observed (DV) and simulated data using the formula: pcY = Y * (median(PRED_bin) / PRED_ind) [77] [75]. This removes the confounding effect of the independent variable, allowing for a clearer diagnosis of model misfit.

Regression-Based VPC: This approach eliminates the subjective and sometimes problematic step of binning. It uses Additive Quantile Regression (AQR) to smoothly estimate percentiles for observed and simulated data over the independent variable, and LOESS regression to calculate the expected population prediction for pcVPC [79]. This method is particularly useful for sparse or irregularly sampled data.

Reference-Corrected VPC (rcVPC): A recent advancement, the rcVPC addresses the unintuitive y-axis scaling of pcVPC plots. It normalizes observations and simulations by the population prediction from a user-defined reference scenario (e.g., a standard dose), making trends directly interpretable in the original units and facilitating communication of exposure-response relationships [80].

Table 2.2.1: Comparison of VPC Techniques for MM Model Validation

VPC Type	Key Principle	Primary Use Case	Advantages	Key Considerations
Standard VPC	Compares binned percentiles of observed vs. simulated data.	Homogeneous study designs with consistent dosing and sampling.	Intuitive, simple to implement and explain.	Misleading with variable dosing/covariates. Binning strategy affects results.
Prediction-Corrected VPC (pcVPC)	Normalizes data by typical population prediction per bin [77] [75].	Heterogeneous designs (varying doses, strong covariates).	Removes bias from design variability, more accurate diagnosis.	Y-axis values are normalized and less intuitive [80].
Regression-Based VPC	Uses quantile regression (AQR) instead of binning [79].	Sparse, irregular data where binning is problematic.	Eliminates binning bias, provides smooth percentile estimates.	Computationally more intensive, requires selection of smoothing parameters.
Reference-Corrected VPC (rcVPC)	Normalizes data by predictions from a user-defined reference scenario [80].	Communicating model performance, exploring exposure-response.	Y-axis in original units, highly intuitive, good for communication.	Requires definition of an appropriate reference scenario.

Decision Logic for Selecting VPC Technique

Practical Implementation Protocol

Protocol 2.3.1: Implementing a pcVPC using NONMEM/PsN and R/xpose This protocol is central to a thesis on MM model validation [77] [78].

• Simulation with PsN: Execute the PsN vpc command with the -predcorr argument to ensure the population prediction (PRED) column is included in the simulation output. Specify the number of replicates (e.g., -samples=500). This can also be done within NONMEM's control stream using $SIMULATION.

• Data Processing in R: Use the xpose package to read the simulation output.

• Generate pcVPC: Use the vpc_data() and vpc() functions, specifying vpc_type = 'continuous'. The predcorr option is automatically handled if the PsN run included -predcorr.

• Stratification: If the model includes categorical covariates (e.g., genotype affecting Vmax), use the stratify argument to create separate VPC panels for each subgroup, ensuring the model fits all subpopulations adequately [78] [76].

Numerical Validation Metrics for Michaelis-Menten Models

While VPCs provide a powerful visual diagnostic, numerical metrics are critical for objective assessment, especially for complex MM models where parameter identifiability can be an issue [16].

Parameter Estimation Diagnostics

Table 3.1.1: Key Numerical Metrics for MM Model Validation

Metric Category	Specific Metric	Interpretation for MM Models	Target/Threshold
Precision of Estimates	Relative Standard Error (RSE%)	RSE% = (SE/Estimate)*100. High RSE% (>30-50%) for Vmax or Km suggests poor identifiability [16].	< 30% (ideal), < 50% (acceptable)
Model Convergence	NONMEM Termination Status	Successful covariance step (MINIMIZATION SUCCESSFUL, COVARIANCE STEP PASSED).	Required.
	Significant Digits (SIGDIG)	A measure of estimation precision. SIGDIG=3 is traditional but may be insufficient for nonlinear models; ≥4-6 is more robust [81].	≥ 4
Goodness-of-Fit (GOF)	Objective Function Value (OFV)	Used for hypothesis testing between nested models (ΔOFV). Lower is better.	ΔOFV > -3.84 (p<0.05) for 1 parameter difference.
	Condition Number	Ratio of largest to smallest eigenvalue of the correlation matrix. Indicates collinearity (e.g., between Vmax and Km).	< 1000
Simulation-Based	Normalized Prediction Distribution Errors (NPDE)	A statistical test comparing the entire distribution of observations to simulations. Can detect misfit not visible in VPC percentiles.	Mean ≈ 0, Variance ≈ 1, p-value of tests > 0.05

Protocol for Assessing Identifiability and Robustness

MM parameters (Vmax, Km) can be statistically non-identifiable, meaning different parameter pairs can fit the data equally well [16].

Protocol 3.2.1: Identifiability and Stability Check

• Profile Likelihood Analysis:
  • Fix one MM parameter (e.g., Km) to a range of values around the estimate.
  • Re-estimate all other model parameters and record the OFV for each fixed value.
  • Plot OFV vs. the fixed parameter value. A sharp, V-shaped trough indicates good identifiability. A flat or shallow trough suggests poor identifiability.
• Bootstrap Analysis:
  • Perform non-parametric bootstrap (e.g., 1000 resamples) to generate a distribution of parameter estimates.
  • Calculate the median and 95% confidence intervals from the bootstrap distributions for Vmax and Km.
  • Compare the original estimates to the bootstrap medians and CIs. Large shifts or very wide CIs indicate instability and potential identifiability problems.
• Global Optimization Verification: To rule out convergence to a local minimum—a known risk with derivative-based methods like FOCE in NONMEM—use a global optimization algorithm as a verification step [16]. Tools like Particle Swarm Optimization (PSO) or its variants (LPSO) can be applied. If PSO finds a significantly lower OFV than NONMEM's FOCE/SAEM, the original solution is likely a local minimum, and estimation should be restarted with different initial estimates [16].

The Scientist's Toolkit for MM Model Validation

Table 4.1: Essential Software and Research Reagent Solutions

Tool/Reagent	Category	Primary Function in Validation	Application Note
NONMEM	Core Estimation Software	Estimates population parameters (THETA, OMEGA, SIGMA) for MM models using FOCE, SAEM, or IMP methods [32].	The workhorse for NLMEM estimation. Outputs model files and simulations for diagnostics.
Perl Speaks NONMEM (PsN)	Toolkit / Wrapper	Automates complex tasks: VPC simulation, bootstrap, model comparison [77] [78].	Essential for running standardized, reproducible validation workflows.
R Statistical Environment	Data Analysis & Visualization	Data manipulation, statistical calculation, and generation of diagnostic plots (GOF, VPC) [77] [79] [78].	The flexible, open-source platform for custom analysis and graphics.
xpose R Package	Dedicated Diagnostics Package	Specialized for reading NONMEM output and creating pharmacometric diagnostics, including VPCs [78] [82].	Streamlines the creation of publication-quality VPC and GOF plots.
Monolix Suite	Alternative Software	Performs NLMEM estimation and provides integrated, advanced VPC features for various data types [75].	Useful for cross-verification of NONMEM results and its VPC interface is user-friendly.
Particle Swarm Optimization (PSO) Code	Global Optimization Algorithm	Verifies that NONMEM estimates represent a global, not local, minimum of the objective function [16].	Critical final check for MM models prone to identifiability issues. Custom or published code (e.g., LPSO) is required.
High-Performance Computing (HPC) Cluster	Computational Resource	Provides the necessary power to run large simulation tasks (1000+ VPC replicates, bootstrap).	Enables thorough validation within practical timeframes for complex models.

Within pharmacometrics, Model-Informed Drug Development (MIDD) leverages mathematical models to optimize drug development and dosing strategies [83]. For decades, nonlinear mixed-effects modeling (NLMEM) implemented in software like NONMEM has been the gold standard for population pharmacokinetic (PPK) analysis, including the estimation of Michaelis-Menten (MM) parameters that characterize saturable metabolic or transport processes [83] [32]. These traditional methods are built on mechanistic principles, offering interpretability and regulatory familiarity.

The emergence of artificial intelligence and machine learning (AI/ML) presents a paradigm shift, promising enhancements in predictive accuracy, computational efficiency, and the ability to handle complex, high-dimensional data [83] [84]. This application note provides a structured, evidence-based comparison between traditional NONMEM MM models and contemporary AI/ML predictors. Framed within broader thesis research on MM parameter estimation, it details experimental protocols, quantitative benchmarks, and practical workflows to guide researchers and drug development professionals in evaluating and integrating these complementary methodologies.

Quantitative Performance Benchmarking

A direct comparative analysis reveals the relative strengths and performance characteristics of traditional and AI/ML approaches under different conditions.

Table 1: Performance Comparison of NONMEM vs. AI/ML Models in PPK Analysis

Model Category	Specific Model/Approach	Key Performance Metric (RMSE/MAE)	Computational Time	Key Strength	Primary Data Context	Source
Traditional NLMEM	NONMEM (FOCE, SAEM)	Baseline Reference	Variable (hrs-days)	Interpretability, Regulatory Acceptance	Real (n=1,770) & Simulated	[83] [32]
Machine Learning (ML)	XGBoost, Random Forest	Often outperformed NONMEM	Minutes-Hours	Handling non-linear covariate relationships	Real Clinical Datasets	[83] [84]
Deep Learning (DL)	Neural Networks (NN)	Often outperformed NONMEM	Moderate-High (GPU-dependent)	Pattern recognition in complex data	Large Real Clinical Datasets	[83]
Hybrid AI-NLMEM	Neural Ordinary Differential Equations (Neural ODE)	Strong performance, high explainability	High	Mechanistic + Data-driven fusion	Large Datasets	[83]
Automated PPK Search	pyDarwin (Bayesian Optimization)	Comparable to expert manual models	< 48 hours (avg., 40-CPU)	Exhaustive search, reproducibility	Synthetic & Real Clinical Datasets	[69]

Interpretation of Benchmarks: The data indicates that AI/ML models, particularly neural ODEs and automated search algorithms, can match or exceed the predictive accuracy of traditional NONMEM models [83] [69]. A pivotal 2025 comparative study on real-world data from 1,770 patients found that AI/ML models "often outperform NONMEM," with neural ODEs providing a strong balance of performance and explainability [83]. Furthermore, automated AI-driven platforms can reliably identify optimal model structures in a fraction of the time required for manual development, significantly accelerating the popPK analysis timeline [69].

Detailed Experimental Protocols

Protocol 1: Traditional NONMEM Workflow for MM Parameter Estimation

This protocol outlines the established, iterative process for developing a population MM model using NONMEM.

• Model Specification:

  • Define the structural base model using the MM equation: ( dA/dt = -V{max} \cdot C / (Km + C) ), where ( V{max} ) is the maximum rate and ( Km }) is the substrate concentration at half-maximal velocity.
  • Specify the statistical model for inter-individual variability (IIV) on parameters (e.g., exponential error model for ( V{max} ) and ( Km )), covariance (OMEGA matrix), and residual error model (SIGMA).

• Parameter Estimation:

  • Algorithm Selection: Choose an estimation method based on model complexity and data [32].
    • FOCE with INTERACTION: Recommended for most PK/PD models, including MM, with moderate nonlinearity.
    • Stochastic Approximation EM (SAEM): Preferred for complex models (e.g., with ODEs) or highly sparse data, as it provides a more accurate stochastic assessment of the parameter integral [32].
  • Handling Censored Data (e.g., BLQ): For data below the limit of quantification, the Beal M3 method (likelihood-based) is precise but can be unstable. A pragmatic alternative is the M7+ method (impute zero, inflate additive error for BLQ points), which offers improved stability during model development with comparable bias and precision [63].

• Model Diagnostics & Refinement:

  • Evaluate goodness-of-fit plots: observations vs. population/individual predictions, conditional weighted residuals.
  • Perform a visual predictive check (VPC) to assess simulation properties.
  • Conduct stepwise covariate modeling (forward inclusion/backward elimination) using objective function value (OFV) changes.

• Model Qualification:

  • Finalize parameter estimates, compute confidence intervals via bootstrap or sampling importance resampling (SIR), and prepare model for simulation.

Protocol 2: AI/ML Model Development & Benchmarking Protocol

This protocol describes the process for developing and validating an AI/ML predictor, such as a neural network, for concentration or parameter prediction, tailored for comparison against a NONMEM MM model.

• Problem Framing & Data Preparation:

  • Define Task: Regression (predicting drug concentration) or classification (predicting dose group).
  • Curate Dataset: Use the same dataset as the NONMEM analysis. Features may include time, dose, demographic covariates, genetic markers, and lab values [84].
  • Preprocess: Handle missing values, scale/normalize features, and split data into training, validation, and test sets (e.g., 70/15/15). Ensure the test set is completely held out from training.

• Model Selection & Training:

  • Algorithm Choice: Based on [83] [84], select from:
    • Gradient Boosting (XGBoost, LightGBM): Often high-performing with structured data.
    • Neural Networks (Multilayer Perceptron): For capturing complex interactions.
    • Neural ODE: To embed a mechanistic PK structure within a neural network framework [83].
  • Training: Use the training set to fit the model. Employ K-fold cross-validation on the training set to tune hyperparameters (e.g., learning rate, network depth) and prevent overfitting [85].

• Benchmarking vs. NONMEM:

  • Prediction: Generate predictions on the identical, unseen test set using the final trained AI/ML model and the final estimated NONMEM model.
  • Performance Calculation: Compute and compare key metrics for both models:
    • Root Mean Squared Error (RMSE)
    • Mean Absolute Error (MAE)
    • Coefficient of Determination (R²)

• Explainability & Integration:

  • Perform feature importance analysis (e.g., SHAP values for tree-based models) to interpret predictions.
  • For hybrid approaches, consider using the AI model to inform covariate relationships or initial parameter estimates for a subsequent NONMEM run.

Visualizing the Hybrid AI-NONMEM Workflow

The integration of AI and traditional modeling is a powerful emerging paradigm. The following diagram illustrates a synergistic workflow where AI augments and informs the classic NONMEM modeling process.

Diagram 1: Integrated AI-NONMEM Workflow for Enhanced Model Development (Max Width: 760px)

The Scientist's Toolkit: Essential Research Reagent Solutions

Table 2: Key Software and Tools for Performance Benchmarking

Tool Category	Specific Tool/Name	Primary Function in Research	Application Context
Traditional NLMEM Engine	NONMEM (ICON plc)	Gold-standard software for population PK/PD parameter estimation via NLMEM.	Core engine for developing traditional MM and other PK models [83] [32].
AI/ML Modeling Frameworks	Python (Scikit-learn, PyTorch, TensorFlow)	Provides libraries for building, training, and validating a wide array of ML and DL models.	Implementing XGBoost, Neural Networks, Neural ODEs for predictive modeling [83] [84].
Automated PopPK Search	pyDarwin	Implements global optimization algorithms (e.g., Bayesian Optimization) to automate popPK model structure search.	Rapid, reproducible identification of optimal model structures from a pre-defined space [69].
LLM for Code Assistance	OpenAI o1 / GPT-4.1	Generates accurate foundational NONMEM code for standard tasks, accelerating model coding.	Assisting in writing basic NONMEM control streams; requires expert review for complex models [86].
Data Handling & Censoring	M7+ Method (Impute Zero, Inflate Error)	A pragmatic method for handling BLQ data, offering stability during model development.	Alternative to the more precise but less stable Beal M3 method in NONMEM [63].

The pursuit of precise Michaelis-Menten parameter estimation using NONMEM represents a cornerstone of modern pharmacometrics, providing a robust framework for understanding enzyme-mediated nonlinear pharmacokinetics. Within this established paradigm, a significant methodological evolution is underway with the emergence of Neural Ordinary Differential Equations (Neural ODEs). This hybrid approach synthesizes the principled, interpretable structure of differential equations with the adaptive, data-driven learning capacity of neural networks [87]. Traditional Nonlinear Mixed Effects (NLME) modeling, while powerful, operates under predefined structural assumptions and can be challenged by high-dimensional covariate relationships [88]. Neural ODEs offer a compelling alternative by learning the underlying system dynamics directly from observed data, using a neural network to parameterize the right-hand side of an ODE system [89] [90]. This fusion creates a tool that is not intended to replace mechanistic modeling but to augment it—particularly in scenarios where system dynamics are complex, partially unknown, or involve intricate covariate interactions that are difficult to specify a priori [91]. The integration of low-dimensional Neural ODE structures into pharmacometric software like Monolix and NONMEM marks a pivotal step toward practical application, enabling these models to account for inter-individual variability and serve as powerful support models within the traditional NLME workflow [92]. This document details the application notes and protocols for leveraging Neural ODEs within the context of advanced pharmacokinetic research.

Performance Benchmarking: Neural ODEs vs. Traditional PK Models

Empirical studies demonstrate the potential advantages of Neural ODEs, particularly in generalization and covariate integration. The following tables summarize key quantitative findings from recent applications.

Table 1: Cross-Regimen Generalization Performance with T-DM1 Data [93]

Model	Training Regimen	Test Regimen	Key Performance Metric	Result
Neural ODE	Q3W (3-weekly)	Q1W (weekly)	Prediction Accuracy	Substantially better than ML/DL comparators
LSTM Network	Q3W (3-weekly)	Q1W (weekly)	Prediction Accuracy	Poor generalization to unseen regimen
LightGBM	Q3W (3-weekly)	Q1W (weekly)	Prediction Accuracy	Poor generalization to unseen regimen
Neural ODE	Q1W (weekly)	Q3W (3-weekly)	Prediction Accuracy	Substantially better than ML/DL comparators
Traditional PopPK	Q3W (3-weekly)	Q1W (weekly)	Extrapolation Capability	Reasonable, but model-specific

Table 2: Predictive Accuracy on Sparse Dalbavancin PK Data (6-fold CV) [88] [94]

Model Type	Covariate Handling	Mean Prediction Error	Relative Performance
Two-Compartment Model	Without Covariates	Baseline	Reference
NLME Model	With Covariate Search	Comparable to Baseline	Similar to compartment model
Neural ODE	Without Covariates	Comparable to Baseline	Matches state-of-the-art NLME
Neural ODE	With Integrated Covariates	Superior Accuracy	Best performance, leveraging complex covariate structures

Table 3: NONMEM Estimation Methods for Complex Models [32]

Estimation Method	Principle	Best For	Computational Cost
First Order (FO)	Linearizes inter & intra-subject variability	Simple PK models, initial estimates	Low
FOCE w/ Interaction	More accurate approximation of random effects	Standard for most PopPK/PD models	Moderate
Monte Carlo SAEM	Stochastic approximation of exact integral	Complex models (e.g., ODEs, >6 params)	High, but efficient for complex problems
Importance Sampling (IMP)	Monte Carlo integration around mode	Final evaluation, standard error calculation	High

Core Experimental Protocol: Developing a Neural ODE PK Model

This protocol outlines the key steps for constructing and validating a Neural ODE model for pharmacokinetic data, integrating lessons from recent case studies [93] [92] [88].

3.1 Data Preparation and Preprocessing

• Data Structure: Organize data in a subject-centric format. Essential columns include: subject ID (ID), time (TIME), drug concentration (DV), dosing amount (AMT), dosing interval/regimen indicator, and cycle number (CYCLE) [93]. For covariate modeling, append columns like age, weight, and biomarkers.
• Feature Engineering for Time Series: For multi-cycle data, incorporate the first cycle's concentration profile (PK_cycle1) as a predictive feature for subsequent cycles [93]. Handle values below the limit of quantification (BLQ) as per standard PK practices (e.g., omission or M3 method) [32].
• Data Augmentation for Sparse Data: To counteract overfitting with small datasets (N~200), employ data augmentation in pre-training. This can involve adding Gaussian noise to observed concentrations or simulating virtual subjects by perturbing covariates within plausible ranges [88].

3.2 Neural ODE Architecture Specification

• Low-Dimensional Network Design: Use a shallow network (e.g., one hidden layer with 5-20 neurons) to ensure identifiability and reduce overfitting, aligning with pharmacometric principles [87] [91]. A sample formulation for a one-dimensional state (concentration) is: dh(t)/dt = f_NN(h(t), t, covariates; θ) where f_NN is a neural network with ReLU activation and θ are its weights [92] [91].
• Covariate Integration: Directly feed static covariates into the neural network alongside the state h(t) and time t, allowing the model to learn complex, non-linear covariate-effect relationships directly from data [88].
• Mechanistic Hybridization: For partially known systems, combine a mechanistic ODE with a neural network component. For example, a known PK model structure can be used while a neural network approximates an unknown PD relationship or a complex absorption process [92] [87].

3.3 Model Training and Estimation

• Loss Function: Minimize the mean squared error (MSE) between observed and predicted concentrations [88] [90].
• Optimization in NONMEM/Monolix: When implemented as an NLME model, use the SAEM estimation algorithm for stability with complex ODEs [32] [92]. Increase the maximum number of iterations (e.g., to 1000). For parameters without inter-individual variability (IIV), test both the "no variability" and "variability at the first stage" estimation methods [92].
• Parameter Initialization: Crucial for convergence. Initialize neural network weights (e.g., W, b) such that neurons are not dead (e.g., W*state + b > 0 initially). Use software auto-initialization features followed by manual adjustment [92]. Initial estimates for traditional PK parameters (e.g., CL, V) should follow standard practices.

3.4 Model Diagnostics and Validation

• Diagnostics: Evaluate standard goodness-of-fit plots: observed vs. population/individual predictions, conditional weighted residuals vs. time/predictions. Simulate from the fitted model to create Visual Predictive Checks (VPCs) [92].
• Interpretability Analysis: Employ SHapley Additive exPlanations (SHAP) to interpret how the Neural ODE uses input covariates for predictions, providing insight into learned covariate relationships [88] [94].
• Validation: Perform cross-validation (e.g., 6-fold) to assess robustness, especially with sparse data [88]. The ultimate test is external validation on a truly unseen dosing regimen to confirm superior generalizability [93].

Implementation Workflow: From NONMEM to a Hybrid Framework

Table 4: Software and Computational Toolkit

Tool	Primary Use	Key Feature for Neural ODEs	Reference
NONMEM (v7.5+)	Industry-standard NLME modeling.	Supports ODEs; SAEM algorithm suitable for complex NODE estimation.	[32] [92]
Monolix Suite (2023R1+)	User-friendly NLME modeling.	Explicit tutorial for implementing low-dimensional Neural ODEs.	[92]
PyTorch / torchdiffeq	Flexible DL research in Python.	Provides differentiable ODE solvers for custom NODE development and prototyping.	[88] [90]
R (rxode2, torch)	Pharmacometrics & statistics.	Enables NODE prototyping and integration with statistical analysis pipelines.

Table 5: Data and Modeling Components

Component	Description	Protocol Consideration
Rich Time-Series PK Data	Multi-cycle, multi-regimen data (e.g., T-DM1 dataset).	Essential for testing model generalization across regimens [93].
Patient Covariates	Demographics, lab values, biomarkers.	Feed directly into NODE to learn complex effect relationships [88].
Low-Dim NN Architecture	Shallow network (1-2 hidden layers, <20 neurons).	Prevents overfitting on sparse PK data; aligns with PK principles [87] [91].
SAEM Estimation Algorithm	Stochastic Approximation EM.	Preferred method in NONMEM/Monolix for stable NODE parameter estimation [32] [92].
SHAP Analysis Library	SHapley Additive exPlanations.	Critical for interpreting the "black box" and understanding covariate influence [88].

This analysis evaluates key quantitative modeling paradigms—Nonlinear Mixed-Effects (NLME) modeling, Machine Learning (ML), and emerging hybrid and fractional approaches—within the specific context of Michaelis-Menten (M-M) enzyme kinetics and pharmacokinetic (PK) research. The central thesis frames NLME software like NONMEM as the historical and contemporary standard for reliable parameter estimation (e.g., Vmax, Km) in M-M systems [24]. However, the field is rapidly evolving with the introduction of data-hungry ML methods promising predictive power [95], mechanistic fractional models offering flexible dynamics [17], and Large Language Models (LLMs) entering as potential assistive tools [96]. The critical appraisal of these paradigms hinges on three pillars: interpretability (the mechanistic transparency of the model), extrapolation (performance beyond the conditions of the training data), and data requirements (the volume and quality of data needed for development and reliable application). Understanding these trade-offs is essential for selecting a fit-for-purpose model in drug development [43].

Table: Comparative Analysis of Modeling Paradigms in Pharmacometrics

Paradigm	Core Strength	Key Limitation	Interpretability	Extrapolation Capability	Typical Data Requirements
NLME (NONMEM)	Robust, gold-standard for parameter estimation; quantifies population & individual variability [32].	Can be computationally intensive; model building can be iterative and time-consuming.	High (Mechanistic parameters like CL, Vd, Vmax, Km).	Strong within the mechanistic domain of the model [43].	Sparse to rich longitudinal data; handles unbalanced designs well.
Machine Learning (ML)	High predictive accuracy from complex, high-dimensional data; automates pattern discovery [95].	"Black-box" nature; risk of false correlations; poor out-of-domain extrapolation.	Low (Correlative features, not causal mechanisms).	Generally poor (Data-driven, interpolative).	Very large datasets required for training and validation.
Hybrid (PPK-ML)	Augments PPK predictability with ML; can improve precision when data are limited [95].	Complexity in integration; interpretability can be intermediate.	Medium to High (Depends on PPK core).	Improved over pure ML, guided by PPK structure.	Moderate to large; leverages PPK model to reduce pure ML data needs.
Fractional PK (FDEs)	Describes "anomalous" kinetics (e.g., power-law) with fewer parameters; memory effects [17].	Novel mathematical framework; less familiar to researchers; specialized software needed.	Medium (Parameters lack classic physiological analogs).	Potentially strong within its mathematical domain.	Similar to classic NLME.
Large Language Models (LLMs)	Assistive tool for code generation, literature synthesis, and workflow automation [96].	Hallucinations; lack of pharmacometrics-specific training data; not a standalone modeling tool.	Low for modeling, High for text tasks.	Not applicable for direct PK/PD prediction.	Not applicable (Used as tool, not a data-fitting model).

NONMEM Estimation Methods for Michaelis-Menten Kinetics

Parameter estimation for the M-M equation (V = (Vmax * [S]) / (Km + [S])) is foundational. A simulation study comparing linearization methods (e.g., Lineweaver-Burk) to nonlinear estimation within NONMEM demonstrated the clear superiority of the nonlinear approach. When estimating Vmax and Km from in vitro elimination kinetic data, nonlinear methods provided the most accurate and precise results, particularly when data incorporated a realistic combined (additive + proportional) error model [24]. NONMEM offers a suite of estimation algorithms, each with specific utility for problems of varying complexity.

Table: Key NONMEM Estimation Methods for PK/PD Modeling

Method (Guide)	Key Principle	Best Use Case	Relative Speed	Note on M-M Kinetics
First Order (FO) [32]	Linearizes inter-individual variability.	Initial screening, simple models.	Fast	May be inaccurate for highly nonlinear M-M.
FOCE [32]	Conditional estimation; more accurate approximation than FO.	Standard workhorse for most PK/PD models.	Moderate	Preferred over FO for M-M parameter estimation.
FOCE with INTERACTION [32]	Accounts for interaction between inter & intra-individual error.	Models with proportional or combined error structures.	Moderate	Crucial for M-M with combined error models [24].
Laplace [32]	Second-order conditional estimation.	Non-normal data, highly nonlinear models.	Slower	Useful for complex PD or categorical data linked to PK.
IMP [32]	Monte Carlo Expectation Maximization (exact method).	Complex models (e.g., ODEs, >6 params), sparse data.	Slow (Stochastic)	Excellent for precise M-M estimation if computational cost is acceptable.
SAEM [32]	Stochastic Approximation EM (exact method).	Very complex models, population models with mixtures.	Slow (Stochastic)	Efficient for large problems; often used with IMP for final estimates.

Detailed Experimental and Simulation Protocols

Protocol 1: Simulation Study for Comparing M-M Estimation Methods [24]

• Objective: To evaluate the accuracy and precision of Vmax and Km estimates from traditional linearization vs. nonlinear mixed-effects methods.
• Step 1 – Data Simulation:
  • Use a pharmacokinetic simulation tool (e.g., R) to generate 1000 replicate datasets.
  • Simulate substrate concentration ([S]) over time based on a known M-M model with defined true Vmax and Km.
  • Incorporate realistic residual error: 1) Additive error model, and 2) Combined (additive + proportional) error model.
• Step 2 – Parameter Estimation:
  • Apply multiple estimation methods to each replicate dataset.
  • Linearization Methods: Include Lineweaver-Burk, Eadie-Hofstee, etc.
  • Nonlinear Method: Implement using NONMEM (FOCE with INTERACTION recommended).
• Step 3 – Performance Evaluation:
  • For each method and replicate, calculate the estimated Vmax and Km.
  • Compute Relative Bias: (Median of Estimates - True Value) / True Value.
  • Compute Precision: Use the 90% confidence interval of the estimates.
  • Compare methods: The one with bias closest to zero and the narrowest confidence intervals is superior.
• Key Finding: Nonlinear estimation via NONMEM provided the most accurate and precise parameter recovery, especially under the combined error model [24].

Protocol 2: Developing a Hybrid PPK-ML Model for Vancomycin Dosing [95]

• Objective: To develop and compare a hybrid model against pure PPK and ML models for predicting vancomycin exposure (AUC24) in sepsis patients.
• Step 1 – Data Curation:
  • Source electronic health record data (e.g., from MIMIC-IV).
  • Include patient covariates (age, weight, serum creatinine), dosing records, and concentration measurements.
  • Split data into a training set (for model development) and a test set (for validation).
• Step 2 – Base PPK Model Development:
  • Use NONMEM to develop a population PK model (e.g., 1- or 2-compartment).
  • Estimate typical population parameters (CL, V), inter-individual variability (IIV), and residual error.
  • Perform covariate analysis (e.g., weight on CL, creatinine clearance on CL).
• Step 3 – Hybrid/ML Model Development:
  • Extract empirical Bayes estimates (EBEs) of individual PK parameters (CLi, Vi) from the final NONMEM model.
  • Use these EBEs as additional input features alongside original covariates in an ML algorithm (e.g., Random Forest, XGBoost).
  • Train the ML model to predict drug concentration or directly AUC24.
• Step 4 – Validation & Comparison:
  • Apply the standalone PPK model, the standalone ML model (trained without EBEs), and the hybrid model to the test set.
  • Compare predictive performance using metrics: Mean Absolute Prediction Error (MAPE), Root Mean Squared Error (RMSE).
  • Key Finding: The hybrid model often outperforms the pure PPK model when concentration data are unavailable, while Bayesian estimation (using the PPK model with concentration data) is best when concentrations are available [95].

Workflow for Model Evaluation and Stability

A critical challenge in pharmacometrics is ensuring model stability—where performance is reliable and not overly sensitive to small changes in data or settings. Instability manifests as convergence failures, unreasonable parameter estimates, or lack of standard errors [43]. The following diagnostic workflow, centered on NONMEM but applicable broadly, helps isolate the root cause, which typically lies in the balance between model complexity and data information content.

Workflow for Diagnosing Model Instability [43] A heuristic guide for diagnosing and resolving common model stability issues in pharmacometric analyses.

Workflow Narrative: The process begins by characterizing the nature of instability. If problems are systematic (e.g., consistently failing across runs), the issue likely relates to the fundamental mismatch between the chosen model's complexity and the information content provided by the experimental study design. For example, attempting to estimate a full target-mediated drug disposition (TMDD) model from data that only exhibits linear pharmacokinetics. The solution pathway involves model simplification, parameter fixing, or employing more robust estimation methods like IMP [43] [32].

Conversely, if instability is random or noisy (e.g., convergence depends on initial estimates), the root cause is more likely data quality or a model specification error. This pathway requires auditing data for outliers, verifying the residual error model, and meticulously checking the model code for non-syntactical errors (e.g., incorrect mapping of parameters) [43]. A stable model requires both a design that informs the parameters and high-quality data that aligns with the model's assumptions.

The Scientist's Toolkit: Essential Research Reagents and Software

Table: Key Research Reagent Solutions for PK/PD Modeling

Item	Category	Function in Research	Example/Note
NONMEM	Primary Modeling Software	The industry standard for NLME model development, estimation, and simulation.	Used for M-M parameter estimation [24], PPK model development [95].
R or Python	Statistical Computing & Scripting	Data preprocessing, visualization (ggplot2), post-processing of NONMEM outputs, running simulation studies.	Essential for implementing the simulation protocol in [24].
Monolix	Alternative Modeling Software	NLME modeling software with a different estimation engine (SAEM) and user interface.	Used as an alternative to NONMEM in some research and industry settings.
Xpose / Pirana	Diagnostics Toolkit	R-based (Xpose) or standalone (Pirana) tool for diagnostic model evaluation and run management.	Facilitates goodness-of-fit plots and covariate model diagnostics.
PDx-Pop	Commercial Interface	A commercial interface for NONMEM, providing a workflow management and graphical environment.	Common in industry to streamline modeling workflows.
Simulation Dataset	Virtual Research Reagent	A rigorously constructed simulated dataset with known "true" parameters.	Critical for method comparison (as in [24]) and assessing model performance.
Benchmark PK Dataset	Empirical Research Reagent	A well-curated, public real-world dataset (e.g., from critical care databases).	Used for developing and testing models like the vancomycin hybrid model [95].
Fractional Differential Equation Solver	Specialized Computational Tool	A numerical solver for implementing fractional PK models within an estimation framework.	Required for implementing the FDE approach described in [17].

The estimation of Michaelis-Menten parameters (V~max~ and K~m~) is a cornerstone of pharmacokinetics, critical for characterizing saturable metabolic and transport processes. While the underlying equation is well-established, the accuracy and precision of parameter estimation depend heavily on the chosen methodology and the software ecosystem that supports it [24]. Historically, researchers relied on linear transformation methods (e.g., Lineweaver-Burk, Eadie-Hofstee) which, while simple, can introduce significant bias and error propagation [24].

The advent of nonlinear mixed-effects modeling (NONMEM) software provided a paradigm shift, enabling direct fitting of the nonlinear Michaelis-Menten model to data. This approach, particularly within a population framework, allows for more robust estimation by accounting for inter-individual variability and complex residual error structures [24] [26]. The true power of NONMEM, however, is unlocked through its integration with a suite of auxiliary tools. This ecosystem, featuring PsN (Perl-speaks-NONMEM) for automation and advanced statistics, Pirana as a graphical workflow manager, and resources like NONMEMory for model libraries, has evolved into an indispensable platform for pharmacometric research [97] [98].

This integration directly addresses the findings of simulation studies which demonstrate that nonlinear estimation methods via NONMEM yield more reliable parameter estimates compared to traditional linearization techniques, especially with complex error models [24]. The evolution of this ecosystem—from standalone NONMEM execution to a connected, efficient workflow—forms the operational backbone of modern, model-informed drug development for Michaelis-Menten and other complex analyses.

Integrated Toolbox: Core Components and Their Synergistic Functions

The modern NONMEM-centric workflow is supported by specialized tools that manage, execute, and diagnose complex modeling tasks. Their roles are distinct but highly interconnected.

Pirana serves as the central graphical workbench and project manager. It provides a unified interface to organize model files, datasets, and output results. Its primary function is to streamline the execution of NONMEM runs through other tools in the ecosystem. For instance, it can launch PsN commands directly from its interface, manage remote computation hosts, and automatically refresh results upon job completion [99]. Recent versions have expanded its scope beyond NONMEM to integrate additional modeling engines like the NLME engine via R, and machine learning packages such as pyDarwin for automated model building [97].

PsN (Perl-speaks-NONMEM) is the computational engine for automation and advanced diagnostics. It is a command-line toolkit built on Perl modules that wraps around NONMEM to perform tasks impractical to code manually [98]. Its functions are critical for rigorous model evaluation and development:

• Automated Workflows: Tools like the stepwise covariate model (scm) automate the tedious process of testing covariate relationships.
• Model Diagnostics: Tools such as vpc (Visual Predictive Check) and simeval (simulation-based evaluation) are essential for assessing model predictive performance.
• Robustness Assessment: Routines like bootstrap (for confidence intervals) and cdd (case deletion diagnostics) evaluate the stability and reliability of parameter estimates [98].

NONMEM remains the core estimation engine. The latest version, NONMEM 7.6, includes advanced algorithms like Stochastic Approximation Expectation-Maximization (SAEM) and Markov-Chain Monte Carlo Bayesian Analysis (BAYES), which are particularly suited for complex nonlinear models [20]. Its NM-TRAN preprocessor allows models to be specified in a user-friendly control stream format.

The synergy is clear: A modeler uses Pirana to organize the project and then, with a click, launches a PsN vpc command. PsN automatically handles the simulation, NONMEM re-execution, and result compilation, with outputs neatly organized back into the Pirana interface for review [99] [97]. This seamless integration drastically reduces manual effort and potential for error.

Table 1: Core Software Components in the NONMEM Ecosystem for Michaelis-Menten Analysis

Software	Primary Role	Key Function in Michaelis-Menten Context	Interface
NONMEM 7.6	Gold-standard estimation engine [20]	Fits nonlinear Michaelis-Menten model using FOCE, SAEM, or other algorithms; estimates population V~max~ and K~m~ with variability.	Command-line, controlled via text files.
PsN (v5.6.0)	Automation & advanced statistics toolkit [98]	Automates VPC, bootstrap, covariate search, and model diagnostics to validate saturable PK model performance.	Command-line (executed directly or via Pirana).
Pirana	Modeling workbench & project manager [97]	Provides GUI to manage control streams, data, outputs; integrates and launches NONMEM/PsN; visualizes diagnostic plots.	Graphical User Interface (GUI).

Application Notes & Protocols: Michaelis-Menten Parameter Estimation

Protocol: Simulation-Based Assessment of Estimation Methods

Objective: To compare the accuracy and precision of traditional linearization methods versus nonlinear mixed-effects estimation (using NONMEM) for determining V~max~ and K~m~ from in vitro drug elimination kinetic data [24].

Background: This protocol is based on a published simulation study by Cho et al. (2018), which demonstrated the superiority of nonlinear methods [24] [100]. The following is a detailed methodology for replicating and extending such an analysis using the integrated PsN/Pirana environment.

Materials & Software Requirements:

• Software: NONMEM (v7.4 or higher), PsN (v4.8 or higher), Pirana, R statistical software.
• Hardware: Computer with multi-core processor and ≥ 2 GB RAM dedicated to NONMEM [20].

Experimental/Simulation Procedure:

• Data Simulation in R:

  • Generate 1000 replicate datasets mimicking a typical in vitro incubation study.
  • Use a prior V~max~ and K~m~ as population truths (e.g., from literature).
  • Simulate substrate concentration ([S]) over time via numerical integration of the Michaelis-Menten ODE: -d[S]/dt = (V~max~ * [S]) / (K~m~ + [S]).
  • Incorporate realistic residual error: either an additive error model (e.g., constant standard deviation) or a combined error model (constant + proportional), adding random noise via Monte Carlo simulation [24].

• Model Development in Pirana/NONMEM:

  • Control Stream Creation: Write a NONMEM control stream (*.mod) defining the structural model.
    • Use $PRED to code the integrated form of the Michaelis-Menten equation or use $DES with ADVAN13 for differential equation solution.
    • Define parameters VMAX and KM with typical population values (THETA) and inter-individual variability (ETA) via an exponential model.
    • Define residual error (EPSILON) according to the simulation model (additive or combined).
  • Dataset Formatting: Prepare the data file (*.csv) with columns for ID, TIME, DV (measured [S]), EVID, and potentially AMT if simulating dosing.

• Automated Execution with Pirana & PsN:

  • Load the control stream and data file into a Pirana project.
  • Use Pirana's "Execute" dialog (Ctrl-E) to run the base model. In the advanced view, select the PsN configuration and number of CPU nodes for parallel processing [99].
  • The typical PsN command for a basic NONMEM run initiated from Pirana would be: execute <model_name>.mod -dir=<run_directory>.
  • For the simulation study, this base estimation (using FOCE or SAEM) would be performed on each of the 1000 replicate datasets. This can be automated using a PsN script or a custom R loop that modifies the data file path for each run.

Statistical Analysis Plan:

• Parameter Estimation: For each replicate dataset, estimate parameters using:
  • Traditional Methods: Linear transformations (Lineweaver-Burk, Eadie-Hofstee).
  • NONMEM: Nonlinear mixed-effects estimation (FOCE method).
• Performance Metrics: For each method and each parameter (V~max~, K~m~), calculate:
  • Relative Bias: (Median Estimate - True Value) / True Value * 100%
  • Precision: Width of the 90% confidence interval (CI) for the estimates across replicates.
• Comparison & Visualization: Use R (potentially via PsN's rplots option [98]) to generate comparative boxplots of bias and tables of CI widths for all methods.

Expected Outcome: As demonstrated by Cho et al., the nonlinear estimation via NONMEM is expected to show significantly lower median bias and tighter confidence intervals, particularly for data generated with a combined error model, confirming its superior reliability [24].

Table 2: Performance Comparison of Estimation Methods for Michaelis-Menten Parameters (Simulated Data)

Estimation Method	V~max~ Relative Bias (%)	K~m~ Relative Bias (%)	Remarks / Key Advantage
Lineweaver-Burk (Linear)	High Positive Bias [24]	High Negative Bias [24]	Simple but statistically flawed; distorts error structure.
Eadie-Hofstee (Linear)	Moderate Bias [24]	Moderate Bias [24]	Better than Lineweaver-Burk but still suboptimal.
NONMEM (FOCE)	Lowest Bias [24]	Lowest Bias [24]	Directly models nonlinearity and correct error structure; handles population data.
NONMEM (SAEM)	Theoretically Lower Bias	Theoretically Lower Bias	More robust for complex models or sparse data; available in NONMEM 7.6 [20].

The Scientist's Toolkit: Essential Research Reagent Solutions

Table 3: Essential Software Tools & Resources for Michaelis-Menten PK/PD Research

Tool/Resource Name	Category	Primary Function	Application in Michaelis-Menten Context
NONMEM 7.6 [20]	Estimation Engine	Nonlinear mixed-effects modeling and simulation.	Gold-standard for population estimation of V~max~ and K~m~ with inter-individual variability.
PsN Toolkit [98]	Automation & Diagnostics	Perl-based modules for automating NONMEM runs and advanced statistics.	Automates VPC, bootstrap, and covariate search for saturable PK models.
Pirana [97]	Workbench / GUI	Integrated modeling environment for managing runs, outputs, and diagnostics.	Central hub for project management, visual diagnostics, and executing NONMEM/PsN workflows.
R / nlmixr2 Ecosystem [101]	Complementary Framework	Open-source platform for pharmacometrics; includes nlmixr2 for NLME modeling.	Alternative estimation environment; packages like ggPMX and vpc provide diagnostic plots compatible with NONMEM outputs.
Xpose / ggPMX	Diagnostic Visualization	R packages for standardized goodness-of-fit and diagnostic plotting.	Generates publication-quality plots (e.g., predictions vs. observations, residual diagnostics) for model evaluation [101].
Model Libraries (NONMEMory / nlmixr2lib)	Knowledge Repository	Community-shared collections of canonical models.	Provides templates and starting points for coding Michaelis-Menten elimination or absorption models [101].
Pharmpy	Model Conversion & Toolbox	Python toolkit for pharmacometric analysis.	Can assist in converting models between formats (e.g., NONMEM to nlmixr2) and in automated model building [101].

Advanced Applications and Future Directions

The integrated ecosystem is expanding beyond traditional pharmacokinetic modeling. Pirana now integrates machine learning packages like pyDarwin, which can automatically search vast spaces of model structures, random effects, and covariate relationships [97]. This is particularly valuable for complex saturable systems where the standard Michaelis-Menten model may need extension (e.g., incorporating auto-inhibition or time-dependent degradation).

Furthermore, the rise of the open-source nlmixr2 ecosystem in R represents a parallel and interoperable evolution. It includes tools for automatic model initialization (nlmixr2autoinit), simulation (Campsis), and optimal design (PopED) [101]. Crucially, conversion tools like babelmixr2 and pharmpy allow models to be translated between NONMEM and nlmixr2 formats, fostering collaboration and method comparison [101].

Future directions, as highlighted by surveys in quantitative systems pharmacology (QSP), point toward a need for even better scripting capabilities, high-performance computing integration, and enhanced visualization [102]. These needs are being met through improved parallel computing in NONMEM 7.6 [20], cloud-based execution options, and the continuous development of R and Python packages for advanced diagnostics and reporting. The enduring goal is a cohesive, efficient, and transparent software environment that accelerates the translation of complex kinetic models, like Michaelis-Menten systems, into actionable drug development decisions.

Conclusion

The reliable estimation of Michaelis-Menten parameters using NONMEM remains a cornerstone for characterizing nonlinear pharmacokinetics in drug development. This guide has synthesized the journey from foundational theory and practical implementation to resolving instability and validating outcomes. The future of this field lies in the strategic integration of traditional, robust NLME methods with emerging technologies. This includes adopting automated pipelines for generating initial estimates to improve efficiency and reproducibility [citation:3], leveraging AI/ML models for specific predictive tasks where they excel [citation:2], and utilizing advanced algorithms within NONMEM itself for complex optimal dosing challenges [citation:4]. As these tools converge, pharmacometricians will be empowered to build more stable, predictive models faster, ultimately accelerating the delivery of safe and effective therapies, especially for drugs exhibiting saturable, target-mediated disposition.

References

• 1. Michaelis–Menten kinetics [https://en.wikipedia.org/wiki/Michaelis%E2%80%93Menten_kinetics]
• 2. Michaelis Menten Kinetics - an overview [https://www.sciencedirect.com/topics/immunology-and-microbiology/michaelis-menten-kinetics]
• 3. Michaelis-Menten Kinetics [https://chem.libretexts.org/Bookshelves/Biological_Chemistry/Supplemental_Modules_(Biological_Chemistry)/Enzymes/Enzymatic_Kinetics/Michaelis-Menten_Kinetics]
• 4. Comparison of various estimation methods ... [https://synapse.koreamed.org/articles/1094566]
• 5. Application of modified Michaelis – Menten equations for ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8507113/]
• 6. Michaelis-Menten equation – Knowledge and References [https://taylorandfrancis.com/knowledge/Medicine_and_healthcare/Medical_genetics/Michaelis-Menten_equation/]
• 7. An automated pipeline to generate initial estimates for ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12592298/]
• 8. R-based reproduction of the estimation process hidden ... [https://www.semanticscholar.org/paper/R-based-reproduction-of-the-estimation-process-%C2%AE-2-Bae-Yim/c3f78d95d7c999f2ecc789992a68a57c096f3c2c]
• 9. Drug Elimination - an overview [https://www.sciencedirect.com/topics/biochemistry-genetics-and-molecular-biology/drug-elimination]
• 10. Comparison of various estimation methods for the ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6989224/]
• 11. Advancing drug development with “Fit-for-Purpose” modeling ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12436579/]
• 12. Pharmacokinetics - StatPearls - NCBI Bookshelf - NIH [https://www.ncbi.nlm.nih.gov/books/NBK557744/]
• 13. Comparison of various estimation [https://tcpharm.org/DOIx.php?id=10.12793/tcp.2018.26.1.39]
• 14. Machine Learning for PK/PD Modeling in Drug Development [https://www.certara.com/blog/machine-learning-for-pk-pd-modeling-in-drug-development/]
• 15. Saturable Drug Absorption [https://www.certara.com/knowledge-base/saturable-drug-absorption/]
• 16. Statistical identifiability and convergence evaluation for ... [https://www.sciencedirect.com/science/article/abs/pii/S0169260713003313]
• 17. Implementation of non-linear mixed effects models defined ... [https://link.springer.com/article/10.1007/s10928-023-09851-1]
• 18. Chapter 1 - Introduction to NONMEM, PREDPP, and NM-TRAN [https://nmhelp.tingjieguo.com/V/1]
• 19. NONMEM Tutorial Part I: Description of Commands and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6709426/]
• 20. NONMEM | Nonlinear Mixed Effects Modelling [https://www.iconplc.com/solutions/technologies/nonmem]
• 21. NONMEM [https://en.wikipedia.org/wiki/NONMEM]
• 22. NONMEM Code [https://www.pharmacy.umaryland.edu/centers/ctm/learning-resources/nonmem-code/]
• 23. Basic NONMEM Workshop Instructions [https://holford.fmhs.auckland.ac.nz/teaching/PAWS/workshops/basic/instructions]
• 24. Comparison of various estimation methods for the ... [https://pubmed.ncbi.nlm.nih.gov/32055546/]
• 25. Tutorial for Modeling Delays in Biological Systems in the ... [https://pubmed.ncbi.nlm.nih.gov/40524365/]
• 26. Evaluation of the nonparametric estimation method in ... [https://www.sciencedirect.com/science/article/abs/pii/S0928098708005125]
• 27. Introduction to Pharmacokinetic Modeling Methods - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC3636497/]
• 28. Basic Concepts in Population Modeling, Simulation, and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3606044/]
• 29. Two NONMEM Tutorials in PSP! [https://www.ascpt.org/Journals/PSP/PSPost/View/ArticleId/24063/Two-NONMEM-Tutorials-in-PSP]
• 30. Chapter 4 - Models for Population Data - NONMEM Help [https://nmhelp.tingjieguo.com/V/4]
• 31. A Bayesian Approach for Population Pharmacokinetic ... [https://www.sciencedirect.com/science/article/pii/S0011393X1630131X]
• 32. NONMEM Tutorial Part II: Estimation Methods and Advanced ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6709422/]
• 33. Beginners Tutorial [https://www.pharmacy.umaryland.edu/centers/ctm/learning-resources/beginners-tutorial/]
• 34. Support software and resources [https://www.page-meeting.org/about-us/support-software-and-resources/]
• 35. NONMEM and R code for PKPD [https://pkpd-info.com/NONMEM.php]
• 36. I. Overview of PREDPP - NONMEM Help [https://nmhelp.tingjieguo.com/VI/I]
• 37. advan.ppp [https://pkpd-info.com/NONMEM/NM_guides/advan.htm]
• 38. User-Written Models [https://basicmedicalkey.com/user-written-models/]
• 39. des.for [https://pkpd-info.com/NONMEM/NM_guides/des.htm]
• 40. Chapter 7 - $SUBROUTINE Record and $PK Record [https://nmhelp.tingjieguo.com/V/7]
• 41. NONMEM Users Guide Part VI - PREDPP - Chapter I [https://nonmem.iconplc.com/nonmem/Nonmem_7_Project/nmvi2.0beta/htmlplus/VI/I.html]
• 42. An automated pipeline to generate initial estimates for ... [https://pubmed.ncbi.nlm.nih.gov/41199105/]
• 43. A Pharmacometric Workflow for Resolving Model Instability in ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12521063/]
• 44. The impact of misspecified covariate models on inclusion ... [https://link.springer.com/article/10.1007/s10928-025-09964-9]
• 45. Chapter 6 - NONMEM Help [https://nmhelp.tingjieguo.com/V/6]
• 46. Interpreting the NONMEM Output [https://basicmedicalkey.com/interpreting-the-nonmem-output/]
• 47. A modeller's perspective on EM methods versus FOCE ... [https://www.page-meeting.org/default.asp?abstract=11725]
• 48. Comparing the performance of first-order conditional ... [https://pubmed.ncbi.nlm.nih.gov/33884580/]
• 49. Estimation and Solvers - NONMEM - Viktor Rognås [https://vrognas.com/docs/tools-of-the-trade/nonmem/nm-est/]
• 50. Performance comparison of first-order conditional estimation ... [https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/s12874-017-0427-0]
• 51. NONMEM PK Templates [https://pmxrepo.com/nmcode.html]
• 52. Bayesian estimation in NONMEM - PMC - PubMed Central [https://pmc.ncbi.nlm.nih.gov/articles/PMC10864934/]
• 53. Tutorial for Modeling Delays in Biological Systems in the ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12256671/]
• 54. Tutorial for $DESIGN in NONMEM: Clinical trial evaluation ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8674001/]
• 55. Leveraging large language models in pharmacometrics [https://pubmed.ncbi.nlm.nih.gov/40464844/]
• 56. NONMEM model templates and Codes [https://pkpd-info.com/NONMEM/Model_templates.php]
• 57. Modelling pulsatile profiles in NONMEM [https://www.pmxsolutions.com/2019/10/09/modelling-pulsatile-profiles-in-nonmem-2/]
• 58. OptiDose: Computing the Individualized Optimal Drug Dosing ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8550736/]
• 59. Strategies for Dose Selection in Oncology Drug Development [https://www.caidya.com/strategies-for-dose-selection/]
• 60. Project Optimus [https://www.fda.gov/about-fda/oncology-center-excellence/project-optimus]
• 61. Computing optimal drug dosing regarding efficacy and safety [https://link.springer.com/article/10.1007/s10928-024-09940-9]
• 62. NONMEM on Metworx [https://kb.metworx.com/Users/Tutorials/Nonmem/Nonmem-on-Metworx/]
• 63. A Pragmatic Approach to Handling Censored Data Below ... [https://pubmed.ncbi.nlm.nih.gov/40067154/]
• 64. An automated pipeline to generate initial estimates for ... [https://link.springer.com/article/10.1007/s10928-025-10000-z]
• 65. NONMEM Overview and Writing an NM-TRAN Control ... [https://basicmedicalkey.com/nonmem-overview-and-writing-an-nm-tran-control-stream/]
• 66. 1. What This Chapter is About [https://nonmem.iconplc.com/nonmem/Nonmem_7_Project/nmvi2.0beta/htmlplus/V/11.html]
• 67. Introduction to Version VI - NONMEM Help [https://nmhelp.tingjieguo.com/intro/I]
• 68. A genetic algorithm based global search strategy for ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4294074/]
• 69. A machine learning approach to population ... [https://www.nature.com/articles/s43856-025-01054-8]
• 70. An Evolutionary Search Algorithm for Covariate Models in ... [https://www.sciencedirect.com/science/article/abs/pii/S0022354917302642]
• 71. An automated pipeline to generate initial estimates for population ... [http://47.251.13.51:8081/41199105/]
• 72. Automated Covariate Model Building Within NONMEM [https://link.springer.com/article/10.1023/A:1011970125687]
• 73. Help for package nlmixr2autoinit [https://cran.r-project.org/web/packages/nlmixr2autoinit/refman/nlmixr2autoinit.html]
• 74. NONMEMory: A run management tool for NONMEM [https://www.sciencedirect.com/science/article/abs/pii/S0169260705000581]
• 75. Visual predictive check | Monolix - MonolixSuite Documentation [https://monolixsuite.slp-software.com/monolix/2024R1/visual-predictive-check]
• 76. A Tutorial on Visual Predictive Checks [https://www.page-meeting.org/Abstracts/a-tutorial-on-visual-predictive-checks/]
• 77. A step-by-step guide to prediction corrected visual ... [https://www.pmxsolutions.com/2018/09/21/a-step-by-step-guide-to-prediction-corrected-visual-predictive-checks-vpc-of-nonmem-models/]
• 78. Visual Predictive Checks (VPC) • xpose - GitHub Pages [https://uupharmacometrics.github.io/xpose/articles/vpc.html]
• 79. A Regression Approach to Visual Predictive Checks for ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6202468/]
• 80. The Reference-Corrected Visual Predictive Check: A More ... [https://pubmed.ncbi.nlm.nih.gov/40299161/]
• 81. NONMEM's SIGDIG Convergence Criterion [https://holford.fmhs.auckland.ac.nz/research/sigdig]
• 82. Visual Predictive Checks (VPC) [https://cran.r-project.org/web/packages/xpose/vignettes/vpc.html]
• 83. A Comparative Analysis of NONMEM and AI-based Models ... [https://pubmed.ncbi.nlm.nih.gov/41254220/]
• 84. Artificial Intelligence and Machine Learning Applications to ... [https://www.mdpi.com/2079-6382/13/12/1203]
• 85. AI‐NLME: A New Artificial Intelligence‐Driven Nonlinear ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12405737/]
• 86. AI for NONMEM Coding in Pharmacometrics Research and ... [https://pubmed.ncbi.nlm.nih.gov/41187068/]
• 87. Low-dimensional neural ODEs and their application in ... [https://link.springer.com/article/10.1007/s10928-023-09886-4]
• 88. Leveraging Neural ODEs for Population Pharmacokinetics of ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12192077/]
• 89. Understanding Neural ODE's - Jonty Sinai [https://jontysinai.github.io/jekyll/update/2019/01/18/understanding-neural-odes.html]
• 90. Chapter 3: Neural Ordinary Differential Equations [http://implicit-layers-tutorial.org/neural_odes/]
• 91. Low-dimensional neural ODEs and their application in ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10982100/]
• 92. Using neural ODEs in Monolix | Tutorials [https://monolixsuite.slp-software.com/tutorials/2024R1/case-study-neural-odes]
• 93. Neural-ODE for pharmacokinetics modeling and its advantage ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8283337/]
• 94. Leveraging Neural ODEs for Population Pharmacokinetics ... [https://www.mdpi.com/1099-4300/27/6/602]
• 95. Machine learning and population pharmacokinetics [https://pmc.ncbi.nlm.nih.gov/articles/PMC12054080/]
• 96. Pharmacometrics in the Age of Large Language Models [https://pmc.ncbi.nlm.nih.gov/articles/PMC12567310/]
• 97. Pirana and Integrated PMX Tools, a Workbench for ... [https://pubmed.ncbi.nlm.nih.gov/40613737/]
• 98. PsN - Perl-speaks-NONMEM [https://uupharmacometrics.github.io/PsN/]
• 99. Using_NONMEM_through_PsN [https://onlinehelp.certara.com/pirana/23.10.1/Pirana_User_Guide/Pirana_NONMEM/Using_NONMEM_through_PsN.htm]
• 100. [PDF] Comparison of various estimation methods for the ... [https://www.semanticscholar.org/paper/Comparison-of-various-estimation-methods-for-the-of-Cho-Lim/0c92de62e2a1376fdd2cb4a642cd1b126953f081]
• 101. nlmixr2 ecosystem [https://blog.nlmixr2.org/blog/2025-06-30-nlmixr2-ecosystem/]
• 102. A Survey of Software Tool Utilization and Capabilities for ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6389347/]