Mastering Vmax and Km: Advanced Estimation Techniques for Enzyme Kinetics in Biomedical Research

Abstract

This article provides a comprehensive guide to Vmax and Km estimation in enzyme kinetics, tailored for researchers, scientists, and drug development professionals. It covers foundational principles of Michaelis-Menten kinetics, practical experimental and computational methods for parameter determination, strategies for troubleshooting and optimizing assays, and advanced techniques for validation and comparative analysis. The content integrates recent advancements, including Bayesian estimation, optimized experimental designs, and applications in predicting drug clearance and bioavailability, to support accurate and efficient research in drug discovery and development.

The Fundamentals of Vmax and Km: Core Concepts in Enzyme Kinetics

Foundational Definitions and Core Biological Meanings

The parameters Vmax (maximum velocity) and Km (Michaelis constant) are the principal quantitative descriptors in enzyme kinetics, derived from the Michaelis-Menten model first proposed in 1913 [1]. They provide an essential framework for understanding how enzymes function as biological catalysts, which accelerate biochemical reactions by lowering the activation energy required [2] [3].

Vmax is defined as the maximum rate of reaction achievable when all available enzyme active sites are saturated with substrate [1] [2]. It represents a plateau in the reaction velocity, where further increases in substrate concentration yield no increase in rate. Vmax is directly proportional to the total enzyme concentration ([ET]) and fundamentally reflects the catalytic capacity of the enzyme when substrate binding is not rate-limiting. It is mathematically defined as *Vmax = k₂[ET], where *k₂ (often denoted k_cat) is the catalytic rate constant for the conversion of the enzyme-substrate complex to product [4] [5].

Km, the Michaelis constant, is defined as the substrate concentration at which the reaction velocity is half of Vmax [1] [6]. It is a composite constant expressed in terms of microscopic rate constants: Km = (k₋₁ + k₂)/k₁, where k₁ and k₋₁ are the forward and reverse rate constants for substrate binding, and k₂ is the catalytic rate constant [4] [3]. Biologically, Km provides an inverse measure of the enzyme's apparent affinity for its substrate: a low Km value indicates high affinity, meaning the enzyme achieves half-maximal efficiency at low substrate concentrations, while a high Km indicates low affinity [1] [2].

Table 1: Core Definitions and Biological Interpretations of Vmax and Km

Parameter	Mathematical Definition	Biological Meaning	Interpretation of Value
Vmax	Vmax = k_cat · [E_T]	Maximum catalytic capacity when enzyme is saturated.	High Vmax = High turnover capacity. Dependent on enzyme concentration.
Km	Km = (k_₋₁ + k_cat)/k_₁	Substrate concentration at half-maximal velocity (Vmax/2).	Low Km = High apparent substrate affinity. High Km = Low apparent affinity.

Kinetic Significance in Catalytic Efficiency

The individual parameters Vmax and Km are most informative when considered together. Their ratio, k_cat/Km, known as the specificity or catalytic efficiency constant, is a critical metric for evaluating an enzyme's performance under non-saturating, physiologically relevant substrate concentrations [3] [7]. This constant has units of M⁻¹s⁻¹ and represents the enzyme's effectiveness in converting substrate to product when substrate is limiting.

A high k_cat/Km indicates high efficiency, resulting from a combination of a fast turnover rate (high k_cat, reflected in Vmax) and tight substrate binding (low Km) [7]. For example, the enzyme carbonic anhydrase has a k_cat/Km approaching the diffusion-controlled limit (~10⁸ M⁻¹s⁻¹), denoting a near-perfect catalyst [6]. This efficiency has direct biological implications: enzymes with high catalytic efficiency for specific substrates can effectively outcompete other enzymes for a shared, limited substrate pool within a cell [8].

The relationship between velocity (v), substrate concentration ([S]), Vmax, and Km is described by the fundamental Michaelis-Menten equation:

v = (Vmax [S]) / (Km + [S]) [2] [3]

This equation generates a rectangular hyperbola when reaction velocity is plotted against substrate concentration. The plot reveals two key kinetic regimes: 1) First-order kinetics at low [S] (where [S] << Km), where velocity is approximately proportional to substrate concentration, and 2) Zero-order kinetics at high [S] (where [S] >> Km), where velocity is independent of [S] and approaches Vmax [2] [6].

Diagram 1: Michaelis-Menten Enzyme Kinetic Pathway. This diagram illustrates the fundamental steps of enzyme catalysis, highlighting the microscopic rate constants (k₁, k₋₁, k_cat) that underlie the macroscopic parameters Vmax and Km [4] [5] [3].

The Research Context: Reliability and Interpretation of Parameters

Within the broader thesis of Vmax and Km estimation research, a paramount challenge is ensuring the reliability, accuracy, and appropriate interpretation of these parameters [8]. They are not universal constants but are dependent on experimental conditions such as temperature, pH, ionic strength, and buffer composition [8]. Consequently, a value reported in the literature is only valid for the specific conditions under which it was measured.

Key issues in research include:

• Assay Conditions: Many historical studies use conditions optimized for assay convenience rather than physiological relevance, complicating the integration of data for systems biology modeling [8].
• Parameter Variability: Estimates of Vmax and Km can show higher variability than derived parameters like intrinsic clearance (CLint), particularly when substrate turnover is low [9].
• Data Sources and Quality: Researchers often source parameters from databases like BRENDA or SABIO-RK [8]. The emerging STRENDA (STandards for Reporting ENzymology DAta) guidelines aim to improve reporting standards, requiring detailed methodological metadata to facilitate data assessment and reuse [8].

Furthermore, the interpretation of Km as a simple measure of affinity is most straightforward for classical, single-substrate Michaelis-Menten kinetics. Mechanisms become more complex with multi-substrate reactions (e.g., ordered-sequential, ping-pong mechanisms), allosteric enzymes, and membrane transporters [4] [8]. For instance, in transporter kinetics (e.g., solute carriers like ASBT or PEPT1), a simple Michaelis-Menten model is often an oversimplification of a multi-state translocation cycle involving unidirectional steps [4]. In such systems, Km and Vmax are complex functions of multiple microscopic rate constants governing binding, translocation, and release [4].

Table 2: Impact of Key Experimental Variables on Km and Vmax Estimates

Experimental Variable	Typical Effect on Km	Typical Effect on Vmax	Notes for Researchers
Enzyme Concentration	None (Theoretically independent)	Linear increase	Vmax must be normalized (e.g., per mg protein) for comparison across studies [6].
Temperature	Can increase or decrease	Usually increases to an optimum	Changes reflect alterations in rate constants and enzyme stability [8].
pH	Can change significantly	Usually has a clear optimum	Alters ionization states of active site residues, affecting binding (Km) and catalysis (Vmax) [2] [8].
Competitive Inhibitor	Increases (apparent Km)	No change	Classic diagnostic pattern. Inhibitor competes with substrate for the active site [1] [2].
Non-competitive Inhibitor	No change	Decreases	Inhibitor binds at a site other than the active site, reducing catalytic rate [1] [2].

Experimental Methodologies for Parameter Estimation

Accurate determination of Vmax and Km requires measuring the initial reaction rates (v₀) at a series of substrate concentrations ([S]) while keeping enzyme concentration constant [6] [8]. The "initial rate" is critical to avoid complications from product inhibition, substrate depletion, or enzyme inactivation.

Classical Protocol (Substrate Saturation Curve):

• Prepare a set of reaction mixtures with a fixed, known concentration of enzyme.
• In each mixture, use a different concentration of substrate, typically spanning a range from well below to well above the expected Km (e.g., 0.2Km to 5Km).
• Initiate the reaction and measure the amount of product formed (or substrate consumed) over a short, early time period where the relationship is linear.
• Plot the initial velocity (v₀) against substrate concentration ([S]) to obtain the hyperbolic Michaelis-Menten curve.
• Use non-linear regression to fit the data directly to the Michaelis-Menten equation, which is the preferred modern method for extracting Vmax and Km [9].

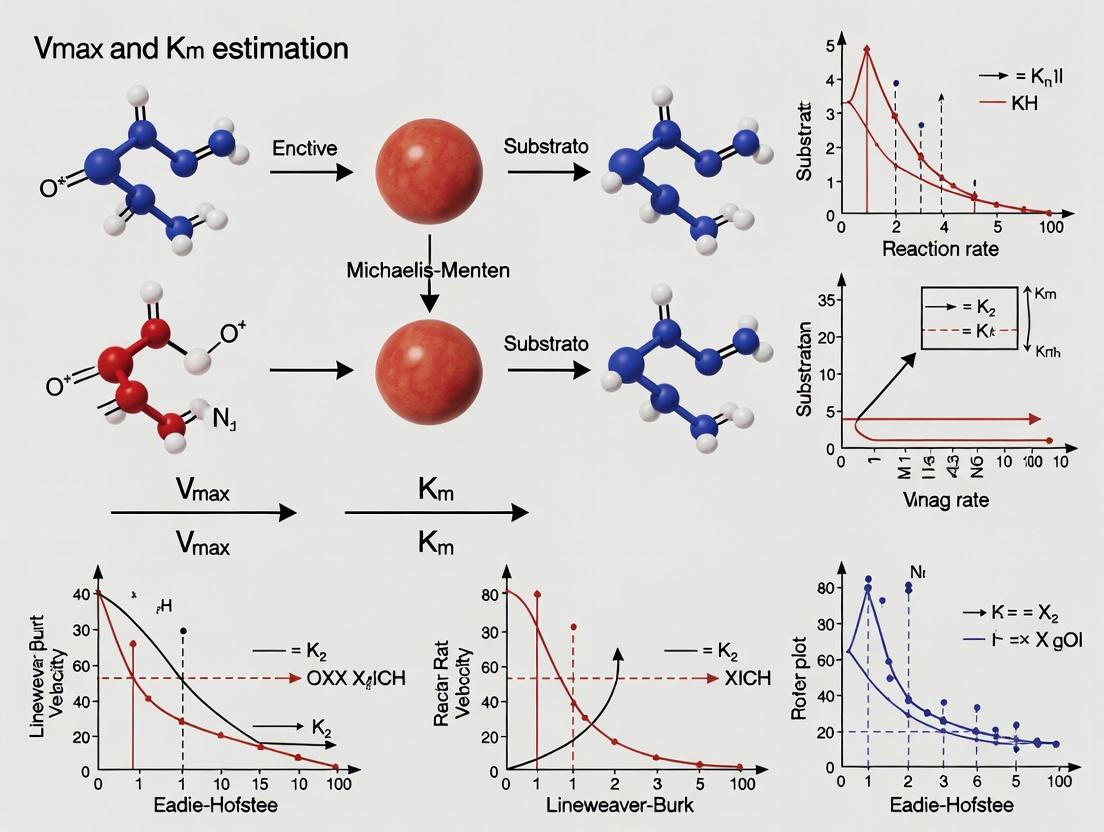
Linear Transformation (Lineweaver-Burk Plot): The hyperbolic relationship can be linearized by plotting 1/v₀ against 1/[S]. This Lineweaver-Burk plot yields a straight line where the y-intercept is 1/Vmax, the x-intercept is -1/Km, and the slope is Km/Vmax [2]. While historically important and useful for visualizing inhibition patterns (competitive, non-competitive), this method can distort experimental error and is less statistically reliable for parameter estimation than non-linear regression [2].

Advanced and Optimized Protocols: Recent research focuses on optimizing experimental design for efficiency and reliability, particularly in drug discovery. The Optimal Design Approach (ODA) uses multiple substrate starting concentrations with strategically chosen late sampling time points. This method, validated against richer "multiple depletion curves" methods, provides reliable estimates of Vmax, Km, and intrinsic clearance (CLint) even with a limited total number of samples [9].

Diagram 2: Experimental Workflow for Estimating Vmax and Km. This flowchart outlines the standard process from experiment initiation to parameter estimation, highlighting the two primary analysis pathways [6] [9].

Advanced Applications and Biological Scaling

The principles of Vmax and Km extend beyond soluble enzymes to critical applications in drug development and systems biology.

In pharmacology and toxicology, these parameters are used to characterize the metabolism of drugs by cytochrome P450 enzymes and their transport by membrane carriers [4] [9]. Determining the Km for a drug's metabolism is essential for assessing the risk of non-linear pharmacokinetics, where saturation of metabolic pathways at clinical doses leads to disproportionate increases in drug exposure [9].

From an evolutionary and ecological perspective, fundamental scaling relationships exist between kinetic parameters and cellular physiology. Research on phototrophic and chemotrophic microorganisms reveals a trade-off between Vmax and Km, often following power-law relationships with cell size [10]. Generally, larger cells have a higher maximum uptake capacity (Vmax), but this is associated with a higher Km (lower affinity). This Vmax-Km trade-off is a key constraint in microbial ecology and modeling, influencing competition for nutrients in environmental systems [10].

Table 3: The Scientist's Toolkit: Essential Reagents and Materials for Enzyme Kinetic Studies

Reagent/Material	Function in Experiment	Key Considerations
Purified Enzyme	The catalyst of interest. Source can be recombinant or isolated from tissue.	Activity and concentration must be known and consistent. Stability under assay conditions is critical [6] [8].
Substrate	The molecule converted by the enzyme.	High purity. A range of concentrations must be prepared from a stock solution. Use of physiologically relevant substrates is preferred [8].
Detection System	To quantify product formation or substrate depletion (e.g., spectrophotometer, fluorimeter, LC-MS/MS).	Must be specific, sensitive, and allow for rapid, continuous or stopped-point measurement [9].
Assay Buffer	Maintains constant pH and ionic strength.	Choice of buffer (e.g., phosphate, Tris, HEPES) can affect enzyme activity and stability. Should mimic physiological conditions when possible [8].
Cofactors / Cations	Required for activity of many enzymes (e.g., NADH, Mg²⁺).	Must be included at saturating, non-inhibitory concentrations in all reaction mixtures [8].
Human Liver Microsomes	A common in vitro system for studying drug metabolism kinetics.	Contains native cytochrome P450 enzymes and other drug-metabolizing enzymes. Protein content is normalized [9].

Historical Context and Original Derivation

The foundational work of Leonor Michaelis and Maud Leonora Menten was published in their 1913 paper "Die Kinetik der Invertinwirkung," which studied the enzyme invertase catalyzing sucrose hydrolysis into glucose and fructose [11]. Their research was conducted in Berlin, where Menten worked as a research assistant after earning her medical degree. Their experimental goal was to test the hypothesis that enzyme catalysis proceeds through the formation of an enzyme-substrate complex, with the reaction rate proportional to the concentration of this complex [11].

Michaelis and Menten recognized that product inhibition complicated kinetic analysis, a problem previously noted by Victor Henri. To circumvent this, they pioneered the initial velocity measurement approach, following the reaction only during the brief initial period where product influence was negligible [11]. They monitored the invertase-catalyzed reaction at various sucrose concentrations by measuring optical rotation changes over time, tracking reactions to completion. Their data analysis assumed equilibrium binding between sucrose and enzyme, postulating the reaction rate was proportional to enzyme-substrate complex concentration [11].

Surprisingly, Michaelis and Menten's original analysis was more comprehensive than typically recognized. Beyond initial velocity measurements, they fitted full time-course data to integrated rate equations incorporating product inhibition. They derived a single global constant representing all their data—not the Michaelis constant (Kₘ), but rather Vₘₐₓ/Kₘ (the specificity constant multiplied by enzyme concentration) [11]. Their graphical analysis employed an innovative approach: plotting rate versus logarithm of substrate concentration, analogous to Henderson-Hasselbalch equations, rather than using the now-common double reciprocal plot developed later by Lineweaver and Burk [11].

Mathematical Foundations and Core Assumptions

The canonical Michaelis-Menten model describes enzyme kinetics through a fundamental mechanism where enzyme (E) binds substrate (S) to form a complex (ES), which then yields product (P) while regenerating the free enzyme [12]:

The derivation of the Michaelis-Menten equation relies on several critical assumptions that remain essential for proper application of the model [13]:

Assumption 1: No product is present at the reaction start, allowing neglect of the reverse reaction E + P → ES during initial rate measurements [13].

Assumption 2: The steady-state approximation applies, where the rate of ES complex formation equals its rate of breakdown (dissociation plus product formation) [13].

Assumption 3: Enzyme concentration is much lower than substrate concentration ([E] << [S]), ensuring minimal substrate depletion during measurement [13].

Assumption 4: Only initial velocity is measured, maintaining [P] ≈ 0 and [S] approximately constant [13].

Assumption 5: Enzyme exists either as free enzyme or ES complex, with total enzyme concentration [E]ₜ = [E] + [ES] [13].

Under these assumptions, the Michaelis-Menten equation is derived:

Where:

• v = initial reaction velocity
• Vₘₐₓ = maximum velocity (k꜀ₐₜ × [E]ₜ)
• [S] = substrate concentration
• Kₘ = Michaelis constant = (k₋₁ + k꜀ₐₜ)/k₁

The equation produces a rectangular hyperbola where velocity asymptotically approaches Vₘₐₓ as substrate concentration increases [14]. The Kₘ represents the substrate concentration at half-maximal velocity and provides a measure of enzyme-substrate affinity (lower Kₘ indicates higher affinity) [12].

Table 1: Historical vs. Modern Interpretation of Michaelis-Menten Parameters

Parameter	Original 1913 Interpretation	Modern Interpretation	Biological/Experimental Significance
Vₘₐₓ	Maximum velocity of fission during initial phase [11]	Maximum reaction rate at saturating substrate: Vₘₐₓ = k꜀ₐₜ[E]ₜ [12]	Determines enzyme's catalytic capacity; proportional to enzyme concentration
Kₘ	Dissociation constant for enzyme-substrate complex (Kₛ) [11]	Substrate concentration at half-maximal velocity: Kₘ = (k₋₁ + k꜀ₐₜ)/k₁ [12]	Measures apparent enzyme-substrate affinity; lower Kₘ indicates higher affinity
k꜀ₐₜ	Not explicitly defined	Turnover number: molecules converted per active site per unit time [12]	Intrinsic catalytic efficiency of enzyme
Specificity Constant (k꜀ₐₜ/Kₘ)	Global constant derived from full time-course analysis [11]	Measure of catalytic efficiency and specificity for competing substrates [12]	Determines enzyme selectivity under physiological substrate concentrations

Evolution of Parameter Estimation Methods

The methodology for estimating Vₘₐₓ and Kₘ has evolved significantly from Michaelis and Menten's original graphical approach to contemporary computational methods. Their innovative but laborious technique involved plotting reaction velocity against the logarithm of substrate concentration, then normalizing the curve to achieve a specific slope (0.576) at half-maximal velocity to extract parameters [11].

Linear Transformation Methods: The 1934 Lineweaver-Burk double reciprocal plot (1/v vs. 1/[S]) became the standard linearization method for decades, despite its susceptibility to error propagation with imperfect data [11]. Other linear transformations include Eadie-Hofstee (v vs. v/[S]) and Hanes-Woolf ([S]/v vs. [S]) plots, each with different error distribution characteristics [12].

Modern Computational Approaches: Current parameter estimation employs nonlinear regression to directly fit the hyperbolic Michaelis-Menten equation to experimental data, providing more statistically reliable parameter estimates [15]. Bayesian inference methods have emerged as powerful alternatives, particularly when using models derived with the total quasi-steady-state approximation (tQ model) rather than the standard approximation (sQ model) [15]. The tQ model remains accurate under a wider range of conditions, especially when enzyme concentration is not negligible compared to substrate [15].

Optimal Experimental Design: Contemporary research emphasizes designing experiments to maximize parameter identifiability. For progress curve assays, starting with substrate concentrations near Kₘ is recommended, while for initial velocity assays, substrate concentrations should span from well below to well above Kₘ [15]. Recent studies demonstrate that using multiple starting concentrations with limited sampling points can yield reliable parameter estimates comparable to more data-intensive methods [9].

Table 2: Comparative Analysis of Parameter Estimation Methods

Method	Key Principle	Advantages	Limitations	Optimal Use Case
Michaelis-Menten Original (1913)	Rate vs. log[S] plot with normalization to slope 0.576 at v/2 [11]	Comprehensive analysis of full time-course data with product inhibition [11]	Laborious graphical procedure; requires normalization step	Historical interest; understanding original derivation
Lineweaver-Burk (1934)	Double reciprocal plot: 1/v vs. 1/[S] yields linear relationship [11]	Linearization simplifies parameter estimation visually	Error propagation magnifies uncertainties; statistically flawed	Quick visual assessment (though discouraged for final analysis)
Nonlinear Regression	Direct fitting of v = Vₘₐₓ[S]/(Kₘ + [S]) to experimental data	Statistically robust; proper error weighting; no data transformation	Requires computational tools; initial parameter estimates needed	Standard modern approach for accurate parameter estimation
Bayesian Inference with tQ Model	Uses total quasi-steady-state approximation model within Bayesian framework [15]	Accurate even when [E] ≈ [S]; identifies optimal experimental designs	Computationally intensive; requires statistical expertise	Challenging conditions where standard assumptions may not hold

Contemporary Experimental Protocols

Modern enzyme kinetics research employs sophisticated protocols for reliable estimation of Vₘₐₓ and Kₘ, particularly in pharmaceutical applications where these parameters inform drug metabolism predictions.

Initial Velocity Assays: The traditional approach measures initial reaction rates at varying substrate concentrations. Protocols require careful control of conditions (pH, temperature, ionic strength) and use of appropriate detection methods (spectrophotometric, fluorometric, chromatographic) [16]. Each substrate concentration is tested in triplicate with appropriate controls to ensure reliability.

Progress Curve Assays: This approach fits the entire time-course of product formation or substrate depletion to integrated rate equations. Modern implementations use computational fitting to extract parameters from fewer data points. A recent study demonstrated that an optimal design approach using multiple starting concentrations with late sampling points provides reliable estimates of intrinsic clearance (CLᵢₙₜ), Vₘₐₓ, and Kₘ with minimal samples [9].

Specific Protocol for Metabolic Studies: In drug development, enzyme kinetic parameters for cytochrome P450 enzymes are typically determined using human liver microsomes. A validated protocol involves [9]:

• Incubating test compounds at multiple starting concentrations (typically 6-8 concentrations spanning expected Kₘ range)
• Sampling at optimized late time points (reducing number of samples while maintaining information content)
• Analyzing samples via liquid chromatography-tandem mass spectrometry (LC-MS/MS)
• Fitting substrate depletion data to appropriate kinetic models using nonlinear regression

Validation Studies: Comparative studies show that optimal design approaches yield parameter estimates within 2-fold of values obtained from more intensive sampling methods in >90% of cases for CLᵢₙₜ and >80% for Vₘₐₓ and Kₘ [9]. These methods are particularly valuable when assessing potential nonlinear metabolism risks in vivo.

Advanced Applications and Modern Interpretations

Beyond basic enzyme characterization, Michaelis-Menten kinetics finds application in diverse fields with evolving interpretations of Vₘₐₓ and Kₘ.

Drug Discovery and Development: In pharmacokinetics, Kₘ values determine potential nonlinear metabolism at therapeutic concentrations. Drugs administered at doses producing concentrations approaching or exceeding Kₘ may exhibit dose-dependent clearance. Accurate estimation of these parameters enables prediction of in vivo behavior from in vitro data [9].

Microbial Ecology and Systems Biology: Michaelis-Menten parameters describe nutrient uptake in microorganisms, with studies revealing relationships between cell size and kinetic parameters. Research indicates Vₘₐₓ scales with cell surface area (approximately Vₘₐₓ ∝ cell volume²ᐟ³), while Kₘ shows trade-off relationships with Vₘₐₓ [10]. Chemotrophic organisms generally exhibit higher mass-specific Vₘₐₓ and Kₘ values than phototrophs [10].

Single-Molecule Enzymology: Advanced techniques now probe enzyme kinetics at the single-molecule level, revealing heterogeneity and dynamic disorder not apparent in ensemble measurements. These studies sometimes show deviations from classical Michaelis-Menten behavior, prompting development of more sophisticated models.

Limitations and Extensions: The classical equation assumes homogeneity of enzyme populations, absence of allosteric effects, and single-substrate reactions. Extensions include models for multi-substrate reactions, allosteric enzymes (Hill equation), and inhibition patterns (competitive, noncompetitive, uncompetitive). Recent work emphasizes conditions where the standard quasi-steady-state approximation fails and total quasi-steady-state approximation models are required [15].

Table 3: Representative Enzyme Kinetic Parameters Across Biological Systems

Enzyme	Kₘ (M)	k꜀ₐₜ (s⁻¹)	k꜀ₐₜ/Kₘ (M⁻¹s⁻¹)	Biological Context
Chymotrypsin	1.5 × 10⁻²	0.14	9.3	Proteolytic enzyme; intermediate affinity, moderate turnover [12]
Pepsin	3.0 × 10⁻⁴	0.50	1.7 × 10³	Stomach protease; high affinity, moderate turnover [12]
Ribonuclease	7.9 × 10⁻³	7.9 × 10²	1.0 × 10⁵	RNA degradation; moderate affinity, high turnover [12]
Carbonic anhydrase	2.6 × 10⁻²	4.0 × 10⁵	1.5 × 10⁷	CO₂ hydration; moderate affinity, extremely high turnover [12]
Fumarase	5.0 × 10⁻⁶	8.0 × 10²	1.6 × 10⁸	Citric acid cycle; very high affinity, high turnover [12]

The Scientist's Toolkit: Essential Research Reagent Solutions

Table 4: Key Reagents and Materials for Michaelis-Menten Kinetic Studies

Reagent/Material	Function/Purpose	Example/Notes
Purified Enzyme	Catalytic agent whose kinetics are being characterized	Source, purity, and specific activity must be documented; e.g., commercially available invertase [11]
Substrate Solutions	Varied concentrations to establish saturation curve	Prepare in reaction buffer; purity critical; e.g., sucrose solutions for invertase [11]
Reaction Buffer	Maintains optimal pH and ionic conditions	Typically includes pH buffer, salts; e.g., acetate buffer for invertase [11]
Detection System	Monitors reaction progress over time	Spectrophotometer, polarimeter (for optical rotation), fluorometer, or LC-MS/MS [9]
Stop Solution	Halts reaction at precise time points	Acid, base, or inhibitor; timing critical for initial rate measurements
Product Standards	Quantification reference for calibration curves	Pure product for standard curve generation
Inhibition Controls	Validates specificity of observed activity	Specific inhibitors, heat-inactivated enzyme, no-enzyme controls
Microsomal Preparations	Drug metabolism studies (pharmaceutical applications)	Human liver microsomes for cytochrome P450 kinetics [9]
Internal Standards	Mass spectrometry quantification (pharmaceutical applications)	Stable isotope-labeled analogs of analytes; e.g., 5,5-diethyl-1,3-diphenyl-2-imminobarbituric acid [9]

The Michaelis-Menten equation remains a cornerstone of enzymology a century after its introduction, testament to the robustness of its fundamental insights. Michaelis and Menten's original work established not only the mathematical relationship between substrate concentration and reaction velocity but also key experimental approaches including initial velocity measurements and consideration of product inhibition [11].

Modern research continues to refine parameter estimation methods, with Bayesian approaches and optimal experimental designs improving accuracy while reducing experimental burden [9] [15]. The interpretation of Vₘₐₓ and Kₘ has expanded from basic enzyme characterization to applications in drug development, microbial ecology, and systems biology [9] [10].

Future directions include integration of single-molecule observations, development of more comprehensive models for complex enzyme systems, and application of machine learning to kinetic parameter estimation. The enduring relevance of the Michaelis-Menten equation lies in its elegant simplification of complex biochemical processes while providing a framework that can be extended and refined as experimental capabilities advance.

The hyperbolic relationship between substrate concentration and reaction velocity, formalized by the Michaelis-Menten equation, remains a cornerstone for quantifying enzyme behavior and inhibitor interactions in biochemical and pharmacological research [17]. This relationship is described by the equation V₀ = (Vₘₐₓ × [S]) / (Kₘ + [S]), where V₀ is the initial reaction velocity, [S] is the substrate concentration, Vₘₐₓ is the maximum velocity, and Kₘ is the Michaelis constant [18]. Within the broader thesis of Vmax and Km estimation research, precise determination of these parameters is not merely an academic exercise but a critical endeavor with direct implications for understanding metabolic pathways, characterizing drug metabolism, and designing targeted therapies [9]. The half-maximal velocity, defined by the point where V₀ = Vₘₐₓ/2, provides the operational definition of Kₘ, serving as a quantitative measure of an enzyme's apparent affinity for its substrate [17] [19]. This whitepaper provides an in-depth technical guide to interpreting these fundamental kinetic curves and the experimental methodologies employed for robust parameter estimation in contemporary research.

Deconstructing the Hyperbolic Curve: A Graphical Primer

The classic Michaelis-Menten plot graphs reaction velocity (V₀) against substrate concentration ([S]), yielding a characteristic hyperbolic curve [17]. This shape arises from the underlying mechanism of enzyme catalysis, where the formation of an enzyme-substrate (ES) complex is a prerequisite for product formation [20].

Key Graphical Features and Interpretations:

• The Initial Linear Region: At low [S] where [S] << Kₘ, the equation simplifies to V₀ ≈ (Vₘₐₓ/Kₘ)[S]. Velocity increases approximately linearly with [S], indicating that most enzyme active sites are unoccupied. The slope of this region is Vₘₐₓ/Kₘ [20].
• The Curvilinear Transition Region: As [S] approaches and passes Kₘ, the relationship becomes nonlinear. The Kₘ is defined as the substrate concentration at which the reaction velocity is half of Vₘₐₓ [17]. A lower Kₘ value indicates a higher apparent affinity of the enzyme for the substrate, as half-saturation is achieved at a lower substrate concentration [18].
• The Plateau Region (Vₘₐₓ): At high [S] where [S] >> Kₘ, the equation simplifies to V₀ ≈ Vₘₐₓ. The curve asymptotically approaches a maximum velocity, signifying that all available enzyme active sites are saturated with substrate. At this point, the reaction rate is zero-order with respect to substrate and depends solely on enzyme concentration and its intrinsic turnover number (k_cat) [20] [19]. Vₘₐₓ can only be increased by increasing the concentration of active enzyme [18].

It is critical to distinguish this hyperbolic kinetics, typical of Michaelis-Menten enzymes, from sigmoidal kinetics. Sigmoidal curves are characteristic of allosteric enzymes with multiple interacting subunits, where substrate binding at one site increases the affinity of other sites, leading to cooperative behavior [21].

Table 1: Key Parameters Derived from Michaelis-Menten Hyperbolic Curves

Parameter	Symbol	Graphical Determination	Biochemical Meaning	Impact of Higher Value
Maximum Velocity	Vₘₐₓ	The asymptotic plateau of the hyperbola [17].	The maximum reaction rate when enzyme is fully saturated. Limited by k_cat and [Enzyme].	Higher maximum catalytic throughput.
Michaelis Constant	Kₘ	Substrate concentration at Vₘₐₓ/2 [17].	Apparent affinity of enzyme for substrate. Approximates the dissociation constant (Kd) for ES complex when kcat << k_off [18].	Lower apparent substrate affinity.
Catalytic Efficiency	k_cat/Kₘ	Derived parameter; slope of linear region (Vₘₐₓ/Kₘ) [17].	Overall efficiency of an enzyme combining substrate binding (1/Kₘ) and catalysis (k_cat).	More efficient enzyme at low substrate concentrations.
Turnover Number	k_cat	Calculated as Vₘₐₓ / [E_total] [19].	Number of substrate molecules converted to product per enzyme active site per unit time.	Faster conversion of substrate to product at saturation.

Methodologies for Parameter Estimation: From Classic Plots to Modern Assays

Accurate estimation of Vₘₐₓ and Kₘ is foundational. Researchers employ various experimental and analytical strategies, each with strengths and limitations.

Direct Fitting and Linear Transformations

The most straightforward method is to perform nonlinear regression to fit the hyperbolic Michaelis-Menten equation directly to velocity vs. [S] data [15]. Historically, linear transformations like the Lineweaver-Burk plot (double-reciprocal plot: 1/V vs. 1/[S]) were used to visualize data and extract parameters [22].

• Y-intercept = 1/Vₘₐₓ
• X-intercept = -1/Kₘ
• Slope = Kₘ/Vₘₐₓ While useful for illustrative purposes and identifying inhibition types (competitive, non-competitive), these plots can distort experimental error and are less reliable for accurate parameter estimation than direct nonlinear fitting [22].

Progress Curve and Substrate Depletion Assays

Modern approaches often utilize progress curve or substrate depletion assays, which can be more efficient with fewer data points. Instead of measuring initial velocities at multiple substrate concentrations, these methods follow product formation or substrate loss over time from one or several starting concentrations [9] [15].

A significant advancement in this area is the Optimal Design Approach (ODA) evaluated in contemporary research. This method uses multiple starting substrate concentrations (C₀) with strategically chosen late sampling time points (tₛ) [9]. When experimentally evaluated against a reference method (the multiple depletion curves method, MDCM) using human liver microsomes and 30 compounds, the ODA showed strong agreement: >90% of intrinsic clearance (CLᵢₙₜ) estimates and >80% of Vₘₐₓ and Kₘ estimates were within a 2-fold difference [9]. This method is particularly valuable for assessing nonlinear metabolism risk in drug discovery [9].

Table 2: Comparison of Key Methodologies for Vₘₐₓ and Kₘ Estimation

Method	Core Principle	Typical Experimental Design	Key Advantages	Key Limitations/Considerations
Initial Velocity (Classic)	Measures V₀ at a range of fixed [S] points.	Multiple reactions, each at a different [S], measured at early time points [17].	Conceptually simple, directly visualizes hyperbola. Widely understood.	Can be resource-intensive (many samples). Requires careful assurance of initial rate conditions.
Substrate Depletion (Progress Curve)	Fits timecourse of substrate loss to kinetic model.	Monitors [S] over time from one or more starting C₀ [9].	Can be more efficient with fewer data points. Provides estimates of CLᵢₙₜ directly.	Requires an accurate analytical method (e.g., LC-MS/MS). More complex data analysis.
Optimal Design (ODA)	A progress curve method using multiple C₀ with optimized late tₛ.	A limited number of samples taken at strategic late time points from several different C₀ [9].	Efficient with limited samples. Good for identifying nonlinearity risk. Reliable agreement with reference methods [9].	Design requires understanding of expected parameter space.
Bayesian tQ Model Fitting	Uses the total quasi-steady-state approximation (tQSSA) model for fitting.	Fits progress curve data to the more general tQ model (Equation 2) [15].	Accurate even when enzyme concentration is not low ([E] ~ or > [S] or Kₘ). Overcomes bias of standard MM equation in vivo [15].	Computationally more intensive. Requires specialized software/packages.

Advanced Computational: The Bayesian tQ Model

A critical limitation of the standard Michaelis-Menten equation is its requirement that total enzyme concentration [Eₜ] be much lower than Kₘ + [Sₜ] for accuracy [15]. This condition often does not hold in vivo. The total QSSA (tQ) model provides a more robust framework valid over wider concentration ranges [15]. A Bayesian inference approach using this tQ model can yield unbiased estimates of k_cat and Kₘ from progress curve data without restrictive assumptions about enzyme concentration, enabling more accurate in vitro to in vivo extrapolation [15].

Diagram 1: Experimental Workflow for Kinetic Parameter Estimation (85 chars)

Factors Influencing Kinetic Parameters and Experimental Design

Accurate interpretation requires awareness of factors that alter Vₘₐₓ and Kₘ.

• Enzyme Concentration: Vₘₐₓ is directly proportional to the concentration of active enzyme ([E]); doubling [E] doubles Vₘₐₓ. In contrast, Kₘ is theoretically independent of [E], as it is an intensive property of the enzyme-substrate pair [19].
• Temperature and pH: Both affect enzyme structure and activity. They typically alter Vₘₐₓ by changing k_cat and can also affect Kₘ by altering substrate binding affinity. Each enzyme has an optimal temperature and pH [19].
• Inhibitors: The hallmark of different inhibitor types is their distinctive effect on the hyperbolic curve and its linear transformations [22].
  • Competitive Inhibitors: Increase apparent Kₘ; no change to Vₘₐₓ.
  • Non-competitive Inhibitors: Decrease Vₘₐₓ; no change to Kₘ.
  • Uncompetitive Inhibitors: Decrease both Vₘₐₓ and apparent Kₘ.

The Scientist's Toolkit: Essential Reagents and Materials

Table 3: Research Reagent Solutions for Enzyme Kinetic Studies

Reagent/Material	Typical Source/Example	Function in Experiment	Critical Consideration
Recombinant Enzyme or Tissue Fractions	Commercial vendors; Human liver microsomes (HLM) [9].	Source of the enzyme activity being characterized.	Purity, activity lot-to-lot variability, relevance to physiological system (e.g., HLM for cytochrome P450 studies).
Substrate Library	Traditional probe substrates (e.g., midazolam, diclofenac) [9]; new molecular entities.	The molecule whose conversion is measured.	Solubility, specificity for the target enzyme, availability of analytical detection method.
Co-factors	NADPH (for P450s), Mg²⁺, ATP.	Essential for the catalytic activity of many enzymes.	Stability in buffer, required concentration for saturation.
Analytical Detection System	Liquid Chromatography-Tandem Mass Spectrometry (LC-MS/MS) [9].	Quantifies substrate depletion or product formation with high sensitivity and specificity.	Sensitivity, dynamic range, freedom from matrix interference.
Incubation Buffer	Phosphate, Tris, HEPES buffers.	Provides stable pH and ionic environment for the enzymatic reaction.	pH optimum, chemical compatibility with enzyme and substrate.
Internal Standard	Stable isotope-labeled analog of substrate/product [9].	Added to samples prior to analysis to correct for variations in sample processing and instrument response.	Should be chemically identical to analyte except for mass label.
Inhibitors/Activators	Chemical inhibitors, monoclonal antibodies.	Used to characterize enzyme selectivity or mechanism.	Specificity, potency, solubility.

Diagram 2: Enzyme Kinetic Reaction Mechanism (63 chars)

Advanced Considerations and Future Directions

The field of enzyme kinetics is moving beyond simple Michaelis-Menten analysis. Key frontiers include:

• In Vivo Kinetics: Recognizing that intracellular enzyme concentrations can be high, invalidating the standard Michaelis-Menten assumption. The tQSSA and Bayesian approaches are crucial for bridging in vitro and in vivo data [15].
• Parameter Identifiability: A major challenge is that parameters k_cat and Kₘ can be highly correlated in progress curve fits, leading to uncertainty. Optimal experimental design (like ODA) and advanced statistical inference are required to ensure reliable, unique estimates [9] [15].
• Automation and High-Throughput: In drug discovery, methods must balance thoroughness with resource constraints. Efficient designs like the ODA that use a limited number of samples are increasingly valuable for early-stage compound profiling [9].

Diagram 3: Pathways from Data to Kinetic Parameters (77 chars)

Interpreting the hyperbolic velocity-substrate curve and its defining parameter, the half-maximal velocity (Kₘ), is fundamental to quantitative biochemistry and pharmacology. While the Michaelis-Menten framework provides an essential model, contemporary research demands more sophisticated methodologies like substrate depletion assays, optimal experimental design (ODA), and Bayesian fitting with the tQ model to address challenges of parameter identifiability and in vivo extrapolation [9] [15]. For researchers and drug development professionals, selecting the appropriate experimental and analytical strategy is critical for generating reliable kinetic parameters that accurately predict enzyme behavior in complex biological systems, ultimately guiding the development of safer and more effective therapeutics.

The Role of the Enzyme-Substrate Complex and the Steady-State Assumption in Kinetic Theory

1. Introduction: The Foundation of Enzyme Kinetics in Modern Research

The quantitative analysis of enzyme catalysis, centered on the accurate estimation of the kinetic parameters Vmax (maximum velocity) and Km (Michaelis constant), is a cornerstone of biochemistry, pharmacology, and drug development. These parameters are not abstract numbers; they provide a rigorous, quantitative framework for understanding molecular efficiency, substrate affinity, and inhibitor potency. This understanding is predicated on two interconnected conceptual pillars: the formation of the enzyme-substrate (ES) complex as the central catalytic intermediate and the steady-state assumption that allows this dynamic process to be described by a workable mathematical model. The Michaelis-Menten equation, derived from these concepts, remains the fundamental model for characterizing enzyme activity [12] [5]. The ongoing refinement of Vmax and Km estimation methodologies, from classical linearizations to modern nonlinear regression and computational simulations, represents the practical application of this theory. This guide examines the structural and kinetic principles of the ES complex, details the derivation and implications of the steady-state assumption, and frames this classical theory within the context of contemporary, high-precision parameter estimation research essential for drug discovery and enzyme engineering.

2. The Enzyme-Substrate Complex: Structural and Energetic Basis of Catalysis

The enzyme-substrate complex is the transient, high-energy intermediate in which the substrate is converted to product. Its formation and properties are the structural determinants of Km and Vmax.

• Active Site Architecture and Specificity: The active site is a specialized three-dimensional pocket within the enzyme where catalysis occurs. It is composed of amino acid residues that create a unique chemical environment (e.g., hydrophobic, charged, acidic) complementary to the transition state of the reaction [23] [24]. This complementarity is dynamic. The historical "lock-and-key" model has been largely supplanted by the induced fit model, where substrate binding induces conformational changes in the enzyme to achieve an optimal catalytic alignment [23] [25]. This precise arrangement is crucial for the kinetic parameter of specificity (kcat/Km).

• Mechanisms of Catalysis within the Complex: The active site employs several strategies to lower the activation energy of the reaction [25]:

  • Covalent Catalysis: Transient formation of a covalent bond between the enzyme and substrate.
  • General Acid-Base Catalysis: Amino acid residues donate or accept protons.
  • Catalysis by Approximation: Binding brings two substrates into close proximity and optimal orientation.
  • Metal Ion Catalysis: Bound metal ions stabilize charges, mediate redox reactions, or enhance nucleophilicity. These mechanisms are optimized within the ES complex to maximize kcat, the catalytic rate constant directly related to Vmax (Vmax = kcat [E]total).

• Modern Structural Analysis: Contemporary techniques like cryo-electron microscopy (cryo-EM) and molecular dynamics (MD) simulations now allow researchers to visualize and simulate the dynamic conformational states (open, intermediate, closed) of the ES complex, linking structural flexibility directly to substrate capture and catalytic efficiency [24] [26]. This provides a physical basis for understanding kinetic parameters.

3. The Steady-State Assumption and the Derivation of Michaelis-Menten Kinetics

The kinetic behavior of the ES complex is described by the Michaelis-Menten model. For the reversible reaction: E + S ⇌ ES → E + P The key challenge is solving for the rate of product formation (v) as a function of substrate concentration [S].

• The Steady-State Assumption: In 1925, Briggs and Haldane introduced a critical simplification [27]. They proposed that after a brief initial transient, the concentration of the ES complex remains constant over time because the rate of its formation equals the rate of its breakdown (to product + enzyme or back to substrate + enzyme). This is expressed as d[ES]/dt = 0. This assumption is valid when the total enzyme concentration [E]_total is much lower than [S], a condition typical in experimental setups [27] [5].

• Derivation of the Michaelis-Menten Equation: Applying the steady-state assumption and mass conservation ([E]total = [E]free + [ES]), the rate equation simplifies to: v = (Vmax * [S]) / (Km + [S]) Here, Vmax (kcat * [E]_total) is the maximum theoretical rate at saturating [S], and Km (the Michaelis constant) is the substrate concentration at which v = Vmax/2 [12] [5]. Km is an aggregate constant approximating the enzyme's affinity for the substrate; a lower Km generally indicates higher affinity.

• Graphical Representation and Meaning of Parameters: The plot of v vs. [S] is a rectangular hyperbola. At low [S] ([S] << Km), the reaction is first-order with respect to [S], and v is approximated by (Vmax/Km)[S]. The specificity constant kcat/Km is the critical measure of catalytic efficiency under these conditions [12]. At high [S] ([S] >> Km), the reaction rate approaches Vmax (zero-order in [S]), and the enzyme is saturated.

Table 1: Representative Michaelis-Menten Parameters for Enzymes [12]

Enzyme	Km (M)	kcat (s⁻¹)	kcat/Km (M⁻¹s⁻¹)	Catalytic Efficiency Implication
Chymotrypsin	1.5 × 10⁻²	0.14	9.3	Moderate efficiency
Carbonic anhydrase	2.6 × 10⁻²	4.0 × 10⁵	1.5 × 10⁷	Extremely high efficiency (diffusion-limited)
Fumarase	5.0 × 10⁻⁶	8.0 × 10²	1.6 × 10⁸	Very high affinity and efficiency

4. Experimental Determination of Vmax and Km: Methodologies and Best Practices

Accurate estimation of Vmax and Km is critical for reliable biochemical characterization. Methods have evolved from linear transformations to more robust nonlinear techniques.

• Classical Linear Transformation Methods: These involve algebraically manipulating the Michaelis-Menten equation to generate linear plots.

  • Lineweaver-Burk (Double-Reciprocal) Plot: 1/v vs. 1/[S]. While historically widespread, it is statistically flawed as it distorts experimental error, giving undue weight to low-velocity data points [28].
  • Eadie-Hofstee Plot: v vs. v/[S]. Less prone to error distortion than Lineweaver-Burk but still inferior to direct nonlinear fitting [28].

• Modern Nonlinear Regression (NLR): The preferred method is to fit the untransformed velocity (v) vs. substrate concentration ([S]) data directly to the hyperbolic Michaelis-Menten equation using iterative computational algorithms (e.g., in GraphPad Prism, NONMEM) [28]. This method treats all data points with appropriate weighting and yields the most accurate and precise estimates of Vmax and Km with associated confidence intervals.

• Full Time-Course Analysis (NM Method): The most advanced approach fits the raw time-course data of substrate depletion or product formation to the integrated form of the Michaelis-Menten equation [28]. This method, often using powerful software like NONMEM, utilizes all data points without requiring the estimation of initial velocities, further improving parameter accuracy, especially with complex error structures.

Table 2: Comparison of Vmax and Km Estimation Methods [28]

Estimation Method	Data Transformation	Key Advantage	Key Disadvantage	Relative Accuracy/Precision
Lineweaver-Burk (LB)	1/v vs. 1/[S]	Simple visualization of inhibition type	Severe error distortion; poor parameter reliability	Low
Eadie-Hofstee (EH)	v vs. v/[S]	Less error distortion than LB	Error not uniform; suboptimal for statistical inference	Moderate
Nonlinear Regression (NL)	v vs. [S] (direct fit)	Proper error weighting; statistically sound	Requires computational software	High
Full Time-Course (NM)	[S] vs. time (integrated fit)	Uses all data; no initial velocity approximation	Requires sophisticated software and modeling expertise	Highest

5. Advanced Protocols: From Structural Biology to Computational Prediction

• Protocol 1: Structural Characterization of the ES Complex via Crystallography/cryo-EM.

  • Sample Preparation: Purify the target enzyme to homogeneity. For crystallography, generate a high-concentration protein solution and screen crystallization conditions with and without substrate or a non-reactive substrate analogue [24]. For cryo-EM, vitrify the sample in a thin layer of ice [26].
  • Data Collection & Modeling: Collect X-ray diffraction or cryo-EM images. Solve the phase problem (crystallography) or perform 3D reconstruction (cryo-EM). Dock the substrate into the active site electron density, which may require computational modeling if a true substrate complex is not captured [24].
  • MD Simulation Refinement: Use the solved structure as a starting point for molecular dynamics simulations in explicit solvent to model the dynamic behavior and conformational sampling of the ES complex under physiological conditions [24] [26].

• Protocol 2: Kinetic Parameter Estimation via Nonlinear Regression.

  • Experimental Data Collection: Perform initial velocity experiments. Hold enzyme concentration constant and measure initial velocity (v) across a wide range of substrate concentrations [S] (spanning ~0.2–5 x Km). Use sensitive, continuous assays where possible.
  • Data Preparation: Input paired [S] and v data into statistical software, ensuring v values have appropriate error estimates (e.g., standard deviation from replicates).
  • Model Fitting: Fit the data to the model v = (Vmax * [S]) / (Km + [S]). Use appropriate weighting (e.g., 1/variance). Estimate parameters by least-squares minimization.
  • Validation: Assess goodness-of-fit (R², residual plot). Report Vmax and Km with 95% confidence intervals. Compare models if testing for inhibition (competitive, non-competitive) [28].

• Protocol 3: In silico Prediction of Substrate Specificity and Kinetics.

  • Model Training: As demonstrated by AI tools like EZSpecificity, train a graph neural network on a comprehensive database of known enzyme structures (or sequences) and their validated substrates [29].
  • Feature Encoding: Represent the enzyme active site and candidate substrate molecules as graphs, encoding atomic properties, bonds, and spatial relationships [29].
  • Prediction & Validation: The model outputs a prediction of catalytic compatibility or a quantitative activity score. These computational hits must be validated experimentally through targeted kinetic assays [30] [29].

The Scientist's Toolkit: Essential Reagents and Resources

Item/Category	Function/Application	Example/Note
Purified Target Enzyme	The catalyst under investigation. Must be highly pure and active.	Recombinantly expressed and affinity-purified protein.
Substrates & Analogues	To measure activity and, for analogues, to trap the ES complex for structural studies.	Natural physiological substrate; unreactive transition-state analogues (e.g., phosphonates).
Cofactors & Cations	Required for the activity of many enzymes (metalloenzymes, dehydrogenases).	Mg²⁺, Zn²⁺, NADH, ATP. Concentration must be optimized and held constant in assays.
Detection Reagents	To quantify substrate loss or product formation continuously or at endpoint.	Chromogenic/fluorogenic probes, coupled enzyme systems, HPLC-MS standards.
Crystallization/Cryo-EM Kits	To generate ordered arrays (crystals) or vitrified samples for structural analysis.	Sparse matrix screens; graphene oxide grids for cryo-EM [26].
Kinetic Analysis Software	To fit data, estimate parameters, and perform statistical analysis.	GraphPad Prism, SigmaPlot; NONMEM for advanced population kinetic modeling [28].
Computational Suites	For MD simulations, molecular docking, and AI/ML-based prediction.	CHARMM/NAMD (MD) [24]; AutoDock (docking); EZSpecificity models (specificity prediction) [29].

6. Future Directions: AI, Dynamics, and the Expansion of Kinetic Theory

The field is moving beyond static measurements of Km and Vmax. Artificial Intelligence (AI) and machine learning (ML) are revolutionizing enzyme science. Models like EZSpecificity can predict substrate specificity from sequence or structure, guiding enzyme engineering and the discovery of biocatalysts for novel reactions [30] [29]. This integrates directly with directed evolution, where AI models can predict fitness landscapes, dramatically accelerating the optimization of kcat and Km [30]. Furthermore, techniques like cryo-EM are revealing that enzymes are not static locks but dynamic machines; the distribution of conformational states influences the macroscopic kinetic parameters [26]. Future kinetic models may incorporate these dynamic ensembles, leading to a more nuanced understanding of catalysis that bridges structural biology, computational prediction, and high-precision kinetic parameter estimation.

Visualization: Enzyme Catalysis Mechanism and Kinetic Analysis

Experimental Approaches and Analytical Methods for Vmax and Km Determination

Accurate estimation of the kinetic parameters Vmax (maximum reaction velocity) and Km (Michaelis constant) forms the cornerstone of quantitative enzymology and is critical in drug discovery, where enzymes constitute a major class of therapeutic targets [31]. These parameters are not mere numbers; they are fundamental descriptors of enzyme function, defining catalytic efficiency and substrate affinity. Their precise determination is essential for characterizing enzyme mechanisms, diagnosing metabolic disorders, and evaluating the potency and modality of inhibitory compounds.

This guide details the core experimental methodologies—initial velocity assays and progress curve analysis—within the rigorous framework required for reliable parameter estimation. A common pitfall in kinetic research is the generation of precise but inaccurate parameters due to flawed experimental design. This often stems from incorrect substrate concentration ranges, misapplication of the Michaelis-Menten equation under non-valid conditions, or improper analysis of reaction time courses [32] [33]. The following sections provide a technical roadmap for designing experiments that yield kinetically meaningful and reproducible estimates of Km and Vmax, ensuring data integrity for downstream applications in hit validation and structure-activity relationship (SAR) studies [31].

Foundational Concepts and Experimental Prerequisites

The Critical Importance of Initial Velocity Conditions

The Michaelis-Menten equation (v = (Vmax * [S]) / (Km + [S])) is derived under steady-state assumptions, which are only valid when measuring the initial velocity of a reaction. An initial velocity is defined as the rate measured in the initial linear phase where less than 10% of the substrate has been converted to product [31]. Adhering to this condition is non-negotiable for several reasons:

• It ensures the substrate concentration ([S]) is essentially constant and equal to the starting concentration.
• It negates significant effects from product inhibition, substrate depletion, and the reverse reaction.
• It guarantees the reaction velocity is directly proportional to the enzyme concentration [31].

Failure to operate under initial velocity conditions leads to non-linear progress curves, an undefined and decreasing [S], and invalidates the steady-state kinetic treatment, rendering subsequent Km and Vmax estimates erroneous [31].

The Relationship Between Enzyme Concentration and Parameter Validity

A fundamental yet frequently overlooked criterion is the requirement for the total enzyme concentration ([E]₀) to be significantly lower than the Km. Recent rigorous analysis demonstrates that the classic Michaelis-Menten equation is only valid for reliably estimating both Km and Vmax when [E]₀ ≤ 0.01Km [33]. At higher enzyme concentrations (0.01Km < [E]₀ < Km), the reaction dynamics deviate, and a more complex equation is required. Operating with [E]₀ approaching or exceeding Km introduces significant systematic error into parameter estimates [33]. Therefore, a key step in assay development is empirically determining the dilute enzyme concentration that yields a linear progress curve for the assay duration while satisfying this stringent concentration criterion.

Defining the Optimal Substrate Concentration Range

Selecting the correct substrate concentrations is paramount for robust parameter estimation. The goal is to define a range that adequately captures the transition from first-order to zero-order kinetics.

• Minimum Range: A minimum of six substrate concentrations is recommended for an initial estimate [31].
• Optimal Range: For reliable fitting, use 8 or more substrate concentrations spanning from below to above the Km [31].
• Ideal Span: Concentrations should ideally cover 0.2Km to 5.0Km [31]. This range ensures sufficient data points in the sensitive, approximately linear region below Km and in the saturation region approaching Vmax.

For competitive inhibitor screening, the assay must be run with a substrate concentration at or below the Km value. Using [S] >> Km dramatically reduces the assay's sensitivity for detecting this important class of inhibitors [31].

Table 1: Guidelines for Key Experimental Parameters in Kinetic Assays

Parameter	Optimal Value or Range	Rationale & Consequences of Deviation
Substrate Depletion	< 10%	Maintains [S] ~constant; >10% leads to non-linearity and invalid steady-state assumptions [31].
[E]₀ / Km Ratio	≤ 0.01	Ensures validity of Michaelis-Menten equation for simultaneous Km & Vmax estimation [33].
Substrate Concentration Range	0.2Km – 5.0Km	Adequately characterizes hyperbolic saturation curve [31].
Number of [S] Data Points	≥ 8	Enables robust non-linear regression fitting [31].
Assay [S] for Inhibitor Screening	≤ Km	Maximizes sensitivity for identifying competitive inhibitors [31].

Diagram 1: Kinetic Assay Development & Analysis Workflow

Core Experimental Methodologies

Initial Velocity Assays: Protocol and Best Practices

This method involves running separate reactions at different substrate concentrations and measuring the velocity at a single early time point for each.

Detailed Protocol:

• Reagent Preparation: Prepare a master reaction buffer containing all necessary components (cofactors, salts, pH buffer). Separately, prepare a serial dilution of the substrate to generate at least 8 concentrations spanning the target range (e.g., 0.2–5.0 × estimated Km).
• Initiation: In a plate or cuvette, mix a fixed, dilute volume of enzyme solution with the reaction buffer. Initiate the reaction by adding the substrate solution. The final enzyme concentration must be validated to satisfy [E]₀ ≤ 0.01Km [33].
• Measurement: Immediately begin monitoring the increase in product (or decrease in substrate) using an appropriate detection method (e.g., absorbance, fluorescence). The signal must be confirmed to be linear with product concentration over the assay's range [31].
• Data Capture: Record the signal at short, regular intervals (e.g., every 10-30 seconds) for a period that captures only the initial linear phase. The duration of linearity must be pre-determined from a progress curve experiment.
• Control Measurements: Include negative controls lacking enzyme or substrate to correct for background signal [31].
• Velocity Calculation: For each substrate concentration, calculate the initial velocity (v₀) as the slope of the linear portion of the progress curve (signal vs. time).

Progress Curve Analysis: Protocol and Best Practices

This method obtains multiple data points from a single reaction by continuously monitoring product formation over time, fitting the entire curve to an integrated rate equation.

Detailed Protocol:

• Reagent Preparation: Similar to the initial velocity assay, prepare reaction buffer and substrate solution. Critical Requirement: For progress curve analysis, a single substrate concentration is insufficient to uniquely determine Km and kcat (k₂). Experiments must be performed at multiple starting substrate concentrations ([S]₀) to allow proper parameter identification [32].
• Reaction Initiation & Monitoring: Mix enzyme and substrate to start the reaction. Use a continuous detection method to collect signal data points at high frequency from the start of the reaction until it approaches completion or a clear plateau.
• Data Requirements: Collect dense time-course data for each [S]₀. The experiment must be designed such that the signal remains within the detection system's linear range throughout [31].

Mathematical Foundation: For the simple irreversible reaction E + S → ES → E + P, the progress curve is described by the integrated equation: t = (P/(k₂[E]₀)) + (Km/(k₂[E]₀)) * ln([S]₀/([S]₀ - P)) [32], where P is product concentration at time t. Since this function cannot be explicitly solved for P, analysis requires non-linear fitting using specialized software.

Diagram 2: Progress Curve Analysis via Numerical Integration

Data Analysis and Parameter Estimation

Analyzing Initial Velocity Data

• Plotting: Plot the calculated initial velocity (v₀) against the corresponding substrate concentration ([S]).
• Non-Linear Regression: Fit the data directly to the Michaelis-Menten equation using non-linear regression (e.g., in GraphPad Prism, SigmaPlot). This is the preferred method as it provides unbiased estimates of Vmax and Km.
• Linear Transformations (Caution): Transformations like Lineweaver-Burk (1/v vs. 1/[S]), Eadie-Hofstee, or Hanes-Woolf can be used for visualization but should not be used for primary parameter estimation. These transformations distort the error structure of the data and can give misleading results.

Analyzing Progress Curve Data

The analysis of full progress curves is computationally intensive and requires specialized tools. Two primary approaches exist [34]:

• Analytical Integration Approach: Uses the implicit integrated rate equation (like the one shown in Section 3.2). Software (e.g., some functions in Prism) can perform the non-linear fit of P(t) to this integrated form.
• Numerical Integration Approach: More flexible for complex mechanisms. Software tools like FITSIM or DYNAFIT allow the user to define a reaction mechanism with differential equations [32]. The program then simulates progress curves by numerically integrating these equations, iteratively adjusting rate constants until the sum of squared differences between simulated and experimental data is minimized [32].

Critical Consideration: A major pitfall is attempting to derive all individual rate constants (k₁, k₋₁, k₂) from a simple product formation curve. Different combinations of these constants can produce identical progress curves, making their unique identification impossible without additional experimental data [32]. The reliably determinable parameters from a standard progress curve are the composite constants Km and kcat (k₂).

Assessing Parameter Reliability: Monte Carlo Simulation

Given the complexity of progress curve fitting, assessing parameter uncertainty is crucial. Monte Carlo simulation is a powerful diagnostic tool for this purpose [32]. The process involves:

• Taking the best-fit curve and the observed variance of the experimental data.
• Generating thousands of synthetic "virtual" datasets by randomly perturbing the best-fit data points within the expected noise distribution.
• Refitting each synthetic dataset.
• Analyzing the distribution of the resulting parameter estimates to generate robust confidence intervals (e.g., 95% CI for Km and Vmax).

This method reveals whether the experimental design yields well-constrained, unique parameter estimates or if the parameters are highly correlated and uncertain [32].

Table 2: Comparison of Kinetic Analysis Methods

Feature	Initial Velocity Assay	Progress Curve Analysis
Experimental Effort	High (many separate reactions)	Lower (fewer reactions, continuous monitoring) [34].
Data Yield per Reaction	Single v₀ data point	Dozens of [P] vs. time points.
Mathematical Analysis	Simpler (direct or linear fit).	Complex (numerical integration & non-linear fitting) [32] [34].
Ability to Detect	Ideal for: Steady-state parameters (Km, Vmax).	Ideal for: Time-dependent phenomena (e.g., slow-binding inhibition, enzyme instability) [31].
Key Pitfall	Missing non-linearity; using invalid [E]₀ [31] [33].	Underdetermined systems; fitting too many parameters [32].
Best for	Routine characterization; inhibitor screening.	Mechanistic studies; detailed characterization.

The Scientist's Toolkit: Essential Reagents and Materials

Table 3: Essential Research Reagent Solutions for Kinetic Assays

Item	Function & Importance	Key Considerations
High-Purity Enzyme	The catalyst of interest. Source (recombinant, native), purity, and specific activity must be known and consistent [31].	Test for contaminating activities. Aliquot and store to maintain stability. Determine lot-to-lot consistency [31].
Defined Substrate	The molecule transformed by the enzyme. Can be the natural substrate or a synthetic surrogate [31].	Purity is critical. Must have a reliable detection method for its depletion or product formation. Ensure adequate supply for entire project [31].
Appropriate Cofactors	Molecules required for enzyme activity (e.g., metals, ATP, NADH).	Identify all essential cofactors from literature. Include at saturating concentrations in assays unless being studied as a variable substrate [31].
Optimized Assay Buffer	Maintains constant pH and ionic strength, and provides optimal enzyme activity/stability.	Includes pH buffer, salts, potential stabilizing agents (e.g., BSA, glycerol). Must not interfere with detection [31].
Validated Control Inhibitors	Known inhibitors (e.g., for kinases: staurosporine) used as assay controls.	Essential for validating assay performance and sensitivity during development and screening [31].
Detection System Components	Enables quantification of reaction progress (e.g., fluorescent probe, coupled enzyme system, radioactive label).	Signal must be linear with product concentration over the entire assay range. Throughput, cost, and sensitivity should match project goals [31].
Inactive Enzyme Mutant	Protein purified identically to wild-type but lacks catalytic activity.	Serves as the highest-quality negative control to identify non-enzymatic background signals [31].

Theoretical Foundations of Enzyme Kinetics and Parameter Estimation

The quantitative analysis of enzyme catalysis centers on determining two fundamental kinetic parameters: the maximum reaction velocity (Vmax) and the Michaelis constant (Km). Vmax represents the theoretical maximum rate of the reaction when the enzyme is fully saturated with substrate, while Km indicates the substrate concentration at which the reaction rate is half of Vmax, providing a measure of the enzyme's affinity for its substrate [22]. These parameters are traditionally derived from the Michaelis-Menten equation, which describes the hyperbolic relationship between substrate concentration and initial reaction velocity [20].

The classical linear transformation methods were developed to overcome the challenge of directly estimating Vmax and Km from the hyperbolic curve. By algebraically manipulating the Michaelis-Menten equation, these methods transform the data into linear forms, allowing for parameter estimation through linear regression. This approach dominated enzyme kinetics for decades before the widespread availability of non-linear regression software [35].

Within the broader thesis on Vmax and Km estimation research, these linear transformations represent the foundational methodologies that enabled the systematic study of enzyme behavior, inhibition mechanisms, and substrate specificity. Their development marked a critical transition from qualitative to quantitative enzymology, establishing standards for kinetic characterization that remain relevant despite advances in computational fitting methods [36].

The Michaelis-Menten Framework and Transformation Principles

The Michaelis-Menten equation, v = (Vmax × [S]) / (Km + [S]), where v is the initial velocity and [S] is the substrate concentration, forms the basis for all three linear transformation methods [20]. This equation arises from the fundamental enzyme kinetic mechanism involving substrate binding, formation of an enzyme-substrate complex, and product release [36].

The linear transformations work by rearranging this equation into forms that yield straight lines when appropriate variables are plotted. Each transformation distributes experimental error differently and provides unique visual insights into the kinetic data. The common objective is to obtain accurate estimates of Vmax and Km through graphical methods that were more accessible before computational approaches became widespread [35].

Table 1: Fundamental Equations of Linear Transformations

Plot Type	Linear Equation Form	X-axis Variable	Y-axis Variable	Slope	Y-intercept	X-intercept
Lineweaver-Burk	1/v = (Km/Vmax)×(1/[S]) + 1/Vmax	1/[S]	1/v	Km/Vmax	1/Vmax	-1/Km
Eadie-Hofstee	v = Vmax - Km×(v/[S])	v/[S]	v	-Km	Vmax	Vmax/Km
Hanes-Woolf	[S]/v = (1/Vmax)×[S] + Km/Vmax	[S]	[S]/v	1/Vmax	Km/Vmax	-Km

Lineweaver-Burk (Double Reciprocal) Plot

Mathematical Derivation and Graphical Interpretation

The Lineweaver-Burk plot, introduced in 1934, is created by taking the reciprocal of both sides of the Michaelis-Menten equation, resulting in the linear form: 1/v = (Km/Vmax) × (1/[S]) + 1/Vmax [35]. This transformation yields a straight line when 1/v is plotted against 1/[S].

On the Lineweaver-Burk plot, the y-intercept corresponds to 1/Vmax, allowing direct determination of the maximum velocity. The x-intercept equals -1/Km, from which Km can be calculated. The slope of the line represents Km/Vmax [22] [37]. This plot gained widespread adoption due to the ease of determining both parameters from intercepts rather than slopes, which was considered advantageous for manual graphical analysis.

Applications in Inhibition Studies

The Lineweaver-Burk plot became particularly valuable for distinguishing different types of enzyme inhibition:

• Competitive inhibition: Increases the apparent Km without affecting Vmax, resulting in lines that intersect on the y-axis [35].
• Pure non-competitive inhibition: Decreases Vmax without altering Km, producing lines that intersect on the x-axis [35].
• Uncompetitive inhibition: Decreases both Vmax and apparent Km, yielding parallel lines [35].
• Mixed inhibition: Affects both Vmax and Km, creating lines that intersect in the second quadrant [35].

This diagnostic capability made the Lineweaver-Burk plot an essential tool for mechanistic studies in enzymology and drug development, where understanding inhibition patterns is crucial for therapeutic design [22].

Limitations and Error Considerations

Despite its historical popularity, the Lineweaver-Burk plot has significant statistical limitations. The reciprocal transformation distorts experimental error, giving disproportionate weight to measurements at low substrate concentrations where the relative error in 1/v is largest [35]. As noted in the literature, "if v = 1 ± 0.1 then 1/v = 1 ± 0.1, a 10% error. However, if v = 10 ± 0.1 then 1/v = 0.1 ± 0.001, only a 1% error" [35]. This uneven error distribution can lead to biased parameter estimates, particularly when data points are unevenly distributed across the substrate concentration range.

Eadie-Hofstee Plot

Mathematical Derivation and Graphical Interpretation

The Eadie-Hofstee plot uses the transformation v = Vmax - Km×(v/[S]), derived by multiplying both sides of the Michaelis-Menten equation by (Km + [S]), rearranging to isolate v on one side [38]. In this plot, v is plotted against v/[S], yielding a straight line with a slope of -Km and a y-intercept of Vmax.

An alternative form, sometimes called the Eadie plot, reverses the axes: v/[S] = (Vmax/Km) - (1/Km)×v, where the slope is -1/Km and the y-intercept is Vmax/Km [38]. This plot is mathematically equivalent to the Scatchard plot used in receptor-binding studies.

Advantages in Error Distribution

Unlike the Lineweaver-Burk transformation, the Eadie-Hofstee plot avoids taking reciprocals of the measured velocity, resulting in more uniform error distribution across the data range [39]. Experimental error is typically assumed to affect the rate v rather than the substrate concentration a, and since v appears on both axes, the errors are correlated [38]. This correlated error structure makes the Eadie-Hofstee plot less sensitive to experimental scatter than the Lineweaver-Burk plot.

Additionally, because the ordinate spans the entire theoretical range of v (from 0 to Vmax), the Eadie-Hofstee plot makes it easier to visually identify data points that deviate significantly from expected behavior, potentially revealing faults in experimental design or assumptions [38].

Historical Context and Attribution

The transformation underlying the Eadie-Hofstee plot has a complex history of independent discovery. Although commonly associated with Eadie (1942) and Hofstee (1959), the linear form was originally credited to Woolf by Haldane and Stern in 1932 [38]. Haldane later clarified in 1957 that "Woolf pointed out that linear graphs are obtained when v is plotted against v×[S]⁻¹, v⁻¹ against [S]⁻¹, or v⁻¹×[S] against [S], the first plot being most convenient unless inhibition is being studied" [38].

The plot is occasionally attributed to Augustinsson (1948), though he did not explicitly cite the earlier work of Haldane, Woolf, or Eadie when introducing the v versus v/[S] plot [38]. This multiplicity of attribution reflects the independent mathematical derivation of this transformation by multiple researchers.

Hanes-Woolf Plot

Mathematical Derivation and Graphical Interpretation

The Hanes-Woolf plot utilizes the transformation [S]/v = (1/Vmax)×[S] + Km/Vmax, derived by multiplying both sides of the Lineweaver-Burk equation by [S] [40]. This yields a linear relationship when [S]/v is plotted against [S].

In this plot, the slope equals 1/Vmax, allowing direct calculation of Vmax. The y-intercept is Km/Vmax, from which Km can be derived using the already determined Vmax value. Alternatively, the x-intercept is -Km [40]. This plot is particularly useful when studying allosteric enzymes, as it can clearly display changes in reaction velocity under varying substrate concentrations [40].

Statistical Advantages

The Hanes-Woolf plot offers superior statistical properties compared to the Lineweaver-Burk plot. Unlike the double-reciprocal transformation, the Hanes-Woolf plot does not disproportionately amplify errors at low substrate concentrations [40]. The transformation results in more evenly distributed errors across the data range, leading to more reliable parameter estimates through linear regression.

Comparative studies have shown that the Hanes-Woolf plot generally provides more accurate estimates of Vmax and Km than the Lineweaver-Burk plot, especially when data quality is variable or when substrate concentrations span limited ranges [40]. This advantage made it preferable for many practical applications despite the slightly more complex parameter extraction (requiring both slope and intercept rather than just intercepts).

Applications in Modern Analysis

While all linear transformation methods have been largely superseded by nonlinear regression for primary parameter estimation, the Hanes-Woolf plot retains value for diagnostic purposes. Its linear representation makes it easier to visually assess data quality, identify outliers, and detect deviations from Michaelis-Menten behavior that might indicate cooperativity, substrate inhibition, or other complex kinetic phenomena [40].

Comparative Analysis of Linear Transformation Methods

Table 2: Comprehensive Comparison of Linear Transformation Methods

Characteristic	Lineweaver-Burk Plot	Eadie-Hofstee Plot	Hanes-Woolf Plot
Linear Equation	1/v = (Km/Vmax)×(1/[S]) + 1/Vmax	v = Vmax - Km×(v/[S])	[S]/v = (1/Vmax)×[S] + Km/Vmax
X-axis Variable	1/[S]	v/[S]	[S]
Y-axis Variable	1/v	v	[S]/v
Slope	Km/Vmax	-Km	1/Vmax
Y-intercept	1/Vmax	Vmax	Km/Vmax
X-intercept	-1/Km	Vmax/Km	-Km
Primary Vmax Determination	From y-intercept: Vmax = 1/(y-int)	Direct from y-intercept	From slope: Vmax = 1/slope
Primary Km Determination	From x-intercept: Km = -1/(x-int)	From slope: Km = -slope	From y-intercept: Km = (y-int)×Vmax
Error Distribution	Highly uneven; amplifies errors at low [S]	Moderately uneven; correlated errors	Most even among the three
Visual Diagnostic Value	Excellent for inhibition studies	Good for identifying outliers	Good for assessing data quality
Historical Usage	Most widespread historically	Less common, valued by specialists	Intermediate popularity
Computational Preference	Least recommended	Intermediate	Most recommended of linear methods

Table 3: Impact on Parameter Estimation Accuracy

Error Condition	Lineweaver-Burk Performance	Eadie-Hofstee Performance	Hanes-Woolf Performance
Low substrate concentration errors	Severely amplified	Moderately affected	Minimally affected
High substrate concentration errors	Minimized	Moderately affected	Moderately affected
Uniform velocity errors	Becomes non-uniform after transformation	Remains correlated across axes	Becomes slightly non-uniform
Small sample sizes	Poor performance due to error amplification	Moderate performance	Best performance among linear methods
Data point distribution	Requires careful spacing, especially at low [S]	Tolerates uneven spacing better	Tolerates uneven spacing well

Modern Experimental Protocols for Kinetic Parameter Estimation

Optimized Experimental Design

Contemporary research emphasizes optimized experimental designs that maximize information content while minimizing resource utilization. A study evaluating an optimal design approach (ODA) for estimating enzyme kinetic parameters used human liver microsomes and liquid chromatography-tandem mass spectrometry analysis to test 30 compounds [9]. The methodology involved:

• Multiple starting concentrations: Unlike traditional single-concentration approaches, the ODA employs multiple initial substrate concentrations to better characterize the kinetic profile across different saturation levels.

• Strategic sampling times: The design emphasizes "late time points of sampling" to improve parameter estimation, particularly for compounds with low turnover rates [9].

• Reference method comparison: The ODA was validated against the multiple depletion curves method (MDCM), a more sample-intensive approach known for reliable parameter estimation [9].

This experimental design proved effective, with CLint estimates showing >90% agreement within a 2-fold difference compared to MDCM, and Vmax and Km estimates showing >80% agreement within similar bounds [9]. The approach is particularly valuable when assessing nonlinear metabolism risks in drug development.

Protocol for Microsomal Stability Assessment

A detailed protocol for enzyme kinetic parameter determination involves:

• Reagent preparation: Compounds including traditional cytochrome P450 substrates (amodiaquine, diltiazem, imipramine, dextromethorphan, phenacetin, diclofenac) and experimental compounds dissolved in DMSO [9].

• Incubation conditions: Human liver microsomes incubated with varying substrate concentrations (typically spanning 0.1-100 μM range) in appropriate buffer systems.

• Reaction termination: At predetermined time points, reactions are stopped by addition of acetonitrile or other quenching agents.

• Analytical quantification: Sample analysis via liquid chromatography-tandem mass spectrometry (LC-MS/MS) with appropriate internal standards [9].

• Data processing: Conversion of substrate depletion data to velocity measurements, followed by kinetic modeling.

Table 4: Experimental Protocol for Modern Kinetic Analysis

Step	Procedure	Key Considerations	Typical Parameters
Substrate Preparation	Dissolve in DMSO, dilute in buffer	Final DMSO concentration ≤1% to avoid enzyme inhibition	Stock concentration: 10 mM in DMSO
Enzyme Source Preparation	Thaw microsomes, dilute in incubation buffer	Protein concentration optimization for linear kinetics	Final protein: 0.1-1 mg/mL
Incubation Setup	Mix substrate, buffer, cofactors, then initiate with enzyme	Temperature control, timing precision	Temperature: 37°C, NADPH: 1 mM
Sampling	Remove aliquots at predetermined times	Quenching method must stop reaction completely	Time points: 0, 5, 10, 20, 30, 45, 60 min
Sample Processing	Protein precipitation, centrifugation	Internal standard addition for quantification	Acetonitrile with ISTD, 1:3 ratio
Analysis	LC-MS/MS quantification	Calibration curve covering expected concentration range	MRM transitions optimized per compound
Data Transformation	Calculate depletion rates, convert to velocities	Ensure linear depletion phase for accurate rate calculation	Typically use first 3-5 time points

Contemporary Computational Approaches

The Shift to Nonlinear Regression

Current consensus in enzyme kinetics recommends against using any linear transformation method for final parameter estimation. As noted in the literature, "all linearized forms of the Michaelis-Menten equation should be avoided to calculate the kinetic parameters. Properly weighted non-linear regression methods are significantly more accurate and have become generally accessible with the universal availability of desktop computers" [35].

Nonlinear regression approaches fit the original Michaelis-Menten equation directly to untransformed data, avoiding the error distortion inherent in linear transformations. These methods provide more accurate parameter estimates with appropriate confidence intervals, especially when coupled with proper weighting schemes that account for heteroscedasticity in experimental data.

Artificial Intelligence in Kinetic Parameter Prediction

Recent advances in computational biology have introduced artificial intelligence approaches for predicting enzyme kinetic parameters. The UniKP framework, developed by researchers at the Chinese Academy of Sciences, uses pre-trained large language models to predict kcat, Km, and kcat/Km directly from protein sequences and substrate structures [41].

This approach addresses the fundamental challenge that experimental determination of kinetic parameters remains "time-consuming, expensive, and labor-intensive" [41]. The UniKP model demonstrates significant predictive power, with R² values showing up to 20 percentage point advantages over previous state-of-the-art models [41].

The framework incorporates environmental factors through EF-UniKP, a two-layer architecture that accounts for pH and temperature effects on kinetic parameters. This advancement enables more accurate predictions under physiologically relevant conditions, with R² improvements of 20% for pH considerations and 26% for temperature considerations compared to baseline models [41].

Applications in Enzyme Engineering

Computational prediction of kinetic parameters accelerates enzyme engineering and directed evolution campaigns. In a case study on tyrosine ammonia lyase (TAL), UniKP successfully identified variants with significantly improved catalytic efficiency. The RgTAL-489T variant showed a 3.5-fold higher kcat/Km value compared to wild-type enzyme [41].

This computational approach reduces the experimental burden of screening mutant libraries, enabling more efficient exploration of sequence space. By predicting kinetic parameters from sequence and structural information, these tools help prioritize variants for experimental validation, accelerating the development of enzymes for industrial and therapeutic applications.

Integrated Experimental-Computational Workflow

Diagnostic Applications and Inhibition Analysis

The Scientist's Toolkit: Essential Reagents and Materials

Table 5: Research Reagent Solutions for Enzyme Kinetics Studies

Reagent/Material	Function/Purpose	Typical Specifications	Application Notes
Enzyme Source	Biological catalyst for reaction	Purified enzyme, cell lysate, or microsomal preparation	Human liver microsomes common for drug metabolism studies [9]
Substrate	Molecule transformed by enzyme	High purity, specific for target enzyme	Multiple concentrations spanning Km for full kinetic profile
Cofactors	Enable enzymatic activity	NADPH for cytochrome P450s, ATP for kinases, etc.	Concentration optimized for saturation without inhibition
Incubation Buffer	Maintains optimal reaction conditions	Appropriate pH, ionic strength, essential ions	Typically phosphate or Tris buffers at physiological pH
Quenching Solution	Stops enzymatic reaction instantly	Acetonitrile, trichloroacetic acid, or acid/base	Must completely denature enzyme without interfering with analysis
Internal Standard	Corrects for analytical variability	Stable isotopically labeled analog of substrate/analyte	Added before sample processing for accurate quantification
Analytical Standards	Calibrates detection system	Pure samples of substrate and product	Calibration curve spanning expected concentration range
Chromatography Column	Separates analytes prior to detection	C18 reverse-phase columns common for LC-MS	Particle size 1.7-5μm for UHPLC/HPLC systems
Mass Spectrometer	Detects and quantifies analytes	Triple quadrupole with electrospray ionization	MRM mode for optimal sensitivity and selectivity
Data Analysis Software	Processes raw data, calculates kinetics	GraphPad Prism, R, Python with appropriate packages	Nonlinear regression preferred over linear transformations

Future Directions in Kinetic Parameter Estimation

The classical linear transformations—Lineweaver-Burk, Eadie-Hofstee, and Hanes-Woolf plots—represent pivotal developments in the history of enzyme kinetics, enabling generations of researchers to extract quantitative parameters from enzymatic data. Their creation transformed enzymology from a qualitative to a quantitative discipline and facilitated systematic studies of enzyme mechanisms, inhibition, and regulation [22] [35].

Within the broader thesis on Vmax and Km estimation research, these methods establish the historical foundation upon which modern approaches have been built. While contemporary best practices favor nonlinear regression for parameter estimation due to superior statistical properties, the linear transformations retain significant value for diagnostic purposes, educational applications, and preliminary data analysis [35].

The evolution of kinetic parameter estimation continues with the emergence of artificial intelligence approaches like UniKP, which can predict kinetic parameters directly from protein sequences and substrate structures [41]. These computational methods address the fundamental bottleneck of experimental kinetics—its labor-intensive nature—while potentially enabling kinetic characterization of enzymes that are difficult to study experimentally.

For today's researchers and drug development professionals, the optimal approach integrates classical understanding with modern methodology: using linear transformations for initial data assessment and visualization, nonlinear regression for robust parameter estimation, and computational prediction for screening and prioritization. This integrated strategy maximizes the strengths of each approach while minimizing their individual limitations, advancing the ultimate goal of accurate, efficient kinetic characterization in biochemical research and therapeutic development.

This technical guide examines modern nonlinear regression techniques for the accurate estimation of Michaelis-Menten kinetic parameters, Vmax and Km. We demonstrate that direct nonlinear fitting of untransformed data to the Michaelis-Menten equation provides statistically superior and more reliable parameter estimates compared to traditional linearization methods like Lineweaver-Burk plots [42] [43] [44]. This whitepaper provides researchers and drug development professionals with practical methodologies, software implementation protocols, and statistical validation frameworks for applying these techniques within enzyme kinetics and drug metabolism studies.

Within the broader thesis of understanding Vmax and Km estimation research, accurate parameter determination is fundamental. The Michaelis-Menten equation, v = (Vmax * [S]) / (Km + [S]), describes the hyperbolic relationship between initial reaction velocity (v) and substrate concentration ([S]) [12] [45]. Here, Vmax (maximum reaction velocity) defines the catalytic capacity of an enzyme system at saturation, while Km (Michaelis constant) represents the substrate concentration at half-maximal velocity and serves as an inverse measure of enzyme-substrate affinity [45]. Precise estimation of these parameters is critical for characterizing enzyme function, understanding metabolic pathways, evaluating drug mechanisms (e.g., inhibition constants, Ki), and predicting in vivo pharmacokinetics [43].

Historically, parameters were estimated using linear transformations of the Michaelis-Menten equation (e.g., Lineweaver-Burk, Eadie-Hofstee). However, these methods distort error structures, give uneven weighting to data points, and often yield biased and imprecise estimates [42] [44]. Modern computational power and sophisticated algorithms now enable direct fitting to the nonlinear model, which is statistically more rigorous and yields parameters that better reflect the true biological system.

Mathematical Foundations and the Case for Nonlinear Regression

The Michaelis-Menten Model

The model is derived from the fundamental enzyme reaction scheme: E + S ⇌ ES → E + P where E is enzyme, S is substrate, ES is the enzyme-substrate complex, and P is product. Under steady-state assumptions, this leads to the classic Michaelis-Menten equation [12] [5].

Limitations of Linear Transformation Methods

Linearization methods, while conceptually simple, violate key assumptions of linear regression:

• Error Distortion: Transformations (e.g., taking reciprocals for Lineweaver-Burk: 1/v vs. 1/[S]) dramatically alter the error distribution of the original data. Data points at low substrate concentrations, where measurement error is often highest, become disproportionately influential, skewing the fit [42] [43].
• Inaccurate Parameter Estimation: Simulation studies consistently show that linear methods produce wider confidence intervals and greater bias in estimated Vmax and Km compared to nonlinear regression [44].

Advantages of Direct Nonlinear Regression

Fitting the raw (v, [S]) data directly to the hyperbolic Michaelis-Menten model:

• Preserves the true error structure of the experimental data.
• Provides unbiased parameter estimates with statistically valid confidence intervals.
• Allows for flexible incorporation of complex error models (e.g., combined additive and proportional error) [44].
• Is directly applicable to progress curve analysis (fitting [S] or [P] vs. time data), eliminating the need for potentially inaccurate initial velocity estimates [44].

Table 1: Comparison of Traditional Linear vs. Modern Nonlinear Estimation Methods

Method	Transformation	Key Advantage	Key Disadvantage	Relative Accuracy & Precision [44]
Lineweaver-Burk	1/v vs. 1/[S]	Simple visualization	Grossly distorts errors; overweights low [S] data	Low
Eadie-Hofstee	v vs. v/[S]	Less distortion than Lineweaver-Burk	Errors are not independent; can be unreliable	Low
Direct Nonlinear (v vs. [S])	None	Correct error weighting; statistically valid	Requires computational software	High
Nonlinear (Progress Curve)	None	Uses all time-course data; no need for initial rates	Computationally more intensive	Highest

Experimental Protocols for Robust Data Generation

Accurate parameter estimation begins with high-quality kinetic data.

Protocol: Initial Velocity Assay for Direct v vs. [S] Fitting

• Reaction Conditions: Use a purified enzyme preparation at a concentration significantly lower (< 0.1 * Km) than the anticipated Km to maintain steady-state conditions. Maintain constant pH, temperature, and ionic strength.
• Substrate Range: Prepare a minimum of 8-10 substrate concentrations, spaced to adequately define the hyperbolic curve. Concentrations should bracket the Km, typically from 0.2 * Km to 5 * Km.
• Initial Rate Measurement: For each [S], initiate the reaction and measure product formation or substrate depletion over the initial linear period (typically ≤ 5% substrate conversion). Use a sensitive, continuous assay (e.g., spectrophotometric, fluorometric) where possible.
• Replicates: Perform each measurement in at least duplicate or triplicate to assess experimental variability.

Protocol: Full Time-Course (Progress Curve) Assay

This method, which provides data for the most robust nonlinear fitting [44], avoids the potential inaccuracies of estimating initial slopes.

• Reaction Initiation: In a single cuvette or well, mix enzyme and substrate to start the reaction at a known initial substrate concentration [S]₀.
• Continuous Monitoring: Record the signal corresponding to [S] or [P] at frequent time intervals until the reaction nears completion (e.g., >90% substrate depletion).
• Replication: Repeat for 5-7 different initial substrate concentrations ([S]₀), chosen as in step 3.1.
• Data Output: The final dataset is a list of time points and corresponding concentrations for each progress curve.

Computational Methods and Software Implementation

Core Algorithm: Nonlinear Least-Squares Optimization

The goal is to find the parameter values (Vmax, Km) that minimize the sum of squared residuals (SSR) between the observed data (v_obs or [S]_obs) and the model prediction [46]. SSR = Σ (y_obs_i - y_pred_i)² Algorithms like the Levenberg-Marquardt or Gauss-Newton iteratively adjust parameters to find this minimum. The process requires initial parameter guesses, which can be approximated from the raw data (e.g., Vmax from plateau velocity, Km from the [S] at Vmax/2).

Workflow for Parameter Estimation

The following diagram illustrates the integrated computational workflow for robust parameter estimation.

Implementation in Software Tools

Table 2: Essential Software Tools for Nonlinear Regression in Enzyme Kinetics

Software/Tool	Primary Use	Key Feature for Kinetics	Example Implementation
GraphPad Prism	Commercial, GUI-based analysis	Built-in Michaelis-Menten fitting with robust error estimation. Ideal for initial velocity data.	Directly input v and [S] columns, select "Nonlinear regression" > "Michaelis-Menten".
R with nls()	Open-source programming	Maximum flexibility for model definition, weighting, and error analysis.	model <- nls(v ~ (Vmax * S)/(Km + S), start=list(Vmax=100, Km=50))
Python (SciPy, lmfit)	Open-source programming	Powerful for custom scripts, batch processing, and progress curve analysis.	Use scipy.optimize.curve_fit() or the more robust lmfit.Model.
NONMEM	Specialized PK/PD modeling	Industry standard for complex nonlinear mixed-effects modeling, ideal for sparse/variable data.	Required for the rigorous fitting of progress curve data as per [44].

Critical Step: Statistical Evaluation of Fit

After optimization, always:

• Examine Residuals: Plot residuals vs. [S] or predicted v. A random scatter indicates a good fit; trends suggest model misspecification.
• Report Confidence Intervals: Use the covariance matrix from the fit to calculate the standard error and 95% confidence intervals for Vmax and Km. These are crucial for comparing parameters between experimental conditions [43].
• Use Appropriate Error Models: For progress curve data, specify the correct error structure in the model (e.g., additive, proportional, or combined) as this significantly impacts precision [44].

Case Studies & Validation from Simulation Research

A pivotal simulation study [44] compared five estimation methods using 1,000 replicates of simulated enzyme kinetic data (based on invertase kinetics: Vmax=0.76 mM/min, Km=16.7 mM) with different error models.

Table 3: Performance Comparison of Estimation Methods (Simulation Results) [44]

Estimation Method	Error Model	Median Estimated Vmax (mM/min)	Median Estimated Km (mM)	90% CI Width (Precision)
Reference (True Value)	N/A	0.760	16.70	N/A
Lineweaver-Burk (LB)	Additive	0.764	17.24	Widest
Eadie-Hofstee (EH)	Additive	0.761	16.91	Wide
Nonlinear (v vs. [S]) (NL)	Additive	0.760	16.72	Narrower
Nonlinear (Progress Curve) (NM)	Additive	0.760	16.70	Narrowest
Lineweaver-Burk (LB)	Combined*	0.781	18.95	Very Wide, Biased
Nonlinear (Progress Curve) (NM)	Combined*	0.760	16.71	Narrowest, Accurate

*Combined Error: Additive + proportional error model.

Key Findings:

• Nonlinear methods (NL and NM) were the most accurate and precise, closely recovering the true parameter values across error models.
• The progress curve nonlinear method (NM) was superior, especially under the more realistic combined error model.
• Linearization methods (LB, EH) showed significant bias and poor precision, particularly when error structures were complex. The LB plot was notably unreliable [44].
• This confirms that direct nonlinear fitting is the recommended standard for reliable Vmax and Km estimation.

The Scientist's Toolkit: Essential Research Reagent Solutions

Table 4: Key Reagents and Materials for Enzyme Kinetic Studies

Item	Function/Description	Critical for Parameter Estimation Because...
High-Purity Enzyme	Catalytic protein, recombinant or purified from tissue.	Impurities can alter observed kinetics. Concentration must be known and low relative to Km.
Characterized Substrate	Reaction substrate of known purity and concentration.	Accurate stock concentration is essential for correct [S] in the model.
Cofactors / Cations	Essential ions or molecules (e.g., Mg²⁺, NADH).	Required for full enzyme activity; omission lowers apparent Vmax.
Assay Buffer System	Maintains constant pH and ionic strength (e.g., Tris, phosphate).	Prevents pH-induced changes in enzyme activity during the assay.
Stopping Agent / Detection System	Halts reaction (acid) or monitors product (chromogen, fluorescent probe).	Enables accurate measurement of initial velocity or continuous progress.
Microplate Reader / Spectrophotometer	Instrument for high-throughput or precise absorbance/fluorescence measurement.	Allows collection of high-quality, reproducible data points for robust fitting.
Statistical Software	Tools like GraphPad Prism, R, Python as listed in Table 2.	Enables the application of the recommended nonlinear regression techniques.

Advanced Applications: Beyond Basic Michaelis-Menten

The principles of direct nonlinear fitting extend to more complex kinetic scenarios crucial in drug development:

• Inhibition Kinetics: Directly fit data to equations for competitive, non-competitive, or uncompetitive inhibition to estimate Ki.
• Multi-Substrate Kinetics: Fit data to models for ping-pong or sequential mechanisms.
• Allosteric Enzymes: Use the Hill equation to estimate Vmax, K0.5, and the Hill coefficient.
• In vivo Pharmacokinetics: Apply nonlinear mixed-effects modeling (NONMEM) to estimate metabolic clearance Vmax and Km from population pharmacokinetic data.

Within the ongoing research thesis on Vmax and Km estimation, the adoption of modern nonlinear regression represents a critical methodological advancement. Moving away from historically convenient but flawed linear transformations to direct curve fitting of untransformed data using powerful software tools ensures that parameter estimates are statistically valid, accurate, and precise. This guide provides the experimental and computational framework for researchers to implement these robust methods, thereby enhancing the reliability of kinetic data that underpins mechanistic biochemistry, enzymology, and quantitative drug development.

Accurately predicting how a drug candidate will be metabolized and cleared from the body is a cornerstone of modern pharmacokinetics and a critical determinant of its success in development. At the heart of this prediction lies the concept of metabolic intrinsic clearance (CLint), a fundamental measure of the liver's inherent ability to remove a drug via enzymatic metabolism in the absence of limitations from blood flow or binding [47]. For drugs metabolized by enzymes that follow Michaelis-Menten kinetics, CLint is rigorously defined as the ratio of the two primary enzyme kinetic parameters: the maximum reaction velocity (Vmax) and the Michaelis constant (Km) [48]. This relationship, CLint = Vmax / Km, provides a crucial bridge between in vitro experimental data and the prediction of in vivo pharmacokinetic behavior.

The broader thesis of Vmax and Km estimation research is centered on refining the accuracy, efficiency, and translational power of these measurements. Traditional methods, while foundational, often rely on initial rate measurements of metabolite formation, which can be labor-intensive and may not fully capture the kinetics of substrate depletion over time [49]. Recent research, therefore, focuses on robust, integrated approaches that account for complex real-world scenarios such as non-specific binding, enzyme instability during incubation, and the need to translate findings from laboratory systems to human physiological outcomes [47] [48]. This guide details the core methodologies, from foundational equations to advanced experimental protocols, that enable researchers to reliably estimate CLint from Vmax and Km, thereby de-risking drug development and optimizing therapeutic efficacy and safety [50].

Core Kinetic Equations and Definitions

The estimation of CLint is built upon a framework of equations derived from the Michaelis-Menten model. The following table summarizes the key equations and their specific applications in pharmacokinetics.

Table 1: Key Michaelis-Menten Equations for Enzyme Kinetics and Clearance Estimation

Equation Name/Description	Mathematical Form	Key Variables & Applications
Classic Michaelis-Menten [47] [50]	( V0 = \frac{V{max} \times C}{K_m + C} )	Determines initial reaction velocity ((V_0)). Used to model enzyme saturation.
Intrinsic Clearance (CLint) [48]	( CL{int} = \frac{V{max}}{K_m} )	Defines the inherent metabolic capacity. Foundational for in vitro to in vivo scaling.
Clearance as a Function of Concentration [47] [50]	( Cl = \frac{V{max} \times C}{Km + C} )	Models how total clearance (Cl) changes with substrate concentration (C).
Dose Rate at Steady State [47] [50]	( DR = \frac{V{max} \times C{ss}}{Km + C{ss}} )	Calculates the infusion or dosing rate (DR) required to maintain a target steady-state plasma concentration ((C_{ss})). Critical for drugs with nonlinear kinetics.
Enzyme Saturation Percentage [47] [50]	( Percent\ Saturation (\%) = \frac{100 \times C}{K_m + C} )	Estimates the fraction of enzyme active sites occupied by substrate at a given concentration (C). Vital for assessing the potential for nonlinear, concentration-dependent pharmacokinetics.

Methodologies for Estimating Vmax, Km, and CLint

Several established experimental methods are used to determine Vmax and Km, from which CLint is calculated. The choice of method depends on the specific research question, the properties of the compound, and the desired balance between throughput and accuracy.

The Multiple Depletion Curves Method (MDCM)

The Multiple Depletion Curves Method (MDCM) is a robust approach that analyzes the substrate depletion profile over time at multiple starting concentrations [49] [51]. Instead of measuring metabolite formation, it directly monitors the disappearance of the parent compound. A set of depletion curves is simultaneously fitted to an integrated form of the Michaelis-Menten equation to solve for Vmax and Km. This method is particularly advantageous for compounds where metabolite standards are unavailable or for pathways with multiple metabolites [49]. Studies have validated MDCM against traditional methods, showing good overall agreement and demonstrating its robustness in coping with different substrate turnover rates through Monte Carlo simulations [49] [51].

Experimental Protocol for MDCM [49]:

• Incubation Setup: Prepare a series of incubations (e.g., in human liver microsomes or hepatocytes) with the test compound at 5-8 different starting concentrations, typically spanning a range from well below to above the anticipated Km.
• Time Course Sampling: For each starting concentration, aliquot samples from the incubation mixture at 6-8 pre-determined time points (e.g., 0, 5, 15, 30, 45, 60 minutes).
• Reaction Termination: Immediately terminate the metabolic reaction in each sample, usually by adding an equal volume of an organic solvent like acetonitrile.
• Sample Analysis: Quantify the remaining concentration of the parent compound in each sample using a sensitive analytical method (e.g., LC-MS/MS).
• Data Analysis: Pool all concentration-time data from all starting concentrations. Use nonlinear regression software to fit the data to the substrate depletion model, solving for a single, shared set of Vmax and Km values that best describe the entire dataset.
• CLint Calculation: Calculate CLint as the ratio of the fitted parameters: ( CL{int} = V{max} / K_m ).

The Initial Formation Rate of Metabolite Method (IFRMM)

The Initial Formation Rate of Metabolite Method (IFRMM) is the classical and most direct approach [49]. It involves measuring the initial velocity (V₀) of metabolite formation at several substrate concentrations under conditions where less than 10-15% of the substrate is consumed, ensuring the reaction rate is constant.

Experimental Protocol for IFRMM [47] [48]:

• Incubation Setup: Set up separate incubations for each substrate concentration. The concentration range should bracket the expected Km (e.g., 0.2Km to 5Km).
• Short Incubation: Incubate for a short, linear time period (typically 2-10 minutes) where product formation is directly proportional to time.
• Reaction Termination and Analysis: Stop the reaction and measure the concentration of the specific metabolite formed using analytical techniques like HPLC or LC-MS/MS.
• Curve Fitting: Plot the initial velocity (V₀) against substrate concentration ([S]). Fit the data using nonlinear regression to the classic Michaelis-Menten equation to estimate Vmax and Km.
• CLint Calculation: Compute ( CL{int} = V{max} / K_m ).

The In Vitro T½ Method

The In Vitro T½ Method is a simpler, substrate depletion-based approach used for high-throughput screening. It assumes first-order kinetics (where [S] << Km) and estimates CLint from the observed half-life of the substrate in the incubation system [49].

Experimental Protocol for the T½ Method [49]:

• Low-Concentration Incubation: Incubate the test compound at a single, low concentration (ideally << Km).
• Time Course Sampling: Take samples over time as the substrate depletes.
• Half-life Determination: Plot the natural logarithm of substrate concentration versus time. The slope of the linear phase is the elimination rate constant (k), from which the in vitro half-life is calculated: ( t_{1/2} = \frac{ln(2)}{k} ).
• CLint Calculation: Intrinsic clearance is then calculated using the formula: ( CL{int} = \frac{ln(2)}{t{1/2}} \times \frac{\text{Incubation Volume}}{\text{Microsomal Protein or Cell Number}} ).

Table 2: Comparison of Key Methods for Estimating Enzyme Kinetic Parameters

Feature	Multiple Depletion Curves (MDCM)	Initial Formation Rate (IFRMM)	In Vitro T½ Method
Primary Measurement	Depletion of parent compound over time [49].	Formation of metabolite at initial rates [49].	Depletion of parent compound at a single low concentration [49].
Key Assumption	Integrated Michaelis-Menten kinetics applies; enzyme activity is stable [49].	Initial rate conditions (minimal substrate turnover) [47].	Substrate concentration is much lower than Km (first-order kinetics) [49].
Throughput	Moderate.	Low (requires many incubations and metabolite standard).	High.
Best Application	Compounds with unknown or multiple metabolites; robust parameter estimation [49].	Definitive characterization of a specific metabolic pathway [48].	Early-stage screening and ranking of compound CLint [49].
Limitations	Complex data analysis; sensitive to enzyme activity loss during incubation [49].	Labor-intensive; requires synthetic metabolite standards.	Inaccurate for compounds where the low-concentration assumption is violated [49].

From In Vitro Data to In Vivo Prediction

Translating in vitro estimates of Vmax and Km into a prediction of human hepatic clearance is a critical step that requires careful scaling and consideration of physiological factors.

Scaling and Correction Factors

The first step is to scale the microsomal or hepatocyte-based CLint to values representing the whole liver [48]. This involves using scaling factors:

• Microsomal Protein per Gram of Liver (MPPGL): Typically ~40-50 mg microsomal protein per gram liver.
• Human Liver Weight: Average ~20 g liver per kg body weight, or ~1500 g total liver weight for a 70 kg adult. The scaled hepatic intrinsic clearance (CLint,h) is calculated as: ( CL{int,h} = CL{int} \times MPPGL \times Liver\ Weight ).

A key challenge is non-specific binding of the drug to incubation components (e.g., microsomal lipids). The unbound fraction in the incubation ((f{u,inc})) must be measured and used to calculate the unbound intrinsic clearance (CLint,u): ( CL{int,u} = \frac{CL{int}}{f{u,inc}} ). Studies have shown that failing to correct for this binding can lead to significant underprediction of in vivo clearance, particularly for highly bound drugs [48].

Integrating Clearance into Pharmacokinetic Models

The final scaled and corrected CLint,u is incorporated into liver models to predict in vivo hepatic clearance (CLh). The most common models are:

• Well-Stirred Model: ( CLh = \frac{Qh \times fu \times CL{int,u}}{Qh + fu \times CL{int,u}} ) Where (Qh) is hepatic blood flow and (f_u) is the unbound fraction in blood.
• Parallel Tube and Dispersion Models: More complex models that may offer improved predictions for certain compounds.

For drugs exhibiting Michaelis-Menten kinetics in vivo (where plasma concentrations approach or exceed Km), the steady-state concentration ((C{ss})) is related to the dosing rate (DR) by the equation: ( DR = \frac{V{max} \times C{ss}}{Km + C_{ss}} ) [47] [50]. This nonlinear relationship is critical for dose adjustment and managing drugs with a narrow therapeutic window.

Experimental Protocols in Detail

Successful estimation of reliable kinetic parameters depends on meticulous execution of standardized protocols. This section details the setup for a robust microsomal incubation study.

Key Materials and Reagent Preparation

• Test Compound Stock Solution: Prepare a high-concentration stock (e.g., 10 mM) in a suitable solvent (DMSO, acetonitrile). Final solvent concentration in incubation should not exceed 1% (v/v) to avoid enzyme inhibition.
• Co-factor Solution: Prepare a Nicotinamide Adenine Dinucleotide Phosphate (NADPH) regenerating system or a solution of pre-formed NADPH to initiate the reaction. This is essential for cytochrome P450 activity.
• Potassium Phosphate Buffer (100 mM, pH 7.4): The standard buffer for maintaining physiological pH.
• Human Liver Microsomes (HLM) or Hepatocytes: Commercially available pooled HLMs are standard. Thaw on ice and keep cold until use.
• Quenching Solution: Typically ice-cold acetonitrile or methanol containing an internal standard for analysis.

Incubation and Sampling Procedure

• Pre-incubation: In a temperature-controlled water bath or incubator block (37°C), combine buffer, microsomal protein (e.g., 0.1-0.5 mg/mL), and the test compound at the desired starting concentration. Use a range of concentrations (e.g., 0.1, 0.3, 1, 3, 10, 30 µM).
• Reaction Initiation: Pre-equilibrate the mixture for 2-3 minutes. Start the metabolic reaction by adding the NADPH co-factor solution. For "time zero" controls, add quenching solution before adding NADPH.
• Time Course Sampling: At predetermined times (e.g., 0, 5, 15, 30, 45, 60 min), remove an aliquot (e.g., 50 µL) from the incubation mixture and immediately transfer it to a tube containing a large volume of quenching solution (e.g., 150 µL acetonitrile) to stop the reaction.
• Sample Processing: Vortex, then centrifuge (e.g., 4000 x g, 10 min) to precipitate proteins. Transfer the supernatant for analysis by LC-MS/MS.

Critical Analytical Considerations

• Analytical Method: LC-MS/MS is the gold standard for sensitivity and specificity. The method must be validated for the parent compound.
• Calibration Standards & QC Samples: Prepare fresh calibration curves and quality control samples in a matrix matching the quenched incubation samples.
• Nonspecific Binding Assessment: Determine the fraction unbound ((f_{u,inc})) in the incubation matrix using methods like equilibrium dialysis or ultracentrifugation [48].

The Scientist's Toolkit

Table 3: Essential Research Reagents and Materials for CLint Studies

Category	Item/Solution	Primary Function in Experiment
Biological System	Pooled Human Liver Microsomes (HLM) or Cryopreserved Human Hepatocytes	Provides the metabolically active enzymes (CYPs, UGTs, etc.) in a physiologically relevant system. The source of Vmax and Km [49] [48].
Co-factors	NADPH Regenerating System (Glucose-6-Phosphate, G6PD, NADP+) or pre-formed NADPH	Supplies the reducing equivalents required for oxidative metabolism by cytochrome P450 enzymes, initiating the reaction [49].
Buffer System	Potassium Phosphate Buffer (pH 7.4)	Maintains the physiological pH necessary for optimal enzyme activity and stability during incubation [49].
Analytical Tools	LC-MS/MS System with Validated Bioanalytical Method	Enables highly sensitive and specific quantification of the parent compound (for depletion methods) or metabolite (for formation methods) in complex biological matrices [49].
Substrates (Examples)	CYP-selective probe substrates (e.g., Diclofenac for CYP2C9, Dextromethorphan for CYP2D6) [49]	Used for method validation, determining enzyme activity of specific pathways, and as positive controls.
Binding Assessment	Equilibrium Dialysis or Ultracentrifugation Apparatus	Measures the unbound fraction of drug in the incubation ((f_{u,inc})), which is critical for correcting CLint and achieving accurate in vivo predictions [48].

Applications in Drug Development: Enzyme Induction and Inhibition

Accurate Vmax and Km data transcends basic clearance prediction; it is fundamental for assessing drug-drug interaction (DDI) risks via enzyme modulation [47] [50].

• Identifying Enzyme Inhibitors: A test compound that decreases the Vmax (or increases the apparent Km) of a probe substrate for a specific enzyme (e.g., CYP3A4) is a potential inhibitor. The inhibition constant ((K_i)) can be derived from these changes, which is used to predict the magnitude of clinical DDI.
• Identifying Enzyme Inducers: Chronic exposure to a drug can increase the amount of enzyme present, effectively increasing the Vmax for its own metabolism or that of co-administered drugs. In vitro induction studies (e.g., in human hepatocytes) assess changes in mRNA or activity of enzymes like CYP3A4 over several days.
• Quantifying In Vivo Impact: The in vivo inhibitory potential can be estimated as the ratio of the maximum plasma concentration of the inhibitor ((C{max})) to its inhibition constant ((Ki)) [47] [50]. This ratio helps stratify DDI risk and guide clinical study design.

Optimizing Accuracy: Troubleshooting Common Issues in Kinetic Parameter Estimation

The accurate determination of Michaelis-Menten kinetic parameters, Vmax (maximum reaction velocity) and Km (Michaelis constant), forms the cornerstone of quantitative enzymology with profound implications across biochemical research, drug discovery, and diagnostic medicine [52]. Vmax represents the theoretical maximum rate of an enzyme-catalyzed reaction under saturating substrate conditions, while Km indicates the substrate concentration at half Vmax and serves as an inverse measure of enzyme-substrate affinity [52] [53]. Errors in estimating these parameters directly compromise fundamental research, the development of enzyme-targeted therapeutics, and the accuracy of clinical diagnostics [52] [54]. This guide addresses three pervasive sources of experimental error—substrate depletion, enzyme impurity, and inhibition effects—that systematically distort kinetic measurements. We frame these technical challenges within the broader thesis that robust Vmax and Km estimation requires not only meticulous experimental execution but also an understanding of the underlying assumptions and limitations of classical kinetic models [15].

Understanding and Diagnosing Experimental Errors

Substrate Depletion and Non-Linear Progress Curves

A fundamental assumption of the Michaelis-Menten equation and initial velocity measurements is that substrate concentration remains essentially constant, requiring that less than 10% of the substrate is consumed during the assay period [54]. Substrate depletion violates this assumption, leading to non-linear progress curves and significant underestimation of enzyme activity [52].

• Mechanism of Error: In a typical assay, the reaction progress follows three phases: an initial lag, a linear phase (where velocity is measured), and a final plateau as substrate is exhausted [52]. When enzyme concentration is excessively high relative to substrate, the linear phase vanishes; substrates are consumed entirely during the lag phase before instrumental recording effectively begins. The instrument then records a flat, non-productive trace, which is falsely interpreted as very low or null enzyme activity [52].
• Clinical Case Example: A paradigmatic case involved a serum creatine kinase (CK) assay. An autoanalyzer reported a result of 12 U/L, which conflicted with the patient's clinical picture. Investigation revealed the instrument had flagged an error ("E") due to an abnormal progress curve, but a new technician reported the subsequent (still erroneous) value. Upon a 1:100 sample dilution, the corrected CK activity was 150,892 U/L—a discrepancy of four orders of magnitude caused by substrate (creatine phosphate) exhaustion [52].
• Diagnosis: The primary diagnostic tool is continuous monitoring of the reaction progress curve (absorbance vs. time). A healthy kinetic assay shows a prolonged linear phase. A curve that plateaus rapidly or shows a brief linear segment that quickly bends to a plateau is indicative of substrate depletion [52]. This phenomenon is analogous to the "prozone effect" in immunoassays and has been documented for numerous high-abundance analytes [52].

The Impact of Enzyme Purity on Assay Specificity and Reproducibility

Enzyme purity is a non-negotiable requirement for reliable kinetics. Impurities act as confounding variables that alter observed reaction rates, leading to incorrect Vmax and Km values [55] [56].

• Sources and Consequences of Impurity:

  • Contaminating Enzymatic Activities: Residual host cell proteins, including other enzymes, can catalyze side reactions, consume substrate, or generate product, leading to inflated velocity measurements [55].
  • Chemical Inhibitors or Activators: Carryover of cellular components like endotoxins can non-specifically inhibit or stabilize the enzyme of interest [55].
  • Macromolecular Contaminants: Residual host DNA can interfere with detection systems, particularly in modern luminescent or PCR-coupled assays, causing false signals [55].
  • Altered Physical State: Protein aggregates or degraded enzyme fragments can show different kinetic properties or no activity, effectively reducing the concentration of functional enzyme [55].

• Quality Disparity: The impurity profile of a diagnostic-grade enzyme is markedly different from an industrial-grade preparation. Analysis via SDS-PAGE and HPLC-Size Exclusion Chromatography (SEC) reveals a diagnostic-grade enzyme as a single, sharp band/peak, whereas industrial-grade samples show multiple bands and heterogeneous peaks indicating contaminants and aggregates [55].

Inhibition Effects: Mechanisms and Misinterpretation

Inhibition is a primary mechanism of drug action but can also be an unintended source of error from buffer components, cofactor chelators, or product accumulation. Different inhibition mechanisms uniquely distort the relationship between velocity and substrate concentration [57] [53].

• Competitive Inhibition: The inhibitor (I) competes with the substrate (S) for the active site. This increases the apparent Km (requiring more substrate to reach half-saturation) but does not affect Vmax, as sufficient substrate can outcompete the inhibitor [57] [53]. A classic pharmaceutical example is methotrexate, a competitive inhibitor of dihydrofolate reductase [57].
• Non-Competitive Inhibition: The inhibitor binds an allosteric site, distinct from the active site, on both the free enzyme and the enzyme-substrate complex. This binding reduces the enzyme's catalytic efficiency or total functional concentration, thereby decreasing Vmax. The affinity for substrate is unchanged, so Km remains unaffected [57] [53].
• Uncompetitive Inhibition: The inhibitor binds only to the enzyme-substrate complex, "locking" it in a state. This paradoxically increases apparent affinity (lowers apparent Km) because substrate binding facilitates inhibitor binding. It also decreases Vmax [53].
• Mixed Inhibition: The inhibitor binds to both the free enzyme and the enzyme-substrate complex but with different affinities. This always decreases Vmax and can either increase or decrease the apparent Km, depending on which state (E or ES) the inhibitor prefers [53].

Misidentifying the type of inhibition, or failing to account for it, leads to profound errors in characterizing an enzyme's intrinsic kinetics or a drug's mechanism of action.

Table 1: Summary of Common Experimental Errors, Their Effects on Kinetic Parameters, and Diagnostic Solutions

Error Type	Primary Effect on Assay	Impact on Vmax	Impact on Km	Key Diagnostic Methods
Substrate Depletion [52]	Non-linear progress curve; falsely low activity reading	Severe underestimation	Overestimation	Visual inspection of progress curve; automatic analyzer error flags; sample dilution test.
Enzyme Impurity [55] [56]	Loss of specificity; altered reaction rate; assay instability	Variable (often overestimation)	Variable	HPLC-SEC (aggregates); LC-MS/MS (host cell proteins); LAL assay (endotoxins); SDS-PAGE.
Competitive Inhibition [57] [53]	Substrate outcompetes inhibitor at high [S]	Unchanged	Increased	Lineweaver-Burk plot: lines intersect on y-axis. Vmax is restored with high [S].
Non-Competitive Inhibition [57] [53]	Inhibitor binds regardless of substrate presence	Decreased	Unchanged	Lineweaver-Burk plot: lines intersect on x-axis.
Uncompetitive Inhibition [53]	Inhibitor binds only to ES complex	Decreased	Decreased	Lineweaver-Burk plot: parallel lines.

Workflow for Identifying and Correcting Kinetic Assay Errors

Detailed Experimental Protocols for Error Identification and Correction

Protocol for Detecting and Correcting Substrate Depletion

This protocol is adapted from clinical laboratory practice and high-throughput screening (HTS) assay development [52] [54].

• Initial Assay Setup: Perform the kinetic assay under standard conditions.
• Progress Curve Analysis: Do not rely on a single endpoint or a few time points. Continuously monitor the signal (e.g., absorbance at 340 nm for NADPH) over the entire reaction time. Visually inspect the plot for linearity [52].
• Dilution Test: If the progress curve shows an abnormally short linear phase or an early plateau, serially dilute the enzyme sample (e.g., 1:10, 1:100, 1:1000) and repeat the assay [52].
• Validation: The corrected enzyme activity is calculated as: Observed Activity × Dilution Factor. True activity is confirmed when the progress curve from the diluted sample exhibits a prolonged linear phase (>5 minutes or suitable for the assay) [52] [54].
• Automation: For HTS, implement software flags to automatically re-run samples showing progress curve anomalies at a higher dilution [52].

Protocol for Validating Enzyme Purity

A multi-technique approach is required to fully characterize an enzyme preparation [55] [56].

• Identity and Mass Purity:
  • SDS-PAGE and Native-PAGE: Confirm a single band at the expected molecular weight under denaturing (SDS) and native conditions. Any additional bands indicate contaminating proteins [55].
  • HPLC-Size Exclusion Chromatography (SEC): Quantify the percentage of the target enzyme in its correct oligomeric state. A single, symmetrical peak should constitute >95% of the total protein. Leading or trailing shoulders indicate aggregates or fragments [55].
• Specific Activity Validation:
  • Measure enzyme activity under standardized conditions (pH, temperature, saturating [S]).
  • Determine protein concentration via a specific method (e.g., A280 with extinction coefficient).
  • Calculate specific activity (units/mg protein). Compare this value between batches; a decrease may indicate loss of purity or activity [54] [56].
• Analysis of Specific Impurities:
  • Host Cell Proteins (HCPs): Use LC-MS/MS or ELISA to detect and quantify residual proteins from the expression system down to ppm levels [55].
  • Nucleic Acids: Use qPCR to quantify residual host DNA to ensure it meets regulatory thresholds (<10 ng/mg) [55].
  • Endotoxins: Perform the Limulus Amebocyte Lysate (LAL) assay to ensure endotoxin levels are <0.1 EU/mg for diagnostic applications [55].

Protocol for Characterizing Inhibition Type

This protocol uses the substrate depletion method, which is robust for compounds with low turnover, and standard initial velocity analyses [58] [9].

• Substrate Depletion Assay (for Metabolic Enzymes like CYP450) [58] [9]:
  • Incubation: Incubate the enzyme (e.g., liver microsomes) with varying starting concentrations of substrate (e.g., 0.5x, 1x, 2x, 5x, and 10x of the estimated Km) in the presence and absence of a fixed concentration of inhibitor.
  • Sampling: Take multiple time points (e.g., 0, 5, 15, 30, 45, 60 min) to track substrate loss.
  • Analysis: Fit the substrate depletion curves to an appropriate model (e.g., monoexponential decay for single-enzyme systems) to obtain the half-life (t₁/₂) and intrinsic clearance (CLint) for each condition.
  • Parameter Estimation: Use non-linear regression to fit the velocity (calculated from CLint) vs. substrate concentration data to the Michaelis-Menten equation, yielding apparent Vmax and Km values in the presence of the inhibitor. Compare these to control values.
• Initial Velocity Analysis with Varied [S] and [I]:
  • Perform initial velocity assays at multiple substrate concentrations (spanning 0.2–5.0 × Km) in the presence of at least three different inhibitor concentrations (including zero) [54].
  • Plot the data on a Lineweaver-Burk plot (1/v vs. 1/[S]).
  • Interpretation:
    • Competitive: Lines intersect on the y-axis (1/Vmax unchanged).
    • Non-Competitive: Lines intersect on the x-axis (Km unchanged).
    • Uncompetitive: Parallel lines.
    • Mixed: Lines intersect in the second quadrant [57] [53].

Mechanisms of Reversible Enzyme Inhibition

Advanced Methodologies and Optimized Experimental Design

Moving beyond basic error correction, robust kinetic research requires advanced methodologies that account for model limitations and employ optimal experimental design [15] [9].

• Addressing Model Limitations with the Total Quasi-Steady-State Approximation (tQSSA): The classical Michaelis-Menten equation, derived using the standard quasi-steady-state approximation (sQSSA), is valid only when the total enzyme concentration ([E]ₜ) is much lower than the sum of Km and substrate concentration ([S]ₜ) [15]. This condition is frequently violated in vivo and can be in in vitro systems with high enzyme concentrations. Using the sQSSA model under these conditions leads to biased estimates of Vmax and Km. The tQSSA model, while mathematically more complex, provides accurate kinetic parameter estimation across all concentration ranges, including when [E]ₜ is similar to or greater than [S]ₜ or Km [15]. Bayesian inference approaches based on the tQSSA model can yield unbiased estimates from progress curve data without restrictive concentration requirements [15].

• Optimal Experimental Design (ODA) for Substrate Depletion Assays: Traditional single-starting-concentration depletion assays can be suboptimal for parameter estimation. An ODA using multiple starting substrate concentrations (C₀) and sampling to late time points has been experimentally validated to provide reliable estimates of Vmax, Km, and intrinsic clearance (CLint) [9]. This design is particularly effective for assessing the risk of non-linear (saturable) metabolism in drug discovery. For a set of 30 compounds, this ODA produced estimates of CLint, Vmax, and Km that were within a 2-fold difference of those from a more resource-intensive reference method in >90% and >80% of cases, respectively [9].

• Design of Experiments (DoE) for Assay Optimization: Instead of the traditional "one-factor-at-a-time" (OFAT) approach, which can take over 12 weeks, a fractional factorial DoE approach can identify key factors affecting enzyme activity and optimize assay conditions in less than 3 days [59]. This method systematically varies multiple factors simultaneously (e.g., buffer pH, ionic strength, cofactor concentration, [enzyme], [substrate]), allowing for the efficient modeling of interactions between variables and the identification of optimal conditions with minimal experimental runs [59].

The Scientist's Toolkit: Essential Reagents and Materials

Table 2: Key Research Reagent Solutions for Robust Kinetic Assays

Item	Function & Rationale	Key Considerations & Reference
N-Acetyl Cysteine (NAC)	Reducing agent used to reactivate sulfhydryl groups in enzyme active sites (e.g., creatine kinase) prone to oxidation, preserving catalytic activity [52].	Concentration must be optimized; included in many commercial clinical assay reagents [52].
Adenosine Monophosphate (AMP) & Diadenosine Pentaphosphate	Inhibitors of contaminating adenylate kinase (AK) activity. AK, released from platelets or cells, can consume ATP/ADP and interfere with coupled assays, leading to overestimation of target enzyme activity [52].	Essential for assays in complex biological matrices like serum [52].
Diagnostic-Grade Enzymes	Enzymes (e.g., Glucose-6-Phosphate Dehydrogenase in coupled assays) purified and validated to meet stringent impurity thresholds for diagnostic use [55].	Superior to research-grade: characterized by HPLC-SEC (single peak), LC-MS/MS (low HCP), qPCR (low DNA), LAL (<0.1 EU/mg) [55].
Reference Inhibitors	Well-characterized inhibitors with known mechanism (competitive, non-competitive) and potency (IC₅₀, Kᵢ) for the target enzyme.	Used as positive controls to validate assay performance and inhibition screening protocols [54].
Stable Isotope-Labeled Substrates/Products	Internal standards for mass spectrometry-based depletion or metabolite formation assays. Enable precise quantification by correcting for ionization efficiency and matrix effects [58] [9].	Critical for accurate LC-MS/MS analysis in metabolic stability and CYP450 kinetic studies [9].

Accurate estimation of the kinetic parameters Vmax (maximum reaction velocity) and Km (Michaelis constant) is a cornerstone of enzymology research with direct implications for understanding metabolic pathways, characterizing enzyme mechanisms, and facilitating drug discovery [54] [60]. These parameters are not merely descriptive numbers; they are fundamental to a quantitative understanding of how enzymes behave in vitro, which in turn informs predictions of their function in vivo and their suitability as therapeutic targets. Vmax provides insight into the catalytic capacity of an enzyme, while Km quantifies its affinity for a substrate [60]. However, reliable estimation of these parameters is entirely contingent upon meticulously optimized assay conditions. Missteps in defining enzyme and substrate concentrations, or in failing to establish initial velocity conditions, lead to systematic errors, unreliable data, and flawed scientific conclusions [54] [61].

This guide is framed within the broader thesis that robust biochemical research hinges on rigorous assay design. The process of optimizing enzyme and substrate concentrations is the critical bridge between a conceptual kinetic model and high-quality, reproducible data. As demonstrated in pharmacokinetics for monoclonal antibodies, poor study design—such as using a limited range of substrate (dose) concentrations—can result in widely divergent and unreliable estimates for Vmax and Km, undermining the entire modeling effort [62]. Therefore, the protocols and guidelines detailed herein are not just procedural steps but essential practices for generating data that accurately reflects enzyme behavior and supports valid scientific inference.

Foundational Principles: Michaelis-Menten Kinetics and Initial Velocity

The relationship between substrate concentration ([S]) and the initial reaction velocity (v₀) for many single-substrate enzymes is described by the Michaelis-Menten equation [54] [60]:

v₀ = (Vmax [S]) / (Km + [S])

Where:

• Vmax is the maximum theoretical velocity when the enzyme is fully saturated with substrate.
• Km is the substrate concentration at which the reaction velocity is half of Vmax.
• kcat (the turnover number) can be derived as Vmax / [E]total, representing the number of substrate molecules converted to product per enzyme molecule per unit time [63] [60].

The accurate determination of these parameters rests on the principle of initial velocity. This refers to the very early, linear phase of the reaction where less than 10% of the substrate has been converted to product [54]. During this phase, several complicating factors are minimized: substrate depletion is negligible, product inhibition is insignificant, and the enzyme remains stable [54]. Measuring outside this linear range invalidates the assumptions of the Michaelis-Menten model, leading to incorrect parameter estimates.

Table 1: Consequences of Not Operating Under Initial Velocity Conditions [54]

Factor	Consequence for Assay and Data
Substrate Depletion	Reaction rate decreases over time, violating steady-state assumption.
Product Inhibition	Accumulating product inhibits the enzyme, causing non-linear progress curves.
Enzyme Instability	Loss of active enzyme over time leads to an underestimation of true activity.
Invalid Kinetic Analysis	The derived Km and Vmax values are artefactual and unreliable.

Establishing the linear phase requires an experiment where product formation is monitored over time at several enzyme concentrations. The appropriate enzyme concentration is one that yields a linear progress curve for a sufficient duration to allow reliable measurement [54] [64].

A Systematic Pipeline for Enzyme Characterization and Assay Development

A robust approach to assay optimization follows a logical, stepwise pipeline. The following workflow integrates best practices from foundational guides and applied research protocols [63] [54].

Enzyme Characterization and Kinetic Analysis Workflow

Experimental Protocol: Defining the Linear Phase and Enzyme Concentration

Objective: To identify the time window during which product formation is linear with time and the range of enzyme concentrations where the initial velocity (v₀) is directly proportional to enzyme concentration [E] [63] [54].

Materials:

• Purified enzyme.
• Substrate stock solution.
• Assay buffer (optimal pH and ionic strength).
• Necessary cofactors.
• Equipment for reaction initiation, quenching, and signal detection (e.g., plate reader, fluorimeter).

Method:

• Prepare a master reaction mix containing buffer, cofactors, and substrate at a concentration near or below its anticipated Km [54].
• Serially dilute the enzyme stock to create a range of concentrations (e.g., spanning an order of magnitude) [64].
• Initiate reactions by adding enzyme to the master mix. For each enzyme concentration, perform the reaction in triplicate.
• At multiple, closely spaced time intervals (e.g., 0, 1, 2, 3, 5, 7, 10, 15 minutes), quench the reaction or directly measure the signal if using a continuous method.
• Plot product formed (or signal) versus time for each enzyme concentration.

Analysis & Decision Criteria:

• Linear Time Window: For each progress curve, identify the early time period where the increase in product is linear (R² > 0.98). The shortest common linear time window across all enzyme dilutions should be used for subsequent initial velocity measurements [54].
• Linear [E] Range: Plot the initial velocity (slope of the linear phase) against the enzyme concentration. The range where this relationship is linear (v₀ ∝ [E]) defines the acceptable enzyme concentrations for the assay. An enzyme concentration in the middle of this linear range is typically chosen for the formal kinetic assay [63].

Experimental Protocol: Michaelis-Menten Kinetics for Km and Vmax

Objective: To determine the kinetic parameters Km and Vmax by measuring initial velocities across a wide range of substrate concentrations and fitting the data to the Michaelis-Menten equation [63] [60].

Materials: As above, with a focus on preparing a comprehensive substrate concentration series.

Method:

• Based on prior knowledge or literature, choose a substrate concentration range that spans from well below to well above the expected Km. A recommended series is 0.2, 0.5, 1, 2, 5, 10, and 15 times the estimated Km [63] [54]. Use at least 8 different concentrations.
• Using the optimal enzyme concentration and linear time window determined in Section 3.1, run initial velocity assays in triplicate for each substrate concentration [S].
• Include essential controls: no-enzyme blanks (for background signal) and, if possible, a positive control with a known enzyme or substrate standard.

Analysis:

• Correct the measured velocities by subtracting the background signal from the no-enzyme control.
• Plot v₀ versus [S]. Fit the data using non-linear regression to the Michaelis-Menten equation. Avoid linear transformations like Lineweaver-Burk plots, as they distort error distribution [63].
• From the fit, extract Vmax and Km with their respective 95% confidence intervals.
• Calculate the derived parameters:
  • kcat = Vmax / [E]total (where [E]total is the molar concentration of active enzyme).
  • Catalytic efficiency = kcat / Km.

Table 2: Guidelines for Substrate Concentration Range and Data Fitting [63] [54] [61]

Aspect	Recommended Guideline	Rationale and Consequence
Substrate Range	Span 0.2–5.0 x Km. Include points both below and above Km.	Concentrations below Km inform on enzyme affinity; concentrations above Km are needed to approach Vmax and define the plateau.
Point Density	Use minimum of 8 substrate concentrations. More points improve fit reliability.	Sparse data can lead to high uncertainty in fitted parameters, especially if they cluster in one region (e.g., only below Km).
Fitting Method	Non-linear regression (e.g., in GraphPad Prism).	Provides the most statistically sound parameter estimates with accurate confidence intervals.
Key Control	Verify <10% substrate depletion at all [S] during the measured time window.	Violation invalidates the initial velocity condition and leads to underestimation of v₀, particularly at low [S].

Critical Considerations for Robust Assay Design

The Scientist's Toolkit: Essential Reagents and Materials

Table 3: Key Research Reagent Solutions for Kinetic Assays [63] [54] [64]

Reagent/Material	Function and Importance	Optimization Considerations
Enzyme (Pure, Active)	The catalyst of interest; source of kinetic parameters. Purity is critical for calculating accurate kcat and specific activity.	Verify purity (SDS-PAGE), confirm absence of contaminating activities. Determine specific activity (units/mg). Ensure lot-to-lot consistency [54].
Substrate (Natural or Surrogate)	The molecule transformed by the enzyme. Defines the reaction being measured.	Use natural substrate if possible. For surrogates (e.g., chromogenic/fluorogenic analogs), validate that kinetics mirror the natural reaction. Chemical purity is essential [54].
Assay Buffer	Maintains optimal pH and ionic strength, stabilizing enzyme conformation and activity.	Systematically optimize pH, buffer species, and ionic strength. Be aware of non-specific buffer effects (e.g., metal chelation) [54].
Cofactors / Cations	Required for the activity of many enzymes (e.g., Mg²⁺ for kinases, NADH for dehydrogenases).	Identify and include all essential cofactors at saturating concentrations during Km determination for the main substrate [54].
Detection Reagents	Enable quantification of reaction progress (e.g., fluorescent dyes, coupled enzymes, antibodies for ELISA).	The detection system must have a linear response over the expected product concentration range and not interfere with the enzymatic reaction [54] [64].
Stabilizers/Carrier Proteins	(e.g., BSA, glycerol). Prevent loss of enzyme activity due to adsorption or instability, especially in dilute solutions.	Test for effects on enzyme activity. They are often crucial for maintaining activity during long assays or with highly diluted enzymes [64].

Signal Detection and Linearity

A fundamental, yet often overlooked, requirement is that the detection system must be linear with respect to product concentration over the entire range generated in the assay. Before kinetic experiments, a standard curve of product versus signal must be performed [54]. If the detector saturates (e.g., absorbance > 3 for a plate reader), the measured velocities will be artificially low, distorting the Michaelis-Menten fit. This is distinct from, but equally important as, ensuring the enzymatic reaction itself is linear with time.

The Logic of Parameter Estimation and Study Design

The mathematical relationship between substrate concentration and velocity has direct implications for experimental design. The sensitivity of the velocity to changes in [S] is greatest when [S] is near the Km. This is why assays designed to discover competitive inhibitors are run at or below the Km—it maximizes the assay's ability to detect a change in velocity caused by the inhibitor competing for the active site [54]. Conversely, to estimate Vmax reliably, data points at substrate concentrations significantly exceeding Km are essential. A study design that only uses low substrate concentrations will yield a poor estimate of Vmax, and vice versa. This principle is vividly illustrated in pharmacokinetics, where estimating the Vmax and Km of a saturable clearance pathway for a monoclonal antibody requires dose groups spanning both the linear and non-linear phases of clearance; using only high or only low doses fails to characterize the Michaelis-Menten curve [62].

Michaelis-Menten Kinetic Model and Equation

Orthogonal Validation and Advanced Applications

Once kinetic parameters are established under optimized conditions, the assay protocol can be applied to screen enzyme variants or potential inhibitors [63]. For high-throughput screening (HTS), assays are often run at a single, fixed substrate concentration (e.g., at or below the Km). The robustness of the HTS assay is frequently evaluated using metrics like the Z′-factor, which accounts for the dynamic range between positive and negative controls and their data variability [65].

Finally, orthogonal validation is a mark of rigorous enzymology. Kinetic parameters derived from a convenient colorimetric assay should be confirmed using a different, direct detection method. For example, a defluorination reaction monitored by pH change can be validated by directly measuring fluoride ion release with an ion-selective electrode or by quantifying substrate loss and product formation via LC-MS/MS [63]. This step confirms that the measured signal truly reflects the intended catalytic event and not an assay artifact.

Reliable estimation of Vmax and Km is not an automatic outcome of any enzyme assay; it is the specific product of a deliberate and systematic optimization process. This process begins with a clear understanding of Michaelis-Menten principles and the non-negotiable requirement for initial velocity conditions. It proceeds through iterative experimental steps to define the linear assay window, the proportional enzyme concentration range, and finally, a comprehensive substrate concentration series for non-linear regression fitting. By adhering to these guidelines, researchers can generate kinetic data with high precision and accuracy, forming a solid quantitative foundation for downstream applications in enzyme engineering, drug discovery, and systems biology modeling.

The accurate estimation of Michaelis-Menten parameters, Vmax and Km, constitutes a foundational objective in enzymology with profound implications for basic research, drug discovery, and metabolic engineering. The canonical Michaelis-Menten equation, derived using the standard quasi-steady-state approximation (sQSSA), has served as the cornerstone of enzyme kinetics for over a century [66]. However, its validity is intrinsically bound to the condition that the total enzyme concentration ([E]T) is significantly lower than the sum of the substrate concentration and the Michaelis constant (Km + [S]T) [15]. This requirement frequently fails in physiological and engineered systems, where enzymes and substrates—particularly in protein interaction networks—often exist in comparable concentrations [67]. The resulting parameter estimation biases undermine the predictive modeling of cellular metabolism and the rational design of therapeutic enzyme inhibitors.

This whitepaper frames the Total Quasi-Steady-State Approximation (tQSSA) as a critical methodological advancement within the broader thesis of robust Vmax and Km estimation research. By redefining the quasi-steady-state variable to include the enzyme-substrate complex, the tQSSA extends accurate kinetic analysis to regimes of high enzyme concentration, thereby bridging the gap between in vitro assays and in vivo reality [15] [67]. The following sections provide a technical guide to the theory, validation, and practical application of tQSSA-based models, equipping researchers with the tools to achieve unbiased, precise parameter estimation across a wider experimental and biological design space.

Theoretical Foundations: From Standard to Total QSSA

The fundamental enzyme reaction mechanism involves the reversible binding of enzyme (E) and substrate (S) to form a complex (C), which subsequently yields product (P) and free enzyme: E + S ⇌ C → E + P [15].

The traditional sQSSA assumes that the concentration of the complex C reaches a steady state rapidly, while the substrate S depletes slowly. This leads to the familiar Michaelis-Menten rate equation: v = (d[P]/dt) = (k_cat * [E]_T * [S]) / (K_M + [S]), where K_M = (k_off + k_cat)/k_on [66]. The critical validity condition for this approximation is [E]_T / (K_M + [S]_T) << 1 [15], which is often violated.

The tQSSA, introduced by Borghans, De Boer, and Segel, circumvents this limitation by defining a new total substrate variable: [Ŝ] = [S] + [C] [66] [67]. The derivation considers the conservation laws ([E]_T = [E] + [C] and [Ŝ] = [S] + [C]) and applies the quasi-steady-state assumption to the complex in terms of these totals. The resulting rate equation is: d[P]/dt = k_cat * [C], where [C] is given by the root of a quadratic equation: [C] = (1/2) * ( [E]_T + K_M + [Ŝ] - sqrt( ([E]_T + K_M + [Ŝ])^2 - 4*[E]_T*[Ŝ] ) ) [15].

A highly accurate and simpler Padé approximant is often used: d[P]/dt ≈ (k_cat * [E]_T * [Ŝ]) / (K_M + [Ŝ] + [E]_T) [67]. This formulation remains valid under a much broader condition, related to the timescale separation between complex dissociation and catalysis, and is reliable even when [E]_T and [S]_T are comparable [67].

• Diagram: Comparison of QSSA Approaches and Their Validity Domains

Table 1: Comparative Validity Conditions for QSSA Approaches

Approximation	Key Variable	Validity Condition	Primary Application Context	Parameter Bias if Violated
Standard QSSA (sQSSA)	Free Substrate [S]	[E]_T ≪ K_M + [S]_T [15]	Traditional in vitro assays with low enzyme concentration.	Significant bias in estimated K_M and k_cat when [E]_T is high [15].
Total QSSA (tQSSA)	Total Substrate [Ŝ] = [S] + [C]	(k_off / k_cat) >> 1 or more general condition [67].	High [E]_T systems, protein interaction networks [67], in vivo modeling.	Minimal bias across all concentration ranges when its condition is met [15].

Quantitative Advantages: Unbiased Parameter Estimation

The primary advantage of the tQSSA framework is its ability to provide unbiased estimates of V_max (and thus k_cat) and K_M from progress curve data, regardless of the initial enzyme-to-substrate ratio [15]. This allows for more flexible and informative experimental designs.

Table 2: Performance Comparison of sQSSA vs. tQSSA in Parameter Estimation [15]

Estimation Context	Model Used	Estimation Bias	Experimental Design Implication
Low [E]T / (KM+[S]_T)	sQSSA (Michaelis-Menten)	Negligible	Requires careful setup to ensure low enzyme concentration, often needing prior knowledge of ~K_M.
High [E]T / (KM+[S]_T)	sQSSA (Michaelis-Menten)	High, potentially severe	Leads to incorrect parameters if used; common pitfall in physiologically-relevant modeling.
Any [E]T / [S]T ratio	tQSSA	Consistently Low	Enables pooling of progress curve data from experiments with different [E]_T and [S]_T to improve precision.
Optimal Design from Scatter Plots	tQSSA (Bayesian)	Minimal	The next optimal experiment to reduce parameter uncertainty can be identified without prior K_M knowledge [15].

A Bayesian inference approach using the tQSSA model has been shown to accurately and precisely estimate parameters for enzymes with disparate catalytic efficiencies (e.g., chymotrypsin, fumarase, urease) from minimal time-course data [15]. This method effectively resolves the parameter identifiability problem often encountered with the sQSSA model, where highly correlated estimates for K_M and V_max can fit the data well but be far from their true values.

Critical Considerations for Stochastic and Networked Systems

The deterministic accuracy of the tQSSA has led to its perceived universal validity in stochastic model reduction. However, recent research (2025) demonstrates that applying the tQSSA-derived propensity functions in stochastic simulations of biochemical reaction networks can distort dynamics, even when the deterministic approximation is excellent [68]. This highlights a critical distinction: a model's accuracy in deterministic simulations does not guarantee its correctness in stochastic ones. Therefore, caution is required when using deterministic QSSAs for stochastic model reduction to avoid erroneous conclusions about noise-driven phenomena [68].

Conversely, for deterministic modeling of networks of coupled enzymatic reactions, such as protein kinase/phosphatase cascades in signaling pathways, the tQSSA is not only valid but essential. In these protein interaction networks (PINs), proteins act as both enzymes and substrates for each other, making the low-enzyme condition of the sQSSA impossible for all reactions simultaneously [67]. The tQSSA successfully captures the dynamics of modules like the Goldbeter-Koshland switch and complex feedback networks, whereas the classic Michaelis-Menten formalism fails qualitatively and quantitatively [67].

• Diagram: Application Domains of tQSSA in Biochemical Modeling

Table 3: Guidelines for Applying tQSSA in Different Contexts

Research Context	Recommended Use of tQSSA	Key Rationale & Caveats
Deterministic Modeling of Protein Networks	Essential. Use tQSSA-derived rate laws [67].	Enzymes and substrates are in comparable concentrations; sQSSA fails.
Stochastic Simulation of Reaction Networks	Apply with caution. Requires validation against full model [68].	tQSSA propensity functions may distort noise characteristics even if deterministic fit is good.
Parameter Estimation (Progress Curve)	Highly recommended, especially if [E]_T is unknown or high. Use Bayesian framework [15].	Provides unbiased estimates across all concentration ranges; enables optimal experimental design.
Classical Initial Velocity Assay	May not be necessary if low [E]_T is rigorously verified.	Linear transforms (Lineweaver-Burk) are based on sQSSA; tQSSA offers no advantage if its condition is met.

Experimental Protocols for tQSSA-Based Parameter Estimation

Implementing tQSSA-based analysis requires careful experimental execution. The following protocol, synthesized from best practices in enzymology and tQSSA literature, ensures reliable data collection for robust parameter inference [63] [15].

• Diagram: Experimental Workflow for tQSSA-Based Kinetic Characterization

Protocol: Comprehensive Enzyme Kinetics Using tQSSA

Objective: To accurately determine the kinetic parameters k_cat and K_M of an enzyme using progress curve analysis under conditions valid for the tQSSA, including high enzyme concentrations.

Materials:

• Purified enzyme at known concentration (multiple aliquots at different concentrations recommended).
• Substrate stock solutions across a concentration range (e.g., 0.1x to 20x expected K_M).
• Appropriate assay buffer.
• Detection system: plate reader (for colorimetric/pH-based assays), ion-selective electrode, or stopped-flow spectrophotometer for rapid kinetics [63].
• Quenching solution if using discontinuous sampling (e.g., for LC-MS/MS validation [63]).

Procedure:

• Define Experimental Matrix: Design experiments that vary both total enzyme concentration ([E]_T) and total initial substrate concentration ([Ŝ]_0). Include conditions where [E]_T is similar to or greater than [Ŝ]_0 and expected K_M [15].
• Establish Linear Phase: For each [E]_T, perform pilot reactions at low, medium, and high [Ŝ]_0. Take frequent initial timepoints (e.g., every 5-10 seconds) to identify the time window where product formation is linear with time. Ensure subsequent progress curve data captures this initial linear phase [63].
• Execute Progress Curve Assays: In triplicate, initiate reactions for all combinations in your experimental matrix. Continuously monitor product formation (e.g., in a plate reader) or take aliquots at defined timepoints and quench immediately. Collect data until substrate is nearly depleted or the curve clearly plateaus [15].
• Orthogonal Validation (Optional but Recommended): For key conditions, confirm product formation using a direct chemical method (e.g., fluoride ion electrode for dehalogenases [63] or LC-MS/MS [63]). This validates that the observed signal corresponds to the correct biochemical transformation.

Data Analysis:

• Global Nonlinear Fitting: Fit the ensemble of progress curve data ([P] vs. t for all [E]_T and [Ŝ]_0) simultaneously to the integrated form of the tQSSA rate equation (Equation 2) [15] using computational software (e.g., Python, R, MATLAB, or provided packages [15]).
• Bayesian Inference (Advanced): Implement a Bayesian inference framework to estimate posterior distributions for k_cat and K_M. This approach naturally handles parameter uncertainty and identifiability, and allows for the design of optimal subsequent experiments [15].
• Model Comparison: Compare the fit of the tQSSA model against the sQSSA (Michaelis-Menten) model using statistical criteria (e.g., AIC, residuals analysis). Significant improvement with the tQSSA model indicates the sQSSA condition was violated.

Table 4: Research Reagent Solutions for tQSSA-Optimized Kinetics

Reagent / Material	Function in tQSSA Context	Key Considerations
High-Purity Enzyme Preps	Provides accurate [E]_T for high-concentration regimes.	Activity must be verified; concentration determined by A280 or quantitative assay. Essential for the [E]_T term in tQSSA equations.
Stable, Quantifiable Substrates	Enables precise knowledge of initial [Ŝ]_0.	Solubility at high concentrations (needed for high [E]_T tests) is critical. Use of radiolabeled or fluorophore-tagged substrates can enhance detection sensitivity.
Rapid-Kinetics Stopped-Flow Instrument	Captures initial linear velocity at very high [E]_T where reactions may be extremely fast.	Necessary for enzymes with high k_cat to avoid missing the initial linear phase [63].
Orthogonal Detection Kits (e.g., Fluoride Probe, LC-MS)	Validates that the primary assay signal (e.g., pH change) corresponds to correct product formation [63].	Crucial for confirming assay fidelity, especially when using indirect detection methods under novel high [E]_T conditions.
TISAB Buffer (for ion probes)	Stabilizes ionic strength and complexes interfering ions when using ion-selective electrodes [63].	Ensures accurate quantitation of ions like fluoride released from enzymatic defluorination.
Bayesian Inference Software Package	Performs accurate parameter estimation from progress curves using the tQSSA model [15].	The provided package [15] or custom scripts in Stan/PyMC3 are needed to implement the recommended analysis.
Computational Model for Network Simulation	Simulates dynamics of coupled enzymatic networks (PINs) using tQSSA rate laws [67].	Software like COPASI, Virtual Cell, or custom ODE solvers must implement the tQSSA equations, not just MM kinetics.

The Total Quasi-Steady-State Approximation represents a necessary evolution in the quantitative analysis of enzyme kinetics, directly addressing the limitations of the century-old Michaelis-Menten framework in modern biological contexts. By enabling accurate Vmax and Km estimation under high enzyme concentrations and in protein interaction networks, the tQSSA strengthens the core thesis of rigorous parameter estimation research. Its integration with Bayesian inference frameworks further provides a statistically powerful method for experiment design and parameter identifiability [15].

Future advancements lie at the intersection of this refined kinetic theory with emerging technologies. The development of deep learning models (e.g., DLERKm [69]) for predicting kinetic parameters from sequence and reaction data could be enhanced by training on tQSSA-derived, unbiased parameter sets. Furthermore, the cautionary note on stochastic applications [68] opens a research avenue to develop and validate reduced stochastic models that retain the accuracy of the tQSSA. For researchers and drug developers, adopting the tQSSA paradigm is no longer a specialist consideration but a best practice for ensuring that kinetic parameters—the foundational constants of enzymatic function—are derived with the fidelity demanded by contemporary systems biology and precision medicine.

Accurate estimation of enzyme kinetic parameters—specifically the maximum reaction velocity (Vmax) and the Michaelis constant (Km)—is a cornerstone of quantitative biochemistry with profound implications for drug discovery and development [70]. These parameters are essential for understanding metabolic stability, predicting drug-drug interactions, and optimizing therapeutic dosing, such as in the case of drugs like phenytoin which exhibit capacity-limited kinetics [71]. Traditionally, experimental designs for estimating Vmax and Km have been based on empirical conventions, often involving arbitrary selections of substrate concentrations and sampling times [72]. However, these traditional approaches can be inefficient, resource-intensive, and may yield parameter estimates with unacceptably high variability [73] [74].

This whitepaper, framed within the broader thesis of advancing Vmax and Km estimation research, elucidates the principles and applications of optimal experimental design (OED). OED employs statistical and computational strategies to a priori determine the most informative experimental conditions—specifically, the selection of multiple starting concentrations (C0) and optimal sampling time points [75]. The core objective is to maximize the precision of parameter estimates (minimize standard error) while constraining resources such as the total number of samples, incubation time, and compound material [72]. By moving beyond one-factor-at-a-time approaches, OED provides a robust framework for generating high-quality kinetic data more efficiently, thereby accelerating screening processes and enhancing the reliability of mechanistic models in drug metabolism [59].

Methodological Approaches to Optimal Design

Optimal experimental design for enzyme kinetics formalizes the selection of experimental variables to minimize the expected statistical uncertainty in the estimated parameters. The following key methodologies have been developed and validated in the literature.

Penalized ED-Optimal Design for Screening

For high-throughput screening environments, a penalized expectation-of-determinant (ED)-optimal design has been successfully implemented [75] [74]. This approach uses a discrete prior distribution of probable Km and Vmax values (e.g., from historical data on 76 compounds) to find a general, pragmatic design applicable to new compounds without prior kinetic knowledge [72].

• Design Constraints: The optimization is typically bounded by practical limits: a maximum of 15 samples per compound, an incubation time of up to 40 minutes, and starting concentrations (C0) ranging from 0.01 to 100 µM [75].
• Optimization Output: The algorithm identifies the combination of 3-4 optimal starting concentrations and corresponding sampling time points that minimize the predicted standard error (S.E.) for CLint, Vmax, and Km estimates [72]. A common finding is the inclusion of both high and low C0 values and a strong recommendation for a terminal sample at the latest possible time (e.g., 40 min) to best characterize the depletion curve [72].
• Performance: When simulated against a standard design (single C0 of 1 µM with fixed time points), this OED generated a lower relative standard error for 99% of compounds and provided high-quality estimates (RMSE < 30%) for both Vmax and Km for 26% of investigated compounds [74].

The 50-BOA for Enzyme Inhibition Studies

A recent, innovative advance in OED is the IC50-Based Optimal Approach (50-BOA) for enzyme inhibition studies [76]. This method dramatically simplifies the experimental burden for estimating inhibition constants (Kic and Kiu).

• Principle: The 50-BOA leverages the mathematical relationship between the half-maximal inhibitory concentration (IC50) and the inhibition constants. Analysis of the estimation error landscape revealed that experiments using inhibitor concentrations (IT) below the IC50 provide little information for distinguishing between inhibition mechanisms, while data from a single IT greater than the IC50 is sufficient for precise estimation [76].
• Protocol: Researchers first perform a preliminary experiment to estimate the IC50 at a single substrate concentration (often near Km). Subsequently, initial velocity (V0) is measured at multiple substrate concentrations (e.g., 0.2Km, Km, 5Km) but at only one optimized inhibitor concentration (IT > IC50) [76].
• Efficiency: This approach reduces the required number of experimental conditions by over 75% compared to the canonical method requiring a full matrix of substrate and inhibitor concentrations, without compromising precision or accuracy [76].

Model-Based Designs via Software Tools

Implementation of these OED strategies is facilitated by specialized software which performs model-based simulations and optimizations.

• PopED: A known software used for population optimal experimental design, capable of handling nonlinear mixed-effects models, suitable for designing enzyme kinetic experiments [72].
• DoE-General Guides: General Design of Experiments (DoE) principles, including fractional factorial designs and response surface methodology, can be applied to assay optimization, helping to efficiently identify significant factors (e.g., pH, buffer ions) affecting enzyme activity in just a few days [59].

The quantitative outcomes from key validation studies of these methodologies are summarized in Table 1 below.

Table 1: Comparative Performance of Optimal vs. Standard Experimental Designs

Design Type	Key Features	Performance Metric	Result	Key Reference
General Penalized ED-Optimal Design	15 samples, 40 min, C0=0.01-100 µM	% Compounds with better RSE vs. STD-D	99%	[74]
		% Compounds with high-quality Vmax/Km (RMSE<30%)	26%	[74]
Optimal Design (OD) Evaluation	Multiple C0, optimal times	CLint within 2-fold of reference method	>90%	[73]
		Vmax/Km within 2-fold of reference method	>80%	[73]
50-BOA for Inhibition	Single IT > IC50	Reduction in required experiments	>75%	[76]

Core Experimental Protocols

This section details step-by-step protocols for implementing two pivotal OED strategies: the general optimal design for depletion kinetics and the 50-BOA for inhibition studies.

Protocol for Depletion Kinetics with Multiple Starting Concentrations

This protocol is adapted for use with human liver microsomes (HLM) to estimate intrinsic clearance (CLint), Vmax, and Km [73].

• Prior Information & Design Selection: Consult a historical database or literature to define a plausible range for Km and Vmax. Use OED software (e.g., PopED) with these priors and your constraints (e.g., max 15 samples, 40 min) to generate an optimal design table specifying, for example, 4 different C0 values (e.g., 0.1, 1, 10, 50 µM) each with 3-4 scheduled sampling times [72].
• Incubation Setup:
  • Prepare a master mix of HLM (e.g., 0.5 mg/mL protein) in potassium phosphate buffer (100 mM, pH 7.4) with MgCl2.
  • Pre-warm the master mix and NADPH-regenerating system at 37°C.
  • In separate incubation vials, spike the master mix with test compound to achieve the four predetermined C0 values.
  • Initiate reactions by adding the NADPH-regenerating system.
• Sample Collection & Quenching: At each predefined optimal time point (e.g., 0, 5, 20, 40 min), withdraw a defined aliquot from each C0 incubation and quench it in an equal volume of acetonitrile containing an internal standard. Centrifuge to precipitate proteins.
• Analysis & Fitting:
  • Analyze supernatant using LC-MS/MS to determine substrate concentration over time for each C0 [73].
  • Fit the combined multi-C0 depletion data directly to the integrated Michaelis-Menten equation using nonlinear regression to obtain simultaneous estimates of Vmax and Km. CLint is derived as Vmax/Km [73] [72].

Protocol for the 50-BOA Inhibition Assay

This protocol outlines the streamlined process for estimating competitive, uncompetitive, or mixed inhibition constants [76].

• Preliminary IC50 Determination:
  • Set up reactions with a fixed substrate concentration near its known Km.
  • Use 6-8 inhibitor concentrations spanning a broad range (e.g., 0.1x to 10x expected potency).
  • Measure initial reaction velocities (V0), plot % control activity vs. [Inhibitor], and fit a sigmoidal curve to estimate the IC50 value.
• Optimal Single-Inhibitor Concentration Experiment:
  • Based on the IC50, select a single inhibitor concentration (IT) where IT > IC50 (e.g., 2x IC50).
  • Set up a matrix of reactions varying the substrate concentration (e.g., at least 6 points spanning 0.2Km to 5Km) in the presence of this single IT. Include control wells without inhibitor.
  • Measure the initial velocity (V0) for all conditions.
• Data Analysis & Fitting:
  • Use provided MATLAB or R packages for the 50-BOA [76].
  • Input the V0 data, substrate concentrations, and the predetermined IC50 value.
  • The algorithm fits the general inhibition model (Equation 1) using the relationship between IC50, Kic, and Kiu as a constraint, yielding precise estimates for both inhibition constants and identifying the inhibition type [76].

The logical workflow integrating both traditional and optimal design concepts is visualized in the following diagram.

Diagram: Comparative Workflow of Traditional and Optimal Experimental Design Strategies

The Scientist's Toolkit: Essential Research Reagents and Materials

Implementing optimal design strategies requires careful selection of reagents and materials. The following table details key components for robust enzyme kinetic studies.

Table 2: Key Research Reagent Solutions for Enzyme Kinetic Studies

Item	Function/Description	Application Notes
Human Liver Microsomes (HLM)	Membrane-bound enzyme fractions containing CYPs and UGTs; the standard in vitro system for Phase I metabolism [73].	Lot-to-lot variability exists. Pooled donors are used for general screening. Specific single-donor HLMs can assess polymorphisms.
NADPH Regenerating System	Supplies constant NADPH, the essential cofactor for CYP450 reactions. Typically includes glucose-6-phosphate, Mg2+, and G6P dehydrogenase [73].	Critical for maintaining linear reaction conditions. A positive control (e.g., testosterone) should be run to verify system activity.
LC-MS/MS System	Gold-standard analytical platform for quantifying substrate depletion or product formation with high sensitivity and specificity [73].	Enables multiplexing and cassette analyses. Requires stable isotope-labeled or structural analog internal standards for optimal precision.
Optimal Design Software (e.g., PopED)	Computational tool for pre-experiment simulation and optimization of sampling schedules and concentration levels [72].	Requires definition of a prior parameter distribution and a pharmacokinetic/pharmacodynamic (PK/PD) model (e.g., Michaelis-Menten).
Specific Enzyme/Protein	The purified enzyme or cellular overexpression system of interest (e.g., recombinant CYP3A4, HRV-3C protease) [76] [59].	Essential for mechanistic inhibition studies or non-microsomal enzymes. Purity and activity must be characterized.

Data Analysis, Interpretation, and Future Directions

Analysis of Data from Optimal Designs

Data generated from OED protocols require appropriate analytical techniques. While nonlinear regression fitting to the integrated Michaelis-Menten model is paramount [73], linear transformations remain useful for visualization and initial estimates:

• Eadie-Hofstee Plot (V vs. V/[S]): Useful for identifying deviations from standard kinetics; slope = -Km, y-intercept = Vmax [71] [77].
• Direct Linear Plot: A robust, non-parametric method where pairs of ([S], V) define lines whose intersection region estimates Vmax and Km [71].

A critical advantage of OED is that it provides not only parameter estimates but also a lower predicted parameter uncertainty. This allows for more reliable classification of compounds (e.g., high vs. low clearance, competitive vs. mixed inhibitor) and more confident predictions of in vivo outcomes [76] [74].

Future Directions and Integration

The field of efficient experimental design is evolving rapidly. Key future directions include:

• AI-Driven Adaptive Designs: Machine learning algorithms could analyze preliminary data in real-time to dynamically recommend the next optimal sampling point or concentration, further maximizing information gain.
• High-Throughput Automation Integration: OED principles are ideally suited for robotic liquid handling and automated screening platforms, where predefined optimal plans can be executed with precision [59].
• Expanded Scope to Complex Systems: Applying OED to more complex in vitro systems, such as hepatocytes or tissue models, and to model mechanisms beyond simple Michaelis-Menten kinetics (e.g., autoactivation, substrate inhibition).

The paradigm-shifting 50-BOA method, which fundamentally rethinks the requirements for inhibition studies, serves as a template for this future innovation [76]. Its underlying principle—mapping the error landscape of parameter estimation to identify minimally sufficient, highly informative experimental conditions—is applicable to a wide range of biochemical characterization problems. The synergistic relationship between traditional characterizations, optimal design, and next-generation methods is illustrated below.

Diagram: Evolution and Application of Efficient Experimental Design Methodologies

In conclusion, the strategic use of multiple starting concentrations and optimal sampling times, guided by model-based optimal experimental design principles, represents a significant leap forward in enzyme kinetics research. By increasing the precision of Vmax and Km estimates while reducing experimental burden, these strategies directly enhance the efficiency and reliability of drug metabolism and safety assessment, forming a critical component of modern, rational drug development.

Validating Results and Comparing Methodologies in Vmax and Km Estimation

This whitepaper examines the critical importance of cross-method validation for accurate estimation of Michaelis-Menten kinetic parameters, Vmax and Km. Within the broader context of enzymology and drug development research, we demonstrate that traditional linearization methods, while historically useful, introduce significant statistical bias and error distortion. Contemporary nonlinear regression, Bayesian inference, and machine learning-aided techniques offer superior accuracy and precision, particularly under realistic experimental error structures. We present a consolidated framework integrating simulation-based validation, advanced computational tools, and multi-method consensus to ensure reliable and reproducible kinetic parameter estimation, which is foundational for robust biochemical modeling and therapeutic development.

The estimation of the maximum reaction rate (Vmax) and the Michaelis constant (Km) from the Michaelis-Menten equation is a cornerstone of quantitative biochemistry, pharmacology, and drug development [44]. These parameters are not merely fitting constants; they provide fundamental insights into enzyme efficiency, substrate affinity, and the catalytic mechanism. In drug discovery, accurate determination of these constants is essential for characterizing drug metabolism, assessing drug-drug interaction potentials, and understanding inhibitory mechanisms of novel therapeutic compounds [78].

Historically, linear transformations of the Michaelis-Menten equation, such as the Lineweaver-Burk (double reciprocal), Eadie-Hofstee, and Hanes-Woolf plots, have been the standard tools for estimating Vmax and Km due to their computational simplicity [22] [35]. However, these linearization methods possess a critical flaw: they distort the error structure of the original data. By applying transformations like taking the reciprocal of the reaction velocity, the assumptions of homoscedasticity (constant variance) required for ordinary linear regression are violated. This leads to overweighting of data points at low substrate concentrations, resulting in biased and imprecise parameter estimates [44] [35] [43].

The advancement of computational power has made nonlinear regression techniques—which fit the untransformed data directly to the Michaelis-Menten model—accessible and statistically preferable [44] [15]. More recently, sophisticated approaches incorporating Bayesian inference, progress curve analysis with more accurate mathematical approximations, and machine learning have emerged to address limitations in classical assays and parameter identifiability [15] [79]. This evolution creates a landscape where multiple estimation techniques coexist, necessitating a formalized approach to cross-method validation. Ensuring consistency across these diverse techniques is paramount for generating reliable kinetic parameters that can be confidently used in predictive modeling and critical decision-making in research and development.

Core Methodologies for Parameter Estimation

This section details the primary experimental and computational methods used for estimating Vmax and Km, ranging from classical linearization to state-of-the-art computational techniques.

Traditional Linearization Methods

These methods algebraically manipulate the Michaelis-Menten equation into a linear form.

• Lineweaver-Burk (Double Reciprocal) Plot: The most widely recognized linearization, where the reciprocal of velocity (1/v) is plotted against the reciprocal of substrate concentration (1/[S]). The y-intercept is 1/Vmax, the x-intercept is -1/Km, and the slope is Km/Vmax [22] [35]. Its primary drawback is severe distortion of experimental error, giving undue influence to less precise measurements at low [S] [35] [43].
• Eadie-Hofstee Plot: Plots v against v/[S]. The slope is -Km, the y-intercept is Vmax, and the x-intercept is Vmax/Km [44] [78]. While error distortion is different from the Lineweaver-Burk plot, it still violates assumptions of standard linear regression.
• Hanes-Woolf Plot: Plots [S]/v against [S]. The slope is 1/Vmax, the y-intercept is Km/Vmax, and the x-intercept is -Km [78]. It offers better error properties than the Lineweaver-Burk plot but remains inferior to direct nonlinear fitting.

Direct Nonlinear Regression (NLR)

This approach fits the untransformed velocity vs. [S] data directly to the Michaelis-Menten equation using iterative algorithms (e.g., Levenberg-Marquardt) to minimize the sum of squared residuals. It preserves the original error structure and is currently considered the standard for accurate parameter estimation from initial velocity data [44]. Software such as GraphPad Prism, R, and Python libraries (SciPy) commonly implement this method.

Progress Curve Analysis with Advanced Kinetic Models

Instead of relying on initial velocity measurements, this method fits the entire time course of substrate depletion or product formation to an integrated rate equation.

• Standard Quasi-Steady-State (sQ) Model: Based on the classic Michaelis-Menten equation, valid only under the condition that the total enzyme concentration is much lower than the sum of the substrate concentration and Km [15].
• Total Quasi-Steady-State (tQ) Model: A more robust approximation derived using the total QSSA, which remains accurate even when enzyme concentration is not negligible compared to substrate [15]. A Bayesian inference framework based on the tQ model has been shown to yield unbiased estimates across a wider range of experimental conditions [15].

Machine Learning & Hybrid Global Optimization

• Machine Learning-Aided Global Optimization (MLAGO): This hybrid method first uses a machine learning model (trained on features like EC number and compound ID) to predict a biologically plausible prior estimate for Km. This prediction is then used to constrain a subsequent global optimization process that fits the kinetic model to experimental data. This approach reduces computational cost, avoids unrealistic parameter values, and helps overcome parameter non-identifiability issues [79].
• Physics-Informed Neural Networks (PINNs): Advanced deep learning frameworks like PINNs and their variants (e.g., cd-PINN) are being explored to solve the ordinary differential equations governing enzyme kinetics. These can potentially learn solution operators that generalize across different kinetic parameters and initial conditions [80].

Quantitative Comparison of Estimation Methods

The following tables synthesize data from simulation studies that quantitatively compare the performance of different Vmax and Km estimation techniques.

Table 1: Performance of Estimation Methods from Monte Carlo Simulation [44] Study based on 1000 replicates of simulated invertase kinetics (True Vmax = 0.76 mM/min, True Km = 16.7 mM).

Estimation Method	Error Model	Median Vmax (90% CI)	Median Km (90% CI)	Key Performance Note
Lineweaver-Burk (LB)	Additive	0.77 (0.70, 0.84)	18.2 (13.8, 23.6)	Low precision, biased.
Eadie-Hofstee (EH)	Additive	0.76 (0.70, 0.83)	17.3 (13.4, 22.5)	Moderate precision.
Nonlinear (NL) on v-[S]	Additive	0.76 (0.73, 0.79)	16.8 (14.5, 19.4)	Accurate and precise.
Nonlinear on [S]-time (NM)	Additive	0.76 (0.75, 0.77)	16.7 (15.9, 17.5)	Most accurate and precise.
Lineweaver-Burk (LB)	Combined	0.78 (0.68, 0.90)	19.8 (13.1, 30.5)	Poor performance, high bias.
Nonlinear on [S]-time (NM)	Combined	0.76 (0.75, 0.78)	16.8 (15.9, 17.8)	Robust to complex error.

Table 2: Model Validity Conditions for Progress Curve Analysis [15] Comparison of the foundational assumptions for two major kinetic models used in progress curve fitting.

Model	Governing Equation (dP/dt)	Key Validity Condition	Primary Limitation
Standard QSSA (sQ) Model	k_cat * E_T * (S_T - P) / (K_M + S_T - P)	E_T / (K_M + S_T) << 1 (Low enzyme concentration)	Fails when enzyme concentration is high, leading to biased estimates.
Total QSSA (tQ) Model	k_cat * [E_T + K_M + S_T - P - sqrt((E_T+K_M+S_T-P)^2 - 4*E_T*(S_T-P))] / 2	Generally valid for a wider range of conditions.	More computationally complex, but enables accurate estimation under high E_T.

Experimental Protocols for Cross-Method Validation

A robust cross-method validation strategy involves generating high-quality data and analyzing it through multiple independent estimation pipelines.

Protocol: Simulation-Based Method Benchmarking

This protocol, adapted from a published simulation study, provides a template for objectively comparing estimation methods [44].

• Define Reference Parameters: Establish true kinetic parameters (Vmax, Km) based on literature for a well-characterized enzyme (e.g., invertase: Vmax=0.76 mM/min, Km=16.7 mM) [44].
• Generate Error-Free Time-Course Data: Use an ODE solver (e.g., deSolve package in R) to simulate substrate depletion over time for multiple initial substrate concentrations ([S]0) using the Michaelis-Menten equation: d[S]/dt = - (Vmax * [S]) / (Km + [S]).
• Introduce Experimental Error: Create multiple replicate datasets (e.g., 1000) by adding random noise to the error-free data. Test different error models:
  • Additive: [S]obs = [S]pred + ε, where ε ~ N(0, σ).
  • Combined: [S]obs = [S]pred + ε1 + [S]pred * ε2, where ε1, ε2 ~ N(0, σ) [44].
• Apply Diverse Estimation Methods:
  • Linearization: Calculate initial velocities (v) from early time points. Generate transformed data for Lineweaver-Burk (1/v vs. 1/[S]) and Eadie-Hofstee (v vs. v/[S]) plots. Perform linear regression.
  • Direct Nonlinear Regression (NL): Fit the v vs. [S] data directly to the Michaelis-Menten equation using nonlinear least squares (e.g., in R or NONMEM).
  • Progress Curve Nonlinear Regression (NM): Fit the full [S]-time data directly to the integrated Michaelis-Menten ODE using software like NONMEM [44].
• Analyze and Compare Outcomes: For each method and replicate, extract estimated Vmax and Km. Compare distributions of estimates to true values using metrics like median bias, 90% confidence intervals, and root-mean-square error.

Protocol: Bayesian Progress Curve Analysis using the tQ Model

This protocol leverages a more accurate kinetic model for parameter estimation from progress curve data [15].

• Experimental Data Collection: Conduct a reaction progress curve assay, measuring product concentration over time. Ideally, include conditions with varying initial enzyme and substrate concentrations.
• Model Specification: Employ the tQ model (see Table 2), which is valid for a broader range of enzyme concentrations than the standard model.
• Bayesian Inference Setup:
  • Define prior distributions for parameters (kcat, KM). Use weak, informative priors if no strong prior knowledge exists.
  • Define a likelihood function, assuming a normal or log-normal distribution for the experimental measurement error.
• Parameter Estimation: Use a Markov Chain Monte Carlo (MCMC) sampling tool (e.g., Stan, PyMC) to obtain the posterior distributions for kcat and KM. Note: Vmax = kcat * ET.
• Validation: Assess model fit by examining posterior predictive checks. Compare estimates with those obtained from the standard sQ model to evaluate bias, especially in experiments where E_T is not negligible.

Visualizing the Validation Workflow and Kinetic Ecosystem

Cross-Method Validation Workflow for Km/Vmax Estimation

Michaelis-Menten Kinetic Parameter Estimation Ecosystem

The Scientist's Toolkit: Essential Research Reagent Solutions

Table 3: Key Reagents, Software, and Tools for Kinetic Studies & Cross-Method Validation

Item	Function / Purpose in Validation	Example / Sourcing Information
Well-Characterized Enzyme	Serves as a positive control or reference system for benchmarking estimation methods.	Invertase (used in simulation studies [44]), 11β-HSD1 (for inhibition studies [78]).
Specific Inhibitor	Used to study inhibition mechanisms and test method performance under different kinetic regimes (e.g., competitive, mixed).	Bisphenol Z (BPZ) as a mixed inhibitor of 11β-HSD1 [78].
High-Precision Analytical Instrument	For accurate measurement of substrate depletion or product formation over time (progress curve).	UPLC system with gradient elution capability (e.g., Acquity UPLC BEH C18 column) [78].
Statistical & Modeling Software (R/Python)	Core platform for data simulation, nonlinear regression, and implementing custom validation scripts.	R with packages deSolve, drc, nlmrt. Python with SciPy, PyMC, TensorFlow/PyTorch for PINNs.
Pharmacokinetic/Pharmacodynamic (PK/PD) Software	For robust ODE-based fitting of progress curve data using advanced estimation algorithms.	NONMEM [44], Monolix, ADAPT.
Bayesian Inference Tool	To implement tQ model-based progress curve analysis and quantify parameter uncertainty.	Stan (via rstan or pystan), PyMC [15].
Machine Learning Framework	To explore hybrid prediction-optimization methods like MLAGO or neural ODE solvers.	Scikit-learn for MLAGO initial predictor [79], PyTorch for developing cd-PINN [80].

Discussion and Best Practices for Reliable Estimation

The convergence of evidence from simulation and empirical studies is clear: nonlinear methods consistently outperform traditional linear transformations in both accuracy and precision [44] [43]. The linearization step, particularly in the Lineweaver-Burk plot, distorts error structure and should be avoided for definitive parameter estimation. Its primary utility remains in educational settings and for the qualitative diagnosis of inhibition types [22] [35].

For robust, research-grade parameter estimation, the following best practices are recommended:

• Prioritize Direct Nonlinear Regression: For initial velocity data, use weighted nonlinear least squares fitting to the Michaelis-Menten equation as the default method.
• Embrace Progress Curve Analysis: Where feasible, collect full time-course data. Fit this data using the integrated form of the Michaelis-Menten equation or, better yet, the more general tQ model, especially if enzyme concentration is not guaranteed to be very low [15].
• Quantify and Report Uncertainty: Move beyond point estimates. Report confidence intervals from nonlinear regression or credible intervals from Bayesian analysis. Use simulation-based error models (additive, proportional, combined) to assess estimator robustness during method development [44].
• Implement Cross-Method Validation as a Standard: Report estimates from at least two independent methods (e.g., nonlinear regression on initial velocities and ODE-based progress curve fitting). Significant discrepancies should trigger investigation into data quality or model misspecification.
• Leverage Computational Advances Judiciously: Machine learning priors (MLAGO) can constrain optimization to biologically realistic spaces [79]. Advanced neural ODE solvers (cd-PINN) show promise for generalizable solutions but must be validated against established numerical methods [80] [81].

Within the critical research domain of Vmax and Km estimation, cross-method validation is not a mere technical formality but a necessary safeguard against methodological bias. The historical reliance on linear transformations has been superseded by statistically sound nonlinear and computational techniques. A modern validation framework integrates careful experimental design, simulation-based benchmarking, and the application of multiple independent estimation pipelines—spanning classical nonlinear regression, Bayesian progress curve analysis, and machine learning-aided optimization. By adopting this consensus-driven approach, researchers in drug development and basic enzymology can ensure the kinetic parameters that underpin their models and hypotheses are accurate, precise, and reproducible, thereby strengthening the foundation of translational biochemical science.

The accurate determination of enzyme kinetic parameters, namely the maximum reaction rate (Vmax) and the Michaelis constant (Km), constitutes a foundational pillar in biochemical, pharmacological, and drug development research [28]. These parameters are indispensable for characterizing enzyme function, modeling metabolic pathways, predicting in vivo drug clearance, and designing dosage regimens [82] [15]. The Michaelis-Menten equation, V = (Vmax * [S]) / (Km + [S]), elegantly describes this relationship but presents a significant challenge: it is inherently nonlinear in its parameters [28].

Traditionally, researchers have relied on linear transformation methods, such as the Lineweaver-Burk and Eadie-Hofstee plots, to simplify estimation. However, these methods distort error structures and can yield biased, imprecise estimates [28]. In contrast, modern computational approaches, particularly nonlinear regression and Bayesian estimation, directly fit the untransformed model to data. Bayesian methods offer a probabilistic framework that quantifies uncertainty, incorporates prior knowledge, and provides robust estimates even with complex error models or limited data [83] [15].

This whitepaper provides a comprehensive technical evaluation of these two paradigms within the context of Vmax and Km estimation research. We dissect their methodological foundations, compare their accuracy and precision through simulated and empirical data, and provide detailed protocols for implementation, empowering researchers to select the optimal tool for their kinetic analyses.

Methodological Foundations and Comparative Framework

Traditional Linearization Methods

Traditional methods linearize the Michaelis-Menten equation for analysis with simple linear regression.

• Lineweaver-Burk (Double Reciprocal) Plot: Transforms the equation into 1/V = (Km/Vmax) * (1/[S]) + 1/Vmax. While intuitive, this plot disproportionately amplifies errors at low substrate concentrations ([S]), often leading to poor parameter estimates [28].
• Eadie-Hofstee Plot: Uses the form V = Vmax - Km * (V/[S]). It provides better error weighting than Lineweaver-Burk but can still be problematic when the V/[S] term contains significant error [28].

The core limitation of these methods is their violation of the fundamental assumptions of linear regression—namely, homoscedasticity (constant variance) of the transformed data [28].

Modern Bayesian Estimation Methods

Bayesian estimation treats unknown parameters (Vmax, Km) as random variables with probability distributions [83]. The process involves:

• Prior Distribution (P(θ)): Encodes existing knowledge or beliefs about the parameters before observing the new experimental data. This can be non-informative (e.g., a broad uniform distribution) or informative based on literature [83].
• Likelihood (P(Data|θ)): Represents the probability of observing the experimental data given specific parameter values, defined by the chosen kinetic model (e.g., Michaelis-Menten with a specified error model) [15].
• Posterior Distribution (P(θ|Data)): The final outcome, computed via Bayes' Theorem: Posterior ∝ Likelihood × Prior. This distribution fully characterizes parameter estimates and their uncertainty [83].

Advanced sampling techniques like Markov Chain Monte Carlo (MCMC) are used to compute the posterior distribution, especially for complex, non-linear models [10] [83]. This framework naturally handles complex error structures and allows for the direct incorporation of hierarchical data (e.g., multiple enzyme batches or patient populations).

Table 1: Core Conceptual Comparison of Estimation Paradigms

Feature	Traditional Linearization	Modern Bayesian Estimation
Philosophical Basis	Frequentist; parameters are fixed unknowns.	Probabilistic; parameters have distributions.
Error Handling	Often violates regression assumptions after transformation.	Explicitly models error structure within the likelihood.
Prior Knowledge	Cannot formally incorporate prior information.	Formally integrates prior knowledge via the prior distribution.
Output	Point estimates for Vmax and Km.	Full posterior distributions for Vmax and Km, yielding point estimates (e.g., median) and credible intervals.
Uncertainty Quantification	Typically provides confidence intervals based on linear approximations.	Directly quantifies uncertainty from the posterior distribution.
Computational Demand	Low; simple linear algebra.	High; requires iterative sampling algorithms (e.g., MCMC).

Quantitative Analysis of Accuracy and Precision

Simulation studies provide the gold standard for comparing estimation methods, as true parameter values are known. A seminal study [28] simulated progress curves for an enzyme (invertase) and estimated Vmax and Km using five methods under different error conditions. The results, summarized below, demonstrate the clear superiority of direct nonlinear and Bayesian methods.

Table 2: Performance Comparison of Estimation Methods from Simulation Data [28]

Estimation Method	Description	Accuracy (Bias)	Precision (90% CI Width)	Key Limitation
Lineweaver-Burk (LB)	Linear fit to 1/V vs. 1/[S] plot.	Low (High Bias)	Low (Wide CI)	Severe error distortion at low [S].
Eadie-Hofstee (EH)	Linear fit to V vs. V/[S] plot.	Moderate	Moderate	Error in V appears on both axes.
Nonlinear Regression (NL)	Direct nonlinear fit of V to [S].	High (Low Bias)	High (Narrow CI)	Requires good initial estimates.
Nonlinear Differential (NM)	Fit of the full [S]-time progress curve.	Highest (Lowest Bias)	Highest (Narrowest CI)	Computationally intensive; requires full time-course data.

The study found that nonlinear methods (NL, NM) provided the most accurate and precise results. The superiority was most pronounced with a combined (additive + proportional) error model, a realistic scenario in experimental biochemistry where measurement error scales with concentration [28]. The NM method, which fits the integrated rate equation to the entire progress curve, was particularly effective as it utilizes more data points and respects the underlying kinetic model without data transformation [28] [15].

In practical applications, such as analyzing microbial nutrient uptake, Bayesian hierarchical modeling has been successfully used to infer scaling relationships between cell size, Vmax, and Km across diverse organisms, directly quantifying the uncertainty in these allometric parameters [10].

Detailed Experimental and Computational Protocols

Protocol for Traditional Linearization Analysis

This protocol is based on the initial velocity assay.

• Experimental Data Collection: Perform enzyme assays at a minimum of 6-8 different substrate concentrations ([S]), spanning a range from well below to above the expected Km. Record the initial reaction velocity (V) for each [S].
• Data Transformation:
  • For Lineweaver-Burk: Calculate 1/V and 1/[S] for each data point.
  • For Eadie-Hofstee: Calculate V/[S] for each data point.
• Linear Regression: Perform ordinary least squares (OLS) linear regression on the transformed data.
• Parameter Calculation:
  • From Lineweaver-Burk: Y-intercept = 1/Vmax; Slope = Km/Vmax.
  • From Eadie-Hofstee: Y-intercept = Vmax; Slope = -Km.

Protocol for Bayesian Estimation Using Progress Curves

This protocol, adapted from [28] [15], uses the more information-rich progress curve assay.

• Experimental Data Collection: For one or more initial substrate concentrations ([S]0), measure the substrate or product concentration at multiple time points to construct a full progress curve. Experiments can be conducted under different conditions (e.g., varying [S]0 or enzyme concentration) to improve identifiability [15].
• Model Specification:
  • Structural Model: Define the differential equation: d[S]/dt = - (Vmax * [S]) / (Km + [S]).
  • Error Model: Specify a likelihood, e.g., [S]observed ~ Normal([S]predicted, σ²), where σ can be constant (additive) or scale with [S]predicted (proportional/combined).
  • Prior Distributions: Define plausible prior distributions for Vmax, Km, and σ (e.g., Vmax ~ LogNormal(log(1), 1)).
• Posterior Computation:
  • Implement the model in a probabilistic programming language (e.g., Stan, PyMC).
  • Use an MCMC sampler (e.g., NUTS) to draw thousands of samples from the joint posterior distribution of the parameters.
• Diagnostics and Inference:
  • Check MCMC convergence using statistics (R-hat ≈ 1.0) and trace plots.
  • Summarize the posterior samples: report the median and 95% credible interval for Vmax and Km.

Table 3: Research Reagent and Computational Solutions for Kinetic Studies

Item / Tool	Function / Purpose	Key Consideration
Purified Enzyme	The catalyst of interest; source and purity directly impact kinetic constants.	Use consistent batch; document source and purification steps.
Substrate	The molecule transformed by the enzyme; purity is critical.	Ensure solubility across the tested concentration range.
Detection System (Spectrophotometer, Fluorometer, LC-MS)	Measures the depletion of substrate or appearance of product over time.	Linearity of signal with concentration and appropriate temporal resolution are essential.
NONMEM	Industry-standard software for nonlinear mixed-effects modeling (used in [28]).	Powerful for complex population models; steep learning curve.
Stan / PyMC	Probabilistic programming languages for full Bayesian inference.	Flexible, excellent for custom models; requires coding proficiency.
R (nls/mkin) / Python (SciPy)	Environments for standard nonlinear least-squares regression.	Accessible for basic nonlinear fitting; limited in uncertainty quantification.

The evidence strongly favors modern estimation methods over traditional linearization for the accurate and precise determination of Vmax and Km. While linear transformations offer simplicity, they introduce systematic bias and fail to provide reliable uncertainty estimates [28].

Strategic Recommendations:

• For Standard Analysis: Abandon Lineweaver-Burk and Eadie-Hofstee plots in favor of direct nonlinear regression (the NL method). This should be the default approach for fitting initial velocity data.
• For Highest Fidelity: Utilize the progress curve assay coupled with Bayesian estimation (the NM method). This approach makes the most efficient use of experimental data, is robust to various error structures, and provides a complete probabilistic description of parameter uncertainty [28] [15]. It is particularly valuable for characterizing enzymes where conditions deviate from the ideal [E] << Km assumption [15].
• For Complex Problems: Adopt Bayesian hierarchical models when integrating data from multiple sources, incorporating prior literature values, or estimating parameters for a population of enzymes or subjects [10] [83].

The transition from traditional to modern methods represents a shift towards more statistically rigorous, informative, and reproducible kinetic analysis, which is fundamental for advancing research in enzymology and drug development.

The accurate prediction of human hepatic clearance stands as a critical challenge in drug discovery and development. This process determines systemic exposure, influences dosing regimens, and underpins both the efficacy and safety profiles of new chemical entities (NCEs) [84]. At the heart of this predictive endeavor lies the application of enzyme kinetic principles, specifically the estimation of Vmax (maximum reaction velocity) and Km (Michaelis constant, the substrate concentration at half Vmax). These parameters are not merely in vitro measurements; they are fundamental bridges connecting experimental data to in vivo physiological reality.

This whitepaper is framed within a broader thesis positing that robust and accurate estimation of Vmax and Km is the cornerstone of reliable pharmacokinetic prediction. The thesis contends that advancements in estimation methodologies—moving from traditional linearization to modern nonlinear regression and numerical integration—directly enhance our ability to model complex biological systems [28]. This guide will explore how these core parameters are derived, applied in In Vitro to In Vivo Extrapolation (IVIVE), and used to diagnose and manage the clinically critical phenomenon of nonlinear (saturable) pharmacokinetics. Through case studies of classic drugs like phenytoin and ethanol, we will demonstrate the practical implications of these principles for researchers and drug development professionals.

Core Principles: Vmax, Km, and Intrinsic Clearance

The relationship between the rate of an enzyme-mediated reaction (v) and the substrate concentration ([S]) is classically described by the Michaelis-Menten equation: v = (Vmax × [S]) / (Km + [S]) [85] [86].

In pharmacokinetics, this equation is adapted to describe drug elimination, where v represents the rate of metabolism, and [S] is the concentration of unbound drug (Cu). From this, intrinsic clearance (CLint)—the inherent ability of hepatic enzymes to metabolize a drug in the absence of flow or binding limitations—can be defined [85]: CLint = v / Cu = Vmax / (Km + Cu).

The behavior of this system changes dramatically depending on the relationship between drug concentration (Cu) and Km:

• When Cu << Km: The equation simplifies to CLint ≈ Vmax / Km. CLint is constant, and elimination follows first-order kinetics (a constant fraction of drug is eliminated per unit time) [86] [87].
• When Cu >> Km: The equation simplifies to v ≈ Vmax. The metabolic rate approaches a constant maximum, and elimination approximates zero-order kinetics (a constant amount of drug is eliminated per unit time) [86] [87].
• When Cu is close to Km: Nonlinear (mixed-order) kinetics are observed, where clearance is concentration-dependent [85] [88].

Table 1: Key Relationships between Michaelis-Menten Parameters and Pharmacokinetic Behavior

Condition	Simplified Equation	Elimination Kinetics	Clinical Implication
Cu << Km	CLint = Vmax / Km (constant)	First-Order	Predictable, proportional dose-concentration relationship [86].
Cu ≈ Km	CLint = Vmax / (Km + Cu)	Nonlinear (Mixed-Order)	Disproportionate change in concentration with dose adjustment; requires careful monitoring [85].
Cu >> Km	v ≈ Vmax (constant)	Zero-Order (Saturated)	Rate of elimination is constant and limited; risk of accumulation [86] [87].

Diagram 1: Foundational Pathway from Liver to Core Parameters.

Experimental Protocols for Estimating Vmax and Km

Accurate parameter estimation begins with robust in vitro experimental design. The most common systems are human liver microsomes (HLM) and cryopreserved human hepatocytes (CHH), each with distinct advantages [84].

• Microsomal Incubations: Prepared via differential centrifugation of liver homogenate, HLMs are enriched with cytochrome P450 (CYP) and UGT enzymes. They are robust, low-cost, and amenable to high-throughput screening. Assays require addition of cofactors like NADPH [84].
• Hepatocyte Suspensions: Isolated via collagenase digestion, hepatocytes contain a full complement of phase I and II enzymes and transporters, offering a more physiologically complete system. They are crucial for drugs metabolized by non-CYP pathways [84] [89].

The general protocol involves incubating the test compound at various concentrations with the enzyme system (microsomes or hepatocytes) under physiological conditions (pH, temperature). The depletion of the parent compound or formation of metabolite is measured over time (e.g., via LC-MS/MS) to determine reaction velocity (v) at each substrate concentration ([S]) [77].

Parameter Estimation Methodologies

Once [S] vs. v data is obtained, Vmax and Km must be estimated. Traditional methods linearize the Michaelis-Menten equation but have statistical shortcomings [28].

Table 2: Comparison of Vmax and Km Estimation Methods [28]

Method	Plot (y vs. x)	Slope	Y-Intercept	Key Limitations
Lineweaver-Burk	1/v vs. 1/[S]	Km / Vmax	1 / Vmax	Overweights low [S] data, prone to error propagation [28] [77].
Eadie-Hofstee	v vs. v/[S]	-Km	Vmax	Error distribution is not uniform [28].
Hanes-Woolf	[S]/v vs. [S]	1 / Vmax	Km / Vmax	More balanced error distribution than Lineweaver-Burk [86] [77].
Nonlinear Regression (NL)	Direct fit of v vs. [S] to M-M equation	N/A	N/A	Statistically superior; directly fits untransformed data [28].
Numerical Integration (NM)	Fit of [S] vs. time data to differential equation	N/A	N/A	Most accurate; uses full time-course data without velocity approximation [28].

Simulation studies demonstrate that nonlinear regression methods (NL and NM) provide more accurate and precise estimates of Vmax and Km than traditional linearization methods, especially when data contains proportional error [28]. The NM method, which fits the substrate concentration-time profile directly using a differential equation solver (e.g., in NONMEM), is considered the gold standard as it avoids the potentially erroneous calculation of initial velocities [28].

Predicting Human Hepatic Clearance: The IVIVE Framework

The process of In Vitro to In Vivo Extrapolation (IVIVE) translates measured in vitro CLint into a prediction of in vivo hepatic clearance (CLH). This is a three-step process [84]:

• Measure in vitro CLint: Determined from enzyme kinetic (Vmax, Km) or substrate depletion data in HLM or CHH.
• Scale to in vivo CLint: The in vitro value is scaled using a physiological scaling factor.
  • For microsomes: CLint,vivo = CLint,mic × MPPGL × LW, where MPPGL is mg microsomal protein per gram liver, and LW is liver weight.
  • For hepatocytes: CLint,vivo = CLint,hep × HPGL × LW, where HPGL is hepatocellularity (number of cells per gram liver).
• Apply a Liver Model: The scaled CLint is incorporated into a model of hepatic disposition, such as the well-stirred model, which accounts for hepatic blood flow (QH) and unbound fraction in blood (fuB): CLH = (QH × fuB × CLint,vivo) / (QH + fuB × CLint,vivo) [84].

A persistent challenge is the systematic underprediction of in vivo clearance when using biological scaling factors alone. Empirical regression-based scaling factors (e.g., 3- to 9-fold) are often applied to bridge this gap, attributed to factors like loss of enzyme activity during preparation or inadequate representation of all metabolic pathways [89].

Diagram 2: The Three-Step IVIVE Workflow for Clearance Prediction.

Assessment and Implications of Nonlinear Kinetics

Nonlinear kinetics occur when therapeutic drug concentrations approach or exceed the Km of the eliminating enzyme system, leading to saturation. This has profound clinical implications [85].

Diagnosis from Steady-State Data: Nonlinearity is often identified clinically from steady-state concentration (Css) data under different dosing rates (DR). The relationship is described by: DR = (Vmax × Css) / (Km + Css) [86]. A plot of DR vs. Css yields a characteristic "hockey-stick" curve where Css rises disproportionately as DR increases. Vmax and Km can be estimated from this curve using graphical methods (e.g., Lineweaver-Burk, direct linear plot) or by solving simultaneous equations from two different (DR, Css) pairs [86].

Clinical Case Studies

• Phenytoin: The classic example of saturable metabolism within the therapeutic range. With a typical Km of 5 mg/L and Vmax of 450 mg/day, steady-state concentrations rise sharply with small dose increases (e.g., from 300 to 400 mg/day can increase Css from 10 to 40 mg/L) [85]. This necessitates careful therapeutic drug monitoring and small dosage adjustments.
• Ethanol: Exhibits near-zero-order kinetics at typical blood concentrations because its Km (~0.01 g%) is very low. The Vmax (approx. 7-10 g/hour) limits the body's elimination capacity, leading to predictable accumulation upon intake exceeding this constant rate [85] [88].

Table 3: Kinetic Parameters and Clinical Impact of Nonlinear Drugs

Drug	Approximate Km	Approximate Vmax	Therapeutic Range	Clinical Consequence of Nonlinearity
Phenytoin	5 mg/L (total) [85]	450 mg/day [85]	10-20 mg/L [85]	Small dose increases cause large, unpredictable rises in Css; prolonged half-life at high concentrations [85].
Ethanol	0.01 g% (100 mg/L) [85]	7-10 g/hour [85] [88]	N/A	Elimination rate is constant (~1 standard drink/hour); intake above Vmax leads to linear accumulation [85].
Salicylate (High Dose)	Saturation of metabolism & protein binding [85]	-	-	Complex nonlinearity; increased fu leads to non-proportional increase in total Css but linear increase in active, unbound concentration [85].

Diagram 3: Diagnostic Plot for Identifying Nonlinear Kinetics.

Advanced Applications and Recent Advances

The field continues to evolve to address persistent challenges like predicting clearance for low-turnover compounds and integrating more complex biology.

• Addressing Low-Clearance Compounds: Traditional suspension hepatocyte assays are often too brief (<4 hours) to reliably measure the slow depletion of low-CLint drugs. Advanced long-term hepatocyte culture systems, such as HepaSH cell monolayers derived from humanized-liver mice, maintain metabolic function for up to 168 hours. This extended incubation window allows for accurate monitoring and clearance prediction for low-turnover drugs like diazepam and warfarin [90].
• Incorporating Transporter Effects: Recognizing that hepatic clearance is often determined by both metabolism and transport, there is a push to integrate uptake clearance (mediated by transporters like OATP1B1) into IVIVE paradigms for a more holistic prediction [89].
• Modified Michaelis-Menten Equations: For complex scenarios, modifications to the classic equation are applied. For example, accounting for endogenous substrate production (V = (Vmax × S)/(Km + S) + R) [47] or using equations to distinguish enzyme inducers from inhibitors based on their effects on apparent Vmax and Km [47].

Table 4: Advanced Systems for Improved Clearance Prediction

System/Approach	Key Feature	Primary Application	Reference
HepaSH Cell Monolayers	Long-term functional stability (up to 168 hrs) in culture.	Accurate CL prediction for low-turnover compounds [90].	[90]
Co-culture Systems	Hepatocytes cultured with non-parenchymal cells to better maintain phenotype.	Improved metabolic function for extended duration studies.	(Not in search results)
Integrated Transporter-Metabolism Models	Incorporates kinetic parameters for uptake/efflux transporters.	Prediction for compounds where transport is rate-limiting [89].	[89]
Modified M-M Equations	Incorporates terms for endogenous substrates, allosterism, or parallel pathways.	Modeling complex in vivo nonlinear kinetics [47].	[47]

The Scientist's Toolkit: Key Research Reagents and Materials

Table 5: Essential Reagents and Systems for In Vitro Metabolism Studies

Reagent/System	Key Components/Description	Primary Function in Research	Key Considerations
Human Liver Microsomes (HLM)	Membrane vesicles containing CYP, UGT, FMO enzymes.	High-throughput metabolic stability screening, reaction phenotyping, CYP inhibition studies [84].	Requires addition of cofactors (NADPH for CYP); lacks full cellular context and transporters [84].
Cryopreserved Human Hepatocytes (CHH)	Intact primary human liver cells.	Gold standard for intrinsic clearance prediction, studying non-CYP metabolism, and transporter effects [84] [89].	Donor variability; requires pooling for consistency; more complex and costly than HLM [89].
S9 Fraction	Liver homogenate supernatant containing microsomal and cytosolic enzymes.	Broad screening of Phase I and II metabolism in a single system [84].	Less specific than HLM for CYP reactions.
Recombinant CYP Enzymes	Single CYP isoform expressed in a heterologous system.	Reaction phenotyping to identify specific enzymes responsible for metabolism [84].	Non-physiological enzyme levels and lack of natural competition between isoforms.
NADPH Regenerating System	NADP+, glucose-6-phosphate, G6PDH.	Provides essential cofactor for CYP- and FMO-mediated oxidative reactions [84].	Critical for maintaining reaction linearity in microsomal incubations.
UDPGA / Alamethicin	Cofactor for UGTs / pore-forming agent.	Enables assessment of glucuronidation activity in microsomes by allowing substrate access to the luminal UGT active site [84].	Essential for accurate in vitro-in vivo extrapolation of UGT metabolism.
HepaSH Cells	Hepatocytes from chimeric mice with humanized livers, capable of long-term monolayer culture.	Clearance evaluation of low-turnover compounds through extended incubation times (days) [90].	Specialized model requiring specific culture conditions.

The pursuit of understanding enzyme kinetics—quantified by parameters such as the maximum reaction rate (Vmax) and the Michaelis constant (Km)—has traditionally been confined to terrestrial laboratories where gravity is a constant, often overlooked variable. However, the unique environment of microgravity presents a novel paradigm for this foundational biochemical research. By removing gravitational forces, we can isolate and study molecular interactions—such as those between an enzyme and its substrate—free from confounding effects like sedimentation, convection, and density-driven fluid flows [91] [92]. These forces on Earth can mask subtle aspects of diffusion, binding affinity, and allosteric regulation that define Km and Vmax.

This whitepaper posits that microgravity is not merely a novel environment but an essential scientific tool for deconvoluting the fundamental biophysics of enzyme action. Research conducted on the International Space Station (ISS) and commercial platforms reveals that the absence of gravity alters the foundational processes governing drug bioavailability, from the crystalline structure of active pharmaceutical ingredients (APIs) to their dissolution and absorption profiles [93] [94] [92]. Within the specific context of a thesis on Vmax and Km estimation, microgravity experiments offer a unique opportunity to measure these parameters under conditions where transport phenomena are purely diffusion-limited, potentially yielding more precise and intrinsic values. The subsequent sections will detail the physical principles at play, review key experimental findings, and provide a technical framework for designing enzyme kinetics studies in space, directly linking these insights to the development of more effective and stable pharmaceuticals.

Fundamental Microgravity Effects on Molecular and Particulate Systems

The microgravity environment fundamentally alters the physical forces that govern molecular and cellular interactions. The most significant change is the near-elimination of buoyancy-driven convection and sedimentation. On Earth, density differences in fluids—created by temperature gradients or the presence of particles—cause fluid motion that dominates mass transport. In microgravity, this convective mixing is suppressed, leaving molecular diffusion as the primary transport mechanism [92]. This shift from convective-dominant to diffusion-dominant transport has profound implications for any process involving the collision and interaction of molecules or particles, including enzyme-substrate binding and the early stages of crystal nucleation.

Long-term experiments on the ISS have uncovered secondary aggregation mechanisms that become significant in the absence of gravity. A pivotal 99-day study on clay particle flocculation in saline water demonstrated that while Brownian motion is present, the dominant driver for aggregation was low-frequency onboard oscillations, known as g-jitter [91]. These vibrations, originating from machinery, crew activity, and spacecraft maneuvers, induce inertial effects that can accelerate particle collisions beyond rates predicted by diffusion alone. The study found that aggregate growth driven by these oscillations occurred at a faster rate than that caused by Brownian motion, revealing a previously unrecognized mechanism for enhancing molecular and particulate interactions in space [91].

The following table summarizes the key mechanisms affecting particle and molecular interactions in microgravity compared to terrestrial conditions:

Table: Comparative Analysis of Interaction Mechanisms in Terrestrial vs. Microgravity Environments

Interaction Mechanism	Description (Terrestrial)	Description (Microgravity)	Impact on Enzyme/Substrate or Drug Particles
Mass Transport	Dominated by buoyancy-driven convection and sedimentation.	Primarily governed by molecular diffusion; convection is negligible [92].	Slower, more uniform distribution of substrate to enzyme; controlled, diffusion-limited crystal growth.
Particle Aggregation	Governed by gravity-dependent settling, fluid shear, and Brownian motion.	Gravity-dependent settling eliminated; Brownian motion present; g-jitter-induced inertial clustering becomes significant [91].	May enhance encounter frequency between large biomolecular complexes or precipitating crystals.
Crystal Growth & Nucleation	Convection causes irregular solute supply, leading to defects and size dispersion.	Diffusion-limited growth promotes uniform solute delivery, yielding larger, more ordered crystals [93] [92].	Produces high-quality protein crystals for structural analysis; enables uniform API crystals for improved drug formulation.
Fluid Phase Boundaries	Sharp gradients are disrupted by convective mixing.	Stable, predictable diffusion gradients can be established and maintained.	Enables precise study of reaction kinetics within defined concentration fields.

These altered physical conditions create a unique experimental regime. For enzyme kinetics, the diffusion-limited environment means that the measured rate of reaction more directly reflects the intrinsic catalytic efficiency and binding affinity (kcat and Km), as extrinsic factors related to turbulent mixing are minimized. For pharmaceuticals, it allows for the formation of API crystals with unparalleled uniformity and stability, directly impacting dissolution characteristics—a key determinant of bioavailability [95] [92].

Experimental Approaches and Methodologies in Space

Conducting research in microgravity requires specialized hardware, experimental design, and protocols adapted for operation aboard crewed platforms like the ISS or uncrewed commercial capsules. The following sections detail proven methodologies from recent studies.

Protocol for Long-Term Particulate Aggregation Studies

A seminal experiment investigating the long-term aggregation of clay particles in saline water on the ISS provides a template for studying colloidal-scale interactions [91].

• Hardware & Sample Preparation: Ten sample cuvettes were prepared on Earth with defined compositions of kaolinite, montmorillonite, and sand in saline water (35 PSU). Each cuvette contained a magnetic bead for stirring. The cuvettes were installed in the Binary Colloidal Alloy Test (BCAT) rack within the Japanese Experiment Module (JEM) [91].
• In-Space Protocol: Upon arrival at the ISS, an astronaut used an external magnet to swirl the internal bead for 60 seconds per cuvette to homogenize the suspension. The samples were then left undisturbed for 99 days. A Nikon D2Xs camera with remote shutter release captured images at intervals ranging from every 30 minutes initially to every 4 hours by the experiment's end [91].
• Data Collection & Analysis: Two accelerometers (Space Accelerometer Measurement System - SAMS) co-located in the JEM recorded g-jitter vibrations. Image analysis used an autocorrelation function on the grayscale pixel intensity of 2D images to quantify the mean floc size over time [91].

Protocol for Pharmaceutical Stability Testing

NASA's Exploration Medical Capability (ExMC) Element executed a rigorous ground-based study simulating space radiation effects on drug stability, a protocol readily adaptable for in-space validation [96].

• Sample Selection & Grouping: Four solid oral medications (Acetaminophen, Amoxicillin, Ibuprofen, Promethazine) were selected. Identical lots were assigned to four groups: a non-irradiated control, a traveling control, and two irradiation groups exposed to simulated Galactic Cosmic Radiation (GCRSim) at 0.5 Gy and 1.0 Gy [96].
• Irradiation & Storage: Irradiation was performed at the NASA Space Radiation Laboratory (NSRL). All samples, including controls, subsequently underwent a 34-month storage period under controlled temperature conditions [96].
• Stability Assessment: At 2, 18, and 34 months, samples were analyzed for: 1) Active Pharmaceutical Ingredient (API) content via HPLC/UPLC, 2) Degradation impurities, and 3) Dissolution rate. Stability was assessed against United States Pharmacopeia (USP) acceptance criteria [96].

Workflow for Space-Based Enzyme Kinetics Studies

Synthesizing the principles from the above protocols and commercial biotech approaches, a generalized workflow for a microgravity enzyme kinetics experiment can be formulated.

Diagram: Integrated workflow for conducting enzyme kinetics and crystallization experiments in microgravity, from terrestrial design to post-flight analysis.

Implications for Pharmaceutical Bioavailability and Drug Development

The altered physical processes in microgravity have direct, translatable consequences for pharmaceutical science, particularly in areas defining drug bioavailability: API crystal form, dissolution rate, and formulation stability.

Enhanced Crystallization for Improved Formulations

Microgravity enables the growth of higher-quality protein and small-molecule crystals. The commercial case is exemplified by Merck’s research on pembrolizumab (Keytruda) aboard the ISS. Microgravity crystallization produced uniform 39-micrometer particles, a stark contrast to the irregular 13–102 micrometer range observed in Earth-grown crystals [95]. This uniformity is critical for reformulating the drug from intravenous (IV) infusion to a subcutaneous injection, which can improve patient convenience and reduce healthcare system costs by an estimated 50-71% per treatment [95]. Varda Space Industries has replicated this approach on uncrewed platforms, demonstrating that microgravity provides "more control over particle size and make[s] the content of drug products more uniform" [92].

Drug Stability in the Space Environment

A primary concern for long-duration missions is the stability of pharmaceuticals. A comprehensive NASA study exposed four common medications (Acetaminophen, Amoxicillin, Ibuprofen, Promethazine) to simulated galactic cosmic radiation (up to 1.0 Gy) followed by long-term storage [96]. The key finding was that ionizing radiation at mission-relevant doses did not accelerate the degradation of the solid oral APIs beyond control levels. All samples met USP potency standards throughout the 34-month study [96]. This suggests that for many solid formulations, radiation during multi-year missions may not be a primary destabilizing factor, though non-solid formulations and specific radiation-sensitive compounds require further study.

Modeling Complex Biological Responses

Beyond crystallization, microgravity enables advanced biological modeling. The NIH’s Tissue Chips in Space program uses microfluidic devices containing living human cells to model organ-level physiology. In microgravity, cells assemble into more natural, 3D structures, providing superior models for studying disease mechanisms, aging (which appears accelerated in space), and drug responses [93] [94]. Furthermore, studies on the combined effects of microgravity and radiation reveal complex cellular interplay. One study found that while radiation increased genomic instability in directly exposed target cells, low-dose radiation in a microgravity environment could trigger protective signaling to bystander cells, reducing their risk of carcinogenic transformation [97]. This nuanced understanding of combined space stressors is vital for developing effective countermeasures for astronauts and may inform new terrestrial cancer therapies.

Table: Key Commercial and Research Outcomes from Microgravity Pharmaceutical Studies

Company/Initiative	Drug/Technology	Microgravity Outcome	Terrestrial Application & Impact
Merck	Pembrolizumab (Keytruda)	Production of uniform, ~39 µm crystals [95].	Enables reformulation from IV to subcutaneous injection; potential for patent extension and significant market advantage [93] [95].
Varda Space Industries	Ritonavir & other APIs	Demonstration of orbital crystallization and successful Earth return on uncrewed platforms [92].	Pathfinding for scalable orbital manufacturing of improved drug formulations [92].
NASA/NIH Tissue Chips	Various disease models	Enhanced 3D tissue morphogenesis and function in microgravity [93] [94].	Improved preclinical models for disease study and drug testing, potentially reducing late-stage trial failures.
LambdaVision	Artificial retina	Layer-by-layer protein deposition with unprecedented uniformity [95].	Development of a bioengineered implant to treat degenerative retinal diseases.
NASA ExMC	Common solid oral medications	Confirmed stability of APIs after simulated space radiation exposure [96].	Informs medical kit planning for Artemis and Mars missions; assures crew medication efficacy.

The Scientist's Toolkit: Key Platforms and Reagents

Conducting research in microgravity relies on specialized platforms, both for creating the environment and for executing experiments.

Table: Essential Platforms and Reagents for Microgravity Life Sciences Research

Tool/Platform	Function	Example Use in Research
International Space Station (ISS) & Commercial Stations	Provides sustained microgravity environment; hosts laboratory racks (e.g., JEM, Destiny module).	Hosts the BCAT rack for colloidal science [91], BioFabrication Facility for 3D bioprinting [95], and commercial incubators.
Binary Colloidal Alloy Test (BCAT) Hardware	Sample cuvettes and imaging system designed for long-term observation of colloidal phase changes [91].	Used for 99-day clay aggregation study to monitor floc size via time-lapse photography [91].
Microfluidic Tissue Chips	Miniaturized devices that support living human cells in channeled, perfused environments.	NIH's Tissue Chips in Space program to model organ-level disease and drug response [93] [94].
Hypergravity Crystallization Platform	A large-diameter centrifuge used on Earth to test an API's sensitivity to gravity gradients (1g to 5g) [92].	Varda uses this to screen and validate which APIs are likely to benefit from microgravity crystallization before launch [92].
Space Accelerometer Measurement System (SAMS)	Suite of sensors that measure and record vibrational accelerations (g-jitter) on the ISS [91].	Characterizes the low-frequency oscillation environment that can drive particle aggregation in experiments [91].
Dried Blood Spot (DBS) / Dried Urine Spot (DUS)	Minimally invasive bio-sampling technique requiring small volumes and no refrigeration [98].	Enables pharmacokinetic (PK) studies in space to monitor astronaut drug metabolism [98].

Technical Research Guide: Integrating Enzyme Kinetics into Microgravity Studies

For researchers aiming to integrate Vmax and Km estimation into microgravity investigations, the following technical guide outlines critical considerations.

Defining the Research Hypothesis

Link the microgravity environment directly to a kinetic parameter. Example hypotheses include:

• "The elimination of convective transport in microgravity will reduce the apparent Km for a diffusion-limited enzyme-substrate pair, revealing a lower, more intrinsic binding constant."
• "G-jitter-induced inertial effects will increase the effective collision frequency of large, multi-subunit enzyme complexes with their substrates, leading to an increase in apparent Vmax compared to diffusion-only ground models."

Designing the Experimental Payload

• Enzyme Immobilization: Use covalent immobilization on a surface within a flow chamber. This mimics the microscale steady-state kinetic analysis (microSKA) approach [99] and is ideal for spaceflight, as it eliminates sedimentation of the enzyme and allows precise control of substrate delivery.
• Substrate Delivery & Mixing: Employ a diffusion-dominated microfluidic system. Without convection, use slow, controlled flow or stopped-flow methods to establish stable, calculable diffusion gradients of substrate toward the immobilized enzyme bed.
• Real-Time Detection: Incorporate optical detection (e.g., fluorescence, absorbance) within the payload. Monitoring product formation as a function of position along a flow chamber (as in microSKA) [99] or time in a stopped-flow cell is essential, as sample return may be delayed.

Controlling for the Microgravity Environment

• 1g In-Flight Controls: If possible, include an on-board centrifuge to run a parallel 1g control within the same spacecraft environment. This directly isolates the gravity variable from other spaceflight factors (e.g., radiation, vibration).
• Ground Controls: Conduct identical experiments in terrestrial labs, but use gelled or viscous media to attempt to mimic diffusion-limited conditions for comparison.
• Monitor g-Jitter: Request SAMS data or include a low-cost accelerometer in your payload to correlate any anomalous kinetic data with specific vibration events [91].

Data Analysis and Interpretation

• Modeling Diffusion-Limited Kinetics: Adapt kinetic models to account for a diffusion-limited substrate supply. The observed rate will be a function of both the intrinsic enzyme kinetics (Vmax, Km) and the substrate flux.
• Comparing Parameters: Statistically compare derived Vmax and Km values from spaceflight experiments with those from 1g in-flight and ground controls. Significance would indicate a direct or indirect gravity-dependence of the enzymatic mechanism.

By following this structured approach, researchers can rigorously test how gravitational force influences the most fundamental parameters of enzyme action, contributing valuable data to both basic biochemistry and the applied science of drug development in space.

Conclusion

Accurate estimation of Vmax and Km is fundamental to understanding enzyme behavior, with direct implications for drug discovery, metabolic prediction, and clinical pharmacology. This synthesis highlights that while foundational Michaelis-Menten principles and classical linearization methods remain essential, modern approaches—such as nonlinear regression, Bayesian inference using the tQSSA model, and optimized experimental designs—significantly enhance reliability, especially under complex conditions like high enzyme concentrations. Future directions should focus on integrating these advanced models into routine practice, exploring environmental factors like microgravity on drug kinetics, and leveraging high-throughput data for model-informed drug development to improve the prediction of in vivo outcomes and personalized therapeutic strategies.

References

• 1. What Is Enzyme Kinetics? Understanding Km and Vmax in ... [https://synapse.patsnap.com/article/what-is-enzyme-kinetics-understanding-km-and-vmax-in-biochemical-reactions]
• 2. Enzyme Kinetics - Structure - Function - Michaelis-Menten ... [https://teachmephysiology.com/biochemistry/molecules-and-signalling/enzyme-kinetics/]
• 3. Catalytic Efficiency of Enzymes [https://chem.libretexts.org/Bookshelves/Biological_Chemistry/Supplemental_Modules_(Biological_Chemistry)/Enzymes/Enzymatic_Kinetics/Catalytic_Efficiency_of_Enzymes]
• 4. Mechanistic Interpretation of Conventional Michaelis ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4204736/]
• 5. Michaelis-Menten Kinetics [https://chem.libretexts.org/Bookshelves/Biological_Chemistry/Supplemental_Modules_(Biological_Chemistry)/Enzymes/Enzymatic_Kinetics/Michaelis-Menten_Kinetics]
• 6. 5.2: Enzyme Parameters [https://chem.libretexts.org/Courses/University_of_Arkansas_Little_Rock/CHEM_4320_5320%3A_Biochemistry_1/05%3A_Michaelis-Menten_Enzyme_Kinetics/5.2%3A_Enzyme_Parameters]
• 7. Kinetic Parameters Vmax Km → Area → Resource 1 [https://energy.sustainability-directory.com/area/kinetic-parameters-vmax-km/resource/1/]
• 8. Parameter Reliability and Understanding Enzyme Function [https://pmc.ncbi.nlm.nih.gov/articles/PMC8746786/]
• 9. Optimized Experimental Design for the Estimation of ... [https://www.sciencedirect.com/science/article/abs/pii/S0090955624061786]
• 10. Linking Cell Size, Vmax and Km in Phototrophs ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12178613/]
• 11. Translation of the 1913 Michaelis-Menten Paper - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC3381512/]
• 12. Michaelis–Menten kinetics [https://en.wikipedia.org/wiki/Michaelis%E2%80%93Menten_kinetics]
• 13. 7.2: Derivation of Michaelis-Menten equation [https://bio.libretexts.org/Courses/Wheaton_College_Massachusetts/Principles_of_Biochemistry/07%3A_Enzymes_catalysis_and_kinetics/7.02%3A_Derivation_of_Michaelis-Menten_equation]
• 14. A guide to the Michaelis-Menten equation: steady state and ... [https://pubmed.ncbi.nlm.nih.gov/34270860/]
• 15. Beyond the Michaelis-Menten equation: Accurate and ... [https://www.nature.com/articles/s41598-017-17072-z]
• 16. Investigating the Impact of Temperature and pH on Enzyme ... [https://www.omicsonline.org/open-access/investigating-the-impact-of-temperature-and-ph-on-enzyme-activity-a-kinetic-analysis-135969.html]
• 17. Enzyme Parameters and Michaelis-Menten Plots [https://www.sketchy.com/mcat-lessons/enzyme-parameters-and-michaelis-menten-plots]
• 18. Michaelis Menten Kinetics – MCAT Biochemistry [https://www.medschoolcoach.com/michaelis-menten-kinetics-mcat-biochemistry/]
• 19. Vmax - Definition and Examples - Biology Online Dictionary [https://www.biologyonline.com/dictionary/vmax]
• 20. 10.2: The Equations of Enzyme Kinetics [https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Physical_Chemistry_for_the_Biosciences_(LibreTexts)/10%3A_Enzyme_Kinetics/10.02%3A_The_Equations_of_Enzyme_Kinetics]
• 21. What is the significance of the hyperbolic and sigmoidal ... [https://www.atlas.org/solution/79a076a4-253d-4397-93a3-d7b8cb562990/what-is-the-significance-of-the-hyperbolic-and-sigmoidal-curves-in-understanding-enzyme-behavior]
• 22. Mastering Lineweaver-Burk Plots: A Comprehensive Guide ... [https://www.2minutemedicine.com/mastering-lineweaver-burk-plots-a-comprehensive-guide-for-mcat-biochemistry/]
• 23. 2.7.2: Enzyme Active Site and Substrate Specificity [https://bio.libretexts.org/Bookshelves/Microbiology/Microbiology_(Boundless)/02%3A_Chemistry/2.07%3A_Enzymes/2.7.02%3A__Enzyme_Active_Site_and_Substrate_Specificity]
• 24. Enzyme Substrate Complex - an overview [https://www.sciencedirect.com/topics/medicine-and-dentistry/enzyme-substrate-complex]
• 25. Biochemistry, Proteins Enzymes - StatPearls - NCBI Bookshelf [https://www.ncbi.nlm.nih.gov/books/NBK554481/]
• 26. Enzyme Dynamics: Capturing enzymes in motion [https://elifesciences.org/articles/108727]
• 27. 3.6: Steady State Approximation [https://chem.libretexts.org/Courses/Johns_Hopkins_University/030.356_Advanced_Inorganic_Laboratory/03%3A_Lab_EF-_Chemical_Kinetics/3.06%3A_Steady_State_Approximation]
• 28. Comparison of various estimation methods for the ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6989224/]
• 29. Enzyme specificity prediction using cross-attention graph ... [https://www.nature.com/articles/s41586-025-09697-2]
• 30. Illuminating the universe of enzyme catalysis in the era ... [https://www.sciencedirect.com/science/article/abs/pii/S2405471225002054]
• 31. Basics of Enzymatic Assays for HTS - NCBI - NIH [https://www.ncbi.nlm.nih.gov/sites/books/NBK92007/]
• 32. Uses and misuses of progress curve analysis in enzyme ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2701647/]
• 33. Relationship between enzyme concentration and Michaelis ... [https://www.sciencedirect.com/science/article/abs/pii/S0300908420301346]
• 34. Analytical and numerical approaches to the analysis of ... [https://www.sciencedirect.com/science/article/pii/S1359511325000376]
• 35. Lineweaver–Burk plot [https://en.wikipedia.org/wiki/Lineweaver%E2%80%93Burk_plot]
• 36. Enzyme Kinetics - an overview [https://www.sciencedirect.com/topics/pharmacology-toxicology-and-pharmaceutical-science/enzyme-kinetics]
• 37. 4.10: Lineweaver-Burk Plots [https://bio.libretexts.org/Bookshelves/Biochemistry/Book%3A_Biochemistry_Free_and_Easy_(Ahern_and_Rajagopal)/04%3A_Catalysis/4.10%3A_Lineweaver-Burk_Plots]
• 38. Eadie–Hofstee diagram [https://en.wikipedia.org/wiki/Eadie%E2%80%93Hofstee_diagram]
• 39. Eadie-Hofstee Plot Definition - Biological Chemistry II [https://fiveable.me/key-terms/biological-chemistry-ii/eadie-hofstee-plot]
• 40. Hanes-Woolf Plot Definition - Biological Chemistry II [https://fiveable.me/key-terms/biological-chemistry-ii/hanes-woolf-plot]
• 41. IT+BT，罗小舟课题组揭秘酶催化常数预测的“黑科技”！ - 合成所 [https://isynbio.siat.ac.cn/siat/2025-02/14/article_2025021400542622810.html]
• 42. Use of nonlinear regression to analyze enzyme kinetic data [https://pubmed.ncbi.nlm.nih.gov/2327571/]
• 43. Current statistical methods for estimating the Km and Vmax ... [https://www.sciencedirect.com/science/article/pii/S0307441296000891]
• 44. Comparison of various estimation methods ... [https://synapse.koreamed.org/articles/1094566]
• 45. Maximum Reaction Velocity - an overview [https://www.sciencedirect.com/topics/immunology-and-microbiology/maximum-reaction-velocity]
• 46. 6 Optimization | Building Skills in Quantitative Biology [https://www.quantitative-biology.ca/optimization.html]
• 47. Application of modified Michaelis – Menten equations for ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8507113/]
• 48. Microsomal prediction of in vivo clearance of CYP2C9 ... [https://pubmed.ncbi.nlm.nih.gov/10383540/]
• 49. The Multiple Depletion Curves Method Provides Accurate ... [https://www.sciencedirect.com/science/article/abs/pii/S0090955624019020]
• 50. Application of modified Michaelis – Menten equations for ... [https://bmcpharmacoltoxicol.biomedcentral.com/articles/10.1186/s40360-021-00521-x]
• 51. The multiple depletion curves method provides accurate ... [https://pubmed.ncbi.nlm.nih.gov/18824525/]
• 52. Importance of Observing the Progress Curve During Enzyme Assay in an Automated Clinical Chemistry Analyzer: A Case Study - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC9092719/]
• 53. MCAT Enzyme Kinetics: Km and Vmax Explained [https://www.inspiraadvantage.com/blog/mcat-enzyme-kinetics-km-vmax-explained]
• 54. Basics of Enzymatic Assays for HTS - Assay Guidance Manual - NCBI Bookshelf [https://www.ncbi.nlm.nih.gov/books/NBK92007/]
• 55. Enzymes Purity Analysis [https://diagnostic-enzymes.creative-enzymes.com/enzymes-purity-analysis.html]
• 56. Validating Identity, Mass Purity and Enzymatic ... [https://pubmed.ncbi.nlm.nih.gov/22553867/]
• 57. 5.4: Enzyme Inhibition [https://chem.libretexts.org/Courses/University_of_Arkansas_Little_Rock/CHEM_4320_5320%3A_Biochemistry_1/05%3A_Michaelis-Menten_Enzyme_Kinetics/5.4%3A_Enzyme_Inhibition]
• 58. Cytochrome P450 Enzyme Kinetics: Km and Vmax Determinations Using Metabolite Formation and Substrate Depletion Methods | SpringerLink [https://link.springer.com/protocol/10.1007/978-1-0716-1542-3_5]
• 59. A General Guide for the Optimization of Enzyme Assay ... [https://www.sciencedirect.com/science/article/pii/S247255522206779X]
• 60. Enzyme kinetics [https://en.wikipedia.org/wiki/Enzyme_kinetics]
• 61. Optimizing Substrate Concentrations for Accurate Turnover ... [https://synapse.patsnap.com/article/optimizing-substrate-concentrations-for-accurate-turnover-rate-measurements]
• 62. Importance of study design for estimation of Vmax and Km ... [https://www.page-meeting.org/Abstracts/importance-of-study-design-for-estimation-of-vmax-and-km-characterising-nonlinear-monoclonal-antibody-clearance/]
• 63. Notebook Future: Enzyme Testing | LYON - iGEM 2025 [https://2025.igem.wiki/lyon/notebook_future]
• 64. Guide to Enzyme Unit Definitions and Assay Design [https://resources.biomol.com/biomol-blog/guide-to-enzyme-unit-definitions-and-assay-design]
• 65. Advanced Assay Development Guidelines for Image-Based ... [https://www.ncbi.nlm.nih.gov/books/NBK126174/]
• 66. Rigorous Analysis of the Quasi-Steady-State Assumption in ... [https://www.mdpi.com/2227-7390/10/7/1086]
• 67. Modeling Networks of Coupled Enzymatic Reactions Using ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC1828705/]
• 68. Validity of the total quasi-steady-state approximation in ... [https://arxiv.org/abs/2503.00776]
• 69. A Deep Learning-Based Approach for Predicting Michaelis ... [https://www.mdpi.com/2076-3417/15/7/4017]
• 70. and the Michaelis-Menten Constant (3.2.6) | CIE... | TutorChase Vmax [https://www.tutorchase.com/notes/cie-a-level/biology/3-2-6-vmax-and-the-michaelis-menten-constant]
• 71. Video: Determination of Michaelis Constant and Maximum Elimination... [https://www.jove.com/science-education/v/16601/determination-of-michaelis-constant-and-maximum-elimination-rate]
• 72. Optimal Experimental Design for Assessment of Enzyme ... [https://www.sciencedirect.com/science/article/abs/pii/S0090955624057611]
• 73. Optimized experimental design for the estimation of ... [https://pubmed.ncbi.nlm.nih.gov/22942316/]
• 74. Optimal Experimental Design for Assessment of Enzyme ... [https://pubmed.ncbi.nlm.nih.gov/21289074/]
• 75. Optimal experimental design for assessment of enzyme ... [http://kau.diva-portal.org/smash/record.jsf?pid=diva2:358255]
• 76. Optimizing enzyme inhibition analysis: precise estimation ... [https://www.nature.com/articles/s41467-025-60468-z]
• 77. How to Determine and Km from Lab Data Vmax [https://synapse.patsnap.com/article/how-to-determine-km-and-vmax-from-lab-data]
• 78. Inhibitory Effects of Bisphenol Z on 11β-Hydroxysteroid ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12525740/]
• 79. MLAGO: machine learning-aided global optimization for Michaelis... [https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-022-05009-x]
• 80. Improving generalization ability of deep-learning-based ... [https://www.nature.com/articles/s44387-025-00026-6]
• 81. Numerical PDE solvers outperform neural ... [https://arxiv.org/html/2507.21269v1]
• 82. Machine Learning Prediction and Validation of Plasma ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12135056/]
• 83. Bayesian Statistics: A Modern Data Analysis in 2025 [https://clinilaunchresearch.in/guide-to-bayesian-statistics/]
• 84. Successful and Unsuccessful Prediction of Human Hepatic ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8504179/]
• 85. Pharmacokinetics made easy 9: Non-linear pharmacokinetics [https://australianprescriber.tg.org.au/articles/pharmacokinetics-made-easy-9-non-linear-pharmacokinetics.html]
• 86. Michaelis Menten Equation - Nonlinear Pharmacokinetics [https://www.pharmacy180.com/article/michaelis-menten-equation-2530/]
• 87. Non-linear PK - Professor Emeritus Nick Holford [https://holford.fmhs.auckland.ac.nz/teaching/medsci719/workshops/nonlinearpk/]
• 88. First order, zero order and non-linear elimination kinetics [https://derangedphysiology.com/main/cicm-primary-exam/pharmacokinetics/Chapter-337/first-order-zero-order-and-non-linear-elimination-kinetics]
• 89. Prediction of Hepatic Clearance in Human From In Vitro ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2691463/]
• 90. Prediction of Human Hepatic Clearance with HepaSH ... [https://www.sciencedirect.com/science/article/pii/S009095562509511X]
• 91. Long-term microgravity experiments reveal a new ... [https://www.nature.com/articles/s41526-025-00523-7]
• 92. Crystallizing the Future [https://themedicinemaker.com/issues/2025/articles/aug/crystallizing-the-future/]
• 93. Drug Development in Microgravity: The Next Frontier ... [https://itif.org/publications/2025/05/27/drug-development-in-microgravity-the-next-frontier-in-biopharmaceutical-innovation/]
• 94. Emergence of a New Era for Pharmaceutical Industry [https://pubmed.ncbi.nlm.nih.gov/40826996/]
• 95. Space Biotech as a Strategic Advantage in 2025 and Beyond [https://spaceinsider.tech/2025/08/12/space-biotech-as-a-strategic-advantage-why-early-movers-stand-to-win-billions/]
• 96. The long-term stability of solid-state oral pharmaceuticals ... [https://www.nature.com/articles/s41526-025-00469-w]
• 97. Microgravity alleviates low-dose radiation-induced non ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12174362/]
• 98. Pharmaceutical and biomedical challenges for crew autonomy ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12508180/]
• 99. Measurement of enzyme kinetics using microscale steady- ... [https://pubmed.ncbi.nlm.nih.gov/15248725/]